初中数学北师大版八年级上册3 平行线的判定完美版课件ppt

这是一份初中数学北师大版八年级上册3 平行线的判定完美版课件ppt，共30页。PPT课件主要包含了导入新知，素养目标，探究新知，几何语言，∴∠7∠3，∴AB∥CD，对顶角相等，等量代换，AB∥CD，巩固练习等内容，欢迎下载使用。

2. 能根据“同位角相等，两直线平行”证明“内错角相等，两直线平行”，“同旁内角互补，两直线平行” 并能简单地应用这些结论
1. 初步了解证明的基本步骤和书写格式.
3. 能够根据平行线的判定方法进行简单的推理.
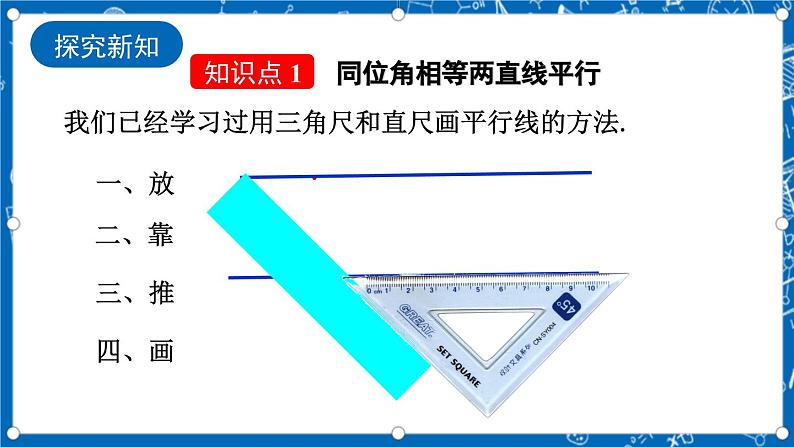
我们已经学习过用三角尺和直尺画平行线的方法.
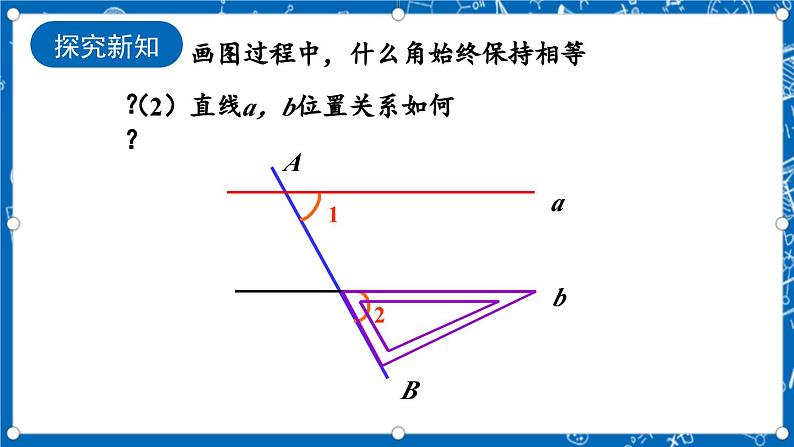
（1）画图过程中，什么角始终保持相等？
（2）直线a，b位置关系如何？
（3）将其最初和最终的两种特殊位置抽象成几何图形：
(4) 由上面的操作过程，你能发现判定两直线平行的方法吗？
判定方法1：两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成：同位角相等，两直线平行.
∵∠1=∠2∴l1∥l2
（同位角相等，两直线平行）.
例 下图中，如果∠1=∠7，能得出AB∥CD吗？写出你的推理过程.
解：∵∠1=∠7 ∠1=∠3
（ ）,
（ ）.
（ ）.
同位角相等两直线平行
利用同位角相等判定两直线平行
如图所示，∠1＝∠2＝35°，则AB与CD的关系是 ，理由是 .
同位角相等，两直线平行
定理 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.这个定理可以简单说成:内错角相等,两直线平行.
你能运用所学知识来证实它是一个真命题吗?
已知: 如图,∠1和∠2是直线a,b被直线c截出的内错角,且∠1=∠2.求证: a∥b.
证明:∵ ∠1=∠2 ,
∠1=∠3 ,
(同位角相等,两直线平行)
判定方法2：两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成：内错角相等，两直线平行.
∵∠3=∠2(已知)∴a∥b (内错角相等，两直线平行)
例 完成下面证明：如图所示，CB平分∠ACD，∠1＝∠3. 求证AB∥CD. 证明：∵CB平分∠ACD，∴∠1＝∠2( ).∵∠1＝∠3，∴∠2＝∠ . ∴AB∥CD( ).
内错角相等，两直线平行
利用内错角相等判定两直线平行
已知∠3=45 °，∠1与∠2互余，试说明AB//CD ？
解：∵∠1=∠2（对顶角相等）， ∠1与∠2互余， ∴ ∠1+∠2=90°(已知). ∴∠1=∠2=45°. ∵ ∠3=45°(已知), ∴∠ 2=∠3. ∴ AB∥CD(内错角相等，两直线平行).
两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行. 条件是： ，结论是： .
利用同旁内角互补判定两直线平行
已知: 如图,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补.求证: a∥b.
证明: ∵ ∠1与∠2互补
∴∠1+∠2=1800
又∵∠3+∠1=1800
∴∠2=∠3
∴ a∥b
(同位角相等,两直线平行).
判定方法3：两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成：同旁内角互补，两直线平行.
∵∠1+∠2=180°(已知),∴a∥b（同旁内角互补，两直线平行）.
例 如图：直线AB、CD都和AE相交，且∠1+∠A=180º ．求证：AB//CD.
证明：∵∠1+∠A=180º
∴∠2+∠A=180º
（ ）,
（ ）.
（ ）.
同旁内角互补，两直线平行
∠1=∠2 （ ）,
① ∵ ∠2 = ∠ 6（已知）, ∴ ___∥___( ).
② ∵ ∠3 = ∠5（已知）, ∴ ___∥___( ).
③∵ ∠4 +___=180（已知）, ∴ ___∥___( ).
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
根据条件完成填空.
蜂房的底部由三个全等的四边形围成，每个四边形的形状如右图所示，其中∠α=109°28′,∠β=70°32′,试确定这三个四边形的对边的位置关系，并说明你的理由.
答：这三个四边形的对边分别平行，因为∠α+∠β=180°,根据同旁内角互补，两直线平行.
结合图，用符号语言表达定理“同旁内角互补，两直线平行”的推理形式：∵___________________，∴a∥b．
1.如图,可以确定AB∥CE的条件是( )A.∠2=∠BB. ∠1=∠AC. ∠3=∠BD. ∠3=∠A
2.如图,已知∠1=30°,∠2或∠3满足条件 ，则a//b.
∠2＝150°或∠3＝30°
3.如图.（1）从∠1=∠4，可以推出　 ∥ ， 理由是__________________________.
（2）从∠ABC +∠ =180°，可以推出AB∥CD ，理由是 .
(3)从∠ =∠ ，可以推出AD∥BC，理由是 _____________________ .
(4)从∠5=∠ ，可以推出AB∥CD， 理由是____________ .
① ∵ ∠1 =____（已知）, ∴ AB∥CE( ).
② ∵ ∠1 +_____=180（已知）, ∴CD∥BF( ).
③ ∵ ∠1 +∠5 =180（已知）, ∴ ___∥_____( ).
④ ∵ ∠4 +_____=180（已知） ∴ CE∥AB( )
4.根据条件完成填空.
理由如下： ∵ AC平分∠DAB（已知）, ∴ ∠1=∠2（角平分线定义）. 又∵ ∠1= ∠3（已知）, ∴ ∠2=∠3（等量代换）. ∴ AB∥CD(内错角相等，两直线平行).
如图，已知∠1= ∠3，AC平分∠DAB，你能判断哪两条直线平行？请说明理由？
∴ AB∥MN（内错角相等，两直线平行）.
∵ ∠MCA= ∠ A（已知）,
又 ∵∠ DEC= ∠ B（已知）,
∴ AB∥DE（同位角相等，两直线平行）.
∴ DE∥MN（如果两条直线都和第三条直线平行，那 么这两条直线也互相平行）.
如图，已知∠MCA= ∠ A， ∠ DEC= ∠ B，那么DE∥MN吗？为什么？