2022八年级数学上学期期中综合训练新版新人教版

这是一份2022八年级数学上学期期中综合训练新版新人教版，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
期中综合训练一、选择题1.下面四个美术字中可以看作轴对称图形的是(　　)2.下列长度的三条线段,能组成三角形的是(　　)A.4 cm,5 cm,9 cm B.8 cm,8 cm,15 cmC.5 cm,5 cm,10 cm D.6 cm,7 cm,14 cm3.已知等腰三角形的一个外角为130°,则这个等腰三角形的顶角为(　　)A.80° B.50°C.80°或65° D.80°或50°4.如图,△ABC的角平分线AD、中线BE相交于点O,则:①AO是△ABE的角平分线;②BO是△ABD的中线;③DE是△ADC的中线;④ED是△EBC的角平分线.其中正确的有(　　)A.1个 B.2个 C.3个 D.4个5.如图,AC是线段BD的垂直平分线,则图中全等三角形的对数是(　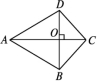　)A.1 B.2 C.3 D.46.在平面直角坐标系中,若点P(-20,a)与点Q(b,13)关于y轴对称,则a+b的值为(　　)A.33 B.-33 C.-7 D.77.如图,在△ABC中,∠BAC=90°,∠C=30°,AD⊥BC于点D,BE是∠ABC的平分线,且交AD于点P,交AC于点E.如果AP=2,那么AC的长为(　　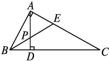)A.8 B.6 C.4 D.28.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是(　　)A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC9.如图,A,B,C三点在同一条直线上,∠A=52°,BD是AE的垂直平分线,垂足为点D,则∠EBC的度数为(　　)A.52° B.76° C.104° D.128°10.如图,过边长为1的等边三角形ABC的边AB上的一点P作PE⊥AC于点E,Q为BC的延长线上一点.当PA=CQ时,连接PQ交AC边于点D,则DE的长为(　　)A. B. C. D.不能确定二、填空题11.若三角形的一个外角等于和它相邻的内角的4倍,等于与它不相邻的一个内角的2倍,则此三角形各内角的度数是　　　　　　　　　　　. 12.如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC的长是　　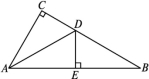　　　. 13.已知等腰三角形的两边长a,b满足|a-b-2|+=0,则此等腰三角形的周长为　　　　　　.14.如图,在△ABC中,∠B=90°,AC=DC,∠D=15°,AB=18 cm,则CD的长为　　　　　cm. 15.如图,在4×4的正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数是　　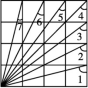　　　. 16.如图,在四边形ABDC中,∠A=110° ,若点D在AB,AC的垂直平分线上,则∠BDC的度数为　　　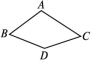　　. 三、解答题17.如图,在△ABC中,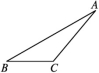(1)画出BC边上的高AD和中线AE;(2)若∠B=30°,∠ACB=130°,求∠BAD和∠CAD的度数.           18.△ABC在平面直角坐标系中如图所示,其中点A,B,C的坐标分别为(-2,1),(-4,5),(-5,2).(1)作△ABC关于直线l:x=-1对称的△A1B1C1,其中,点A,B,C的对应点分别为A1,B1,C1;(2)写出点A1,B1,C1的坐标.             19.如图,在△ABC中,AB=AC,∠BAC=120° ,AD是BC边上的中线,且BD=BE,计算∠ADE的度数.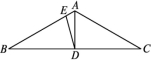         20.两个大小不同的等腰直角三角尺如图①所示放置,图②是由它抽象出的几何图形,点B,C,E在同一条直线上,连接DC.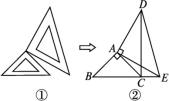(1)请找出图②中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)证明:DC⊥BE.      21.如图,在△ABC中,AB=AC,点D,E分别在AC,AB上,BD=BC,AD=DE=BE,求∠A的度数. 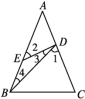    22.如图,已知D,E,F分别是△ABC三边上的点,BF=CE,且△DBF和△DCE的面积相等.求证:AD平分∠BAC.     23.如图①,②,③,点E,D分别是等边三角形ABC,正方形ABCM,正五边形ABCMN中以点C为顶点的相邻两边上的点,且BE=CD,DB交AE于点P.(1)图①中,∠APD的度数为　　　　　; (2)图②中,∠APD的度数为　　　　　,图③中,∠APD的度数为　　　　　; (3)根据前面的探索,你能否将本题推广到一般的正n边形的情况?若能,写出推广问题和结论;若不能,请说明理由.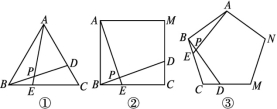    24.(12分)如图,已知△DCE的顶点C在∠AOB的平分线OP上,CD交OA于点F,CE交OB于点G.(1)如图①,若CD⊥OA,CE⊥OB,则图中有哪些相等的线段?请直接写出你的结论:　　　　　. (2)如图②,若∠AOB=120°,∠DCE=∠AOC,试判断线段CF与线段CG的数量关系,并加以证明.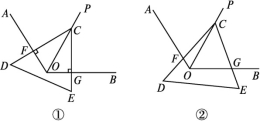
期中综合训练一、选择题1.D　2.B　3.D4.B　∵△ABC的角平分线AD、中线BE相交于点O,∴∠BAD=∠CAD,AE=CE,∴①③正确.5.C　全等三角形有3对,分别为Rt△ABO≌Rt△ADO,Rt△CDO≌Rt△CBO,△ADC≌△ABC.6.A　点(x,y)关于y轴对称的点是(-x,y),故b=20,a=13,则a+b=33.7.B8.B　∵AE=CF,∴AE+EF=CF+EF,即AF=CE.选项A,在△ADF和△CBE中,∵∴△ADF≌△CBE(ASA);选项B,根据AD=CB,AF=CE,∠AFD=∠CEB不能推出△ADF≌△CBE;选项C,在△ADF和△CBE中,∴△ADF≌△CBE(SAS);选项D,∵AD∥BC,∴∠A=∠C,易知△ADF≌△CBE(ASA).9.C　∵BD是AE的垂直平分线,∴AB=BE.∴∠E=∠A=52°,∴∠EBC=∠E+∠A=104°.10.B　如图,过点P作PM∥BC,交AC于点M.易知△APM是等边三角形.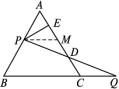∵PE⊥AM,∴AE=EM.∵PM∥CQ,∴∠PMD=∠QCD,∠MPD=∠Q.又PM=PA=CQ,∴△PMD≌△QCD.∴CD=DM,∴DE=ME+DM=(AM+MC)=AC=.二、填空题11.72°,72°,36°12.3　∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,∴CD=DE=1.在Rt△BDE中,∠C=90°,∠B=30°,∴BD=2DE=2,∴BC=CD+BD=1+2=3.13.11或13　由题意可得a-b-2=0,2a-3b-1=0,解得a=5,b=3,即三角形的三边长分别为5,5,3或3,3,5.所以此等腰三角形的周长为11或13.14.36　在△ACD中,∵AC=DC,∠D=15°,∴∠D=∠DAC=15°.∵∠ACB是△ACD的一个外角,∴∠ACB=∠D+∠DAC=15°+15°=30°.在Rt△ABC中,∠ACB=30°,∴AC=2AB=2×18=36(cm),即CD=36cm.15.315°　由题图可知∠4=×90°=45°,∠1和∠7所在的三角形全等,∴∠1+∠7=90°.同理,∠2+∠6=90°,∠3+∠5=90°,∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=3×90°+45°=315°.16.140°　如图,连接AD.∵点D在AB,AC的垂直平分线上,∴BD=AD,DC=AD,∴∠B=∠BAD,∠C=∠CAD.∵∠BAC=110°=∠BAD+∠CAD,∴∠B+∠C=110°.∴∠BDC=360°-(∠B+∠C)-∠BAC=360°-110°-110°=140°.三、解答题17.解(1)如图.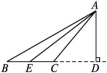(2)∠BAD=90°-30°=60°(直角三角形的两个锐角互余),∠ACD=180°-130°=50°(邻补角的定义),∠CAD=90°-50°=40°(直角三角形的两个锐角互余).18.解(1)如图.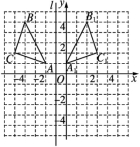(2)A1(0,1),B1(2,5),C1(3,2).19.解∵在△ABC中,AB=AC,∠BAC=120°,∴∠B=∠C=(180°-∠BAC)=(180°-120°)=30°.∵BD=BE,∴∠BED=∠BDE=(180°-∠B)=(180°-30°)=75°,∴∠ADE=90°-75°=15°.20.(1)解题图②中△ABE≌△ACD.证明如下:∵△ABC与△AED均为等腰直角三角形,∴AB=AC,AE=AD,∠BAC=∠EAD=90°.∴∠BAC+∠CAE=∠EAD+∠CAE,即∠BAE=∠CAD.∴△ABE≌△ACD.(2)证明由(1)知△ABE≌△ACD,∠ACD=∠ABE=45°.又∠ACB=45°,∴∠BCD=∠ACB+∠ACD=90°.∴DC⊥BE.21.解∵AD=DE,∴∠A=∠2.∵DE=BE,∴∠3=∠4.又∠2=∠3+∠4,∴∠4=∠2=∠A.∵BD=BC,∴∠1=∠C.又∠1=∠4+∠A=∠A+∠A=∠A,∴∠C=∠A.∵AB=AC,∴∠ABC=∠C=∠A.在△ABC中,∵∠A+∠ABC+∠C=180°,∴∠A+∠A+∠A=180°,即4∠A=180°,∴∠A=45°.22.证明如图,作DM⊥AB于点M,DN⊥AC于点N.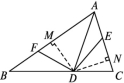∵△DBF和△DCE的面积相等,∴BF·DM=CE·DN.∵BF=CE,∴DM=DN.又DM⊥AB,DN⊥AC,∴AD平分∠BAC.23.解(1)60°　(2)90°　108°(3)能.如图,点E,D分别是正n边形ABCM…中以点C为顶点的相邻两边上的点,且BE=CD,BD与AE交于点P,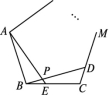则∠APD的度数为.24.解(1)CF=CG,OF=OG.(2)CF=CG.证明如下:如图,过点C作CM⊥OA于点M,CN⊥OB于点N,则∠CMF=∠CNG=90°.①又OC平分∠AOB,∴CM=CN, ②∠AOC=∠BOC.又∠AOB=120°,∴∠AOC=∠BOC=60°,∠MCN=360°-∠AOB-∠CMF-∠CNO=60°.∴∠DCE=∠AOC=60°.∴∠MCN=∠FCG.∴∠MCN-∠FCN=∠FCG-∠FCN,即∠1=∠2. ③由①②③得△CMF≌△CNG,∴CF=CG.