

山东省聊城市高唐县2022-2023学年八年级下学期期末数学试卷(含答案)
展开2022-2023学年山东省聊城市高唐县八年级(下)期末数学试卷
一、选择题(本大题共12个小题,每小题3分,共36分,在每小题列出的选项中,选出符合题目的一项)
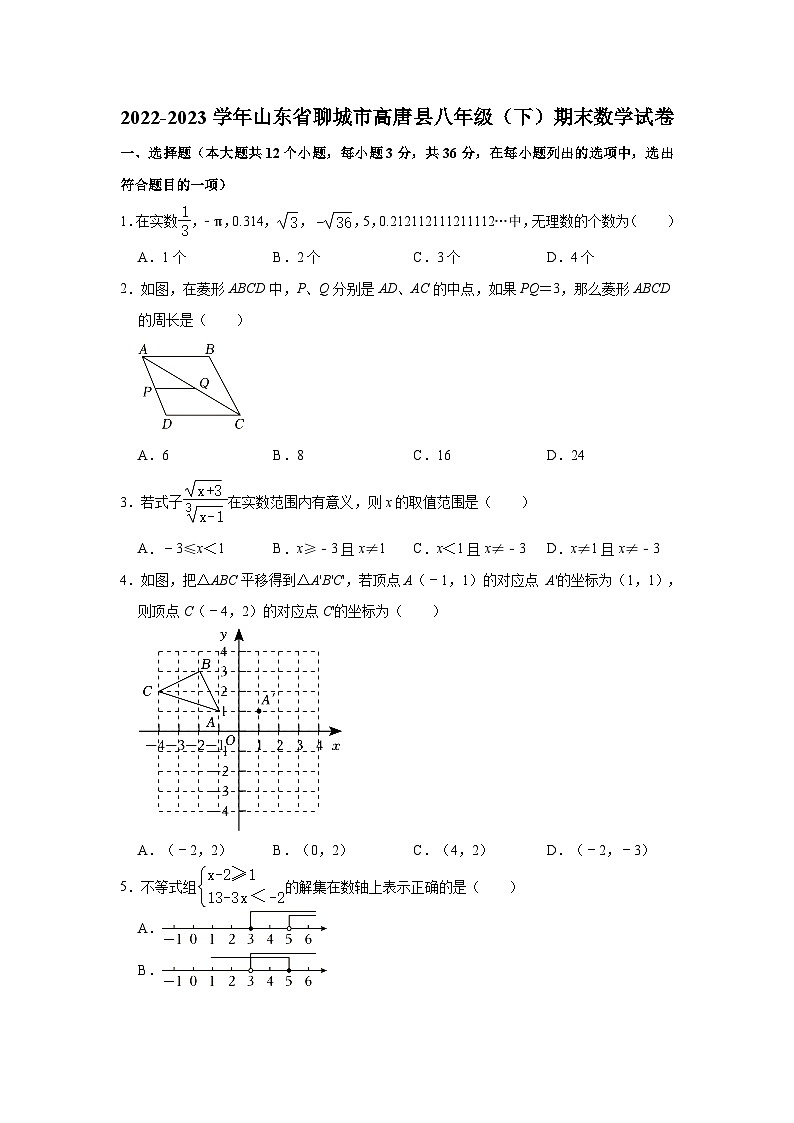
1.在实数,﹣π,0.314,,,5,0.212112111211112…中,无理数的个数为( )
A.1个 B.2个 C.3个 D.4个
2.如图,在菱形ABCD中,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的周长是( )
A.6 B.8 C.16 D.24
3.若式子在实数范围内有意义,则x的取值范围是( )
A.﹣3≤x<1 B.x≥﹣3且x≠1 C.x<1且x≠﹣3 D.x≠1且x≠﹣3
4.如图,把△ABC平移得到△A'B'C',若顶点A(﹣1,1)的对应点 A'的坐标为(1,1),则顶点C(﹣4,2)的对应点C'的坐标为( )
A.(﹣2,2) B.(0,2) C.(4,2) D.(﹣2,﹣3)
5.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
6.如图,线段DE与AF分别为△ABC的中位线与中线.在下列条件中,不能够判定四边形ADFE为菱形的是( )
A.AB=AC B.AF⊥BC C.∠BAF=∠CAF D.BC=2AF
7.已知A(x1,y1)B(x2,y2) 为直线y=2x﹣3上不相同的两个点,以下判断正确的是( )
A.(x1﹣x2)(y1﹣y2)>0 B.(x1﹣x2)(y1﹣y2)<0
C.(x1﹣x2)(y1﹣y2)≥0 D.(x1﹣x2)(y1﹣y2)≤0
8.如图,正方形ABCD的边长为4cm,点F为对角线AC上一点,当∠CBF=22.5°时,则CF的长是( )
A.4cm B. C.2cm D.
9.已知关于x的不等式组的解集中有且仅有3个整数,则a的取值范围是( )
A.5<a≤6 B.5<a<6 C.5≤a<6 D.5≤a≤6
10.如图,点A(﹣2,6),B(﹣4,2),当直线y=kx﹣2(k≠0)与线段AB有交点时,k的取值范围是( )
A.k≤﹣1 B.k≥﹣4 C.k≤﹣4或k≥﹣1 D.﹣4≤k≤﹣1
11.如图,在Rt△ABC中,∠ACB=90°,∠B=65°,以点C为中心,将△ABC 顺时针旋转90°,得到△DEC,点B的对应点E落在AC上,连接AD,则∠ADE的度数为( )
A.45° B.30° C.20° D.15°
12.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:
①方程组的解为;
②直线l1:y=kx+b的k=2;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题(本大题共5个小题,满分15分,只要求填写最后结果,每小题填对得3分)
13.不等式组的解集是 .
14.一个正数x的两个平方根分别是a+2和a﹣4,则a= .
15.如图,直线y1=k1x与直线y2=k2x+b交于点A(1,2).当y1>y2时,x的取值范围是 .
16.如图,矩形ABCD中,AB=6,AD=10.在边AD上取一点E,使 BE=BC,过点C作CF⊥BE,垂足为点F,则BF的长为 .
17.如图,直线l的函数表达式为y=x﹣1,在直线l上顺次取点A1(2,1),A2(3,2),A3(4,3),A4(5,4)…,若这些点构成形如“┐”的图形的阴影部分面积分别表示为S1,S2,S3,…Sn,则S2023= .
三、解答题(本大题共8个小题,共69分解答应写出文字说明,证明过程或演算步
18.计算:
(1);
(2).
19.解不等式(组):
(1)解不等式 ;
(2)解不等式组,并把解集在数轴上表示出来.
20.如图,△ABC的顶点坐标为A(﹣2,3),B(﹣3,1),C(﹣1,2).
(1)画出△ABC向右平移3个单位后的△A1B1C1;
(2)将△ABC绕原点O旋转180°,画出旋转后的△A2B2C2;
(3)△A2B1C1的面积为 .
21.图1是某品牌婴儿车,图2为其简化结构示意图.根据安全标准需满足BC⊥CD,现测得AB=CD=6dm,BC=3dm,AD=9dm,其中AB与BD之间由一个固定为90°的零件连接(即∠ABD=90°),通过计算说明该车是否符合安全标准.
22.如图,在▱ABCD中,点O是对角线AC的中点.某数学学习小组要在AC上找两点E,F,使四边形BEDF为平行四边形,现总结出甲、乙两种方案如下:
甲方案
乙方案
分别取AO,CO的中点E,F
作BE⊥AC于点E,DF⊥AC于点F
请回答下列问题:
(1)以上方案能得到四边形BEDF为平行四边形的是 ,选择其中一种并证明,若不能,请说明理由;
(2)若EF=2AE,S△AED=6,求▱ABCD的面积.
23.用充电器给某手机充电时,其屏幕的起始画面如图1.
经测试,在用快速充电器和普通充电器对该手机充电时,其电量E(单位:%)与充电时间t(单位:h)的函数图象分别为图2中的线段AB、AC.
(1)求线段AC对应的函数表达式;
(2)已知该手机正常使用时耗电量为10%/h,在用快速充电器将其充满电后,正常使用ah,接着再用普通充电器将其充满电,其“充电一耗电一充电”的时间恰好是6h,求a的值.
24.在我校“数学项目化学习”中,学生使用甲、乙两种原料配制奶茶.两种原料的蛋白质含量及价格如表:
原料
甲
乙
蛋白质的含量/(单位/kg)
600
100
原料价格/(元/kg)
8
4
(1)现配制这种奶茶10kg,要求至少含有4200单位的蛋白质,求出所需甲种原料的质量x(kg)的取值范围.
(2)如果仅要求购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量x(kg)的取值范围.
25.问题情境:四边形ABCD中,点O是对角线AC的中点,点E是直线AC上的一个动点(点E与点C、O、A都不重合)过点A,C分别作直线BE的垂线,垂足分别为F、G,连接OF,OG.
(1)初步探究:已知四边形ABCD是正方形,且点E在线段OC上,求证AF=BG;
(2)探究图中OF与OG的数量关系,并说明理由.
参考答案
一、选择题(本大题共12个小题,每小题3分,共36分,在每小题列出的选项中,选出符合题目的一项)
1.在实数,﹣π,0.314,,,5,0.212112111211112…中,无理数的个数为( )
A.1个 B.2个 C.3个 D.4个
【分析】整数和分数统称为有理数,无理数即无限不循环小数,据此进行判断即可.
解:=﹣6,
所以在实数,﹣π,0.314,,,5,0.212112111211112…中,无理数有﹣π,,0.212112111211112…,共3个.
故选:C.
【点评】本题考查无理数的识别和算术平方根,熟练掌握相关概念是解题的关键.
2.如图,在菱形ABCD中,P、Q分别是AD、AC的中点,如果PQ=3,那么菱形ABCD的周长是( )
A.6 B.8 C.16 D.24
【分析】根据三角形的中位线定理,即可求得CD的长,进而求得菱形的周长.
解:∵P、Q分别是AD、AC的中点,
∴PQ是△ADC的中位线,
∴PQ=3,
∴CD=2PQ=6,
∴菱形ABCD的周长是6×4=24.
故选:D.
【点评】本题主要考查了菱形的性质,以及三角形的中位线定理,正确求得CD的长是关键.
3.若式子在实数范围内有意义,则x的取值范围是( )
A.﹣3≤x<1 B.x≥﹣3且x≠1 C.x<1且x≠﹣3 D.x≠1且x≠﹣3
【分析】根据二次根式和分式有意义的条件列不等式组求解.
解:由题意可得,
解得x≥﹣3且x≠1.
故选:B.
【点评】本题考查二次根式和分式有意义的条件,理解二次根式有意义的条件(被开方数为非负数),分式有意义的条件(分母不能为零)是解题关键.
4.如图,把△ABC平移得到△A'B'C',若顶点A(﹣1,1)的对应点 A'的坐标为(1,1),则顶点C(﹣4,2)的对应点C'的坐标为( )
A.(﹣2,2) B.(0,2) C.(4,2) D.(﹣2,﹣3)
【分析】根据平移坐标的变化规律进行计算即可.
解:由于把△ABC平移得到△A'B'C',顶点A(﹣1,1)的对应点 A'的坐标为(1,1)可知,平移的方向是沿着x正方向,平移2个单位,
所以顶点C(﹣4,2)的对应点C'的坐标(﹣2,2),
故选:A.
【点评】本题考查平移坐标变化,掌握平移坐标的变化规律是正确解答的关键.
5.不等式组的解集在数轴上表示正确的是( )
A.
B.
C.
D.
【分析】先解出每个不等式的解集,即可得到不等式组的解集,然后在数轴上表示出其解集即可.
解:,
解不等式①,得:x≥3,
解不等式②,得:x>5,
∴该不等式组的解集是x>5,
其解集在数轴上表示如下:
,
故选:A.
【点评】本题考查解一元一次不等式组、在数轴上表示不等式的解集,解答本题的关键是明确解一元一次不等式的方法.
6.如图,线段DE与AF分别为△ABC的中位线与中线.在下列条件中,不能够判定四边形ADFE为菱形的是( )
A.AB=AC B.AF⊥BC C.∠BAF=∠CAF D.BC=2AF
【分析】菱形的判定:一组邻边相等的平行四边形是菱形;四条边都相等的四边形是菱形;对角线互相垂直的平行四边形是菱形,由此即可判断.
解:∵DE与AF分别为△ABC的中位线与中线,
∴D、F、E分别是AB、BC、AC的中点,
∴DF,EF是△ABC的中位线,
∴DF∥AC,FE∥AB,
∴四边形ADFE是平行四边形,
A、AB=AC,由D、E分别是AB、AC的中点,得到AD=AE,因此四边形ADFE是菱形,故A不符合题意;
B、AF⊥BC,由DE是△ABC的中位线,得到DE∥BC,推出AF⊥DE,因此四边形ADFE是菱形,故B不符合题意;
C、∠BAF=∠CAF,由AD∥EF,得到∠BAF=∠AFE,推出∠CAF=∠AFE,得到AE=FE,因此四边形ADFE是菱形,故C不符合题意;
D、BC=2AF,得不到四边形ADFE是菱形,故D符合题意.
故选:D.
【点评】本题考查菱形的判定,三角形中位线定理,关键是掌握菱形的判定方法.
7.已知A(x1,y1)B(x2,y2) 为直线y=2x﹣3上不相同的两个点,以下判断正确的是( )
A.(x1﹣x2)(y1﹣y2)>0 B.(x1﹣x2)(y1﹣y2)<0
C.(x1﹣x2)(y1﹣y2)≥0 D.(x1﹣x2)(y1﹣y2)≤0
【分析】将两个点代入直线方程整理判断即可.
解:将A、B两点坐标分别代入直线方程,得y1=2x1+3,y2=﹣2x2+3,则y1﹣y2=﹣2(x1﹣x2).
(x1﹣x2)(y1﹣y2)=2(x1﹣x2)2≥0.
∵A、B两点不相同,
∴x1﹣x2≠0,
∴(x1﹣x2)(y1﹣y2)>0.
故选:A.
【点评】本题主要考查一次函数图象上点的坐标,比较简单,分别代入计算整理即可.
8.如图,正方形ABCD的边长为4cm,点F为对角线AC上一点,当∠CBF=22.5°时,则CF的长是( )
A.4cm B. C.2cm D.
【分析】根据正方形的性质得出∠ABC=90°,∠ACD=∠ACB=×90°=45°,求出∠ABF=90°﹣22.5°=67.5°,∠AFB=∠BCF+∠CBF=67.5°,得出∠ABF=∠AFB,根据等腰三角形的判定求出AF,再根据勾股定理求出AC,即可得出答案.
解:∵四边形ABCD为正方形,
∴∠ABC=90°,∠ACD=∠ACB=×90°=45°,
∵∠CBF=22.5°,
∴∠ABF=90°﹣22.5°=67.5°,
∠AFB=∠BCF+∠CBF=67.5°,
∴∠ABF=∠AFB,
∴AF=AB=4cm.
∵AC=cm,
∴CF=AC﹣AF=cm.
故选:B.
【点评】本题主要考查了正方形的性质,三角形外角的性质,等腰三角形的判定,勾股定理,解题的关键是熟练掌握正方形的性质,得出∠ABF=∠AFB.
9.已知关于x的不等式组的解集中有且仅有3个整数,则a的取值范围是( )
A.5<a≤6 B.5<a<6 C.5≤a<6 D.5≤a≤6
【分析】先根据不等式的性质求出不等式的解集,再根据求不等式组解集的规律求出不等式组的解集,再根据不等式组的整数解得出答案即可.
解:,
解不等式①,得x<a,
解不等式②,得x>2,
所以不等式组的解集是2<x<a,
∵关于x的不等式组的解集中有且仅有3个整数(是3,4,5),
∴5<a≤6,
故选:A.
【点评】本题考查了解一元一次不等式组和一元一次不等式组的整数解,能根据求不等式组解集的规律求出不等式组的解集是解此题的关键.
10.如图,点A(﹣2,6),B(﹣4,2),当直线y=kx﹣2(k≠0)与线段AB有交点时,k的取值范围是( )
A.k≤﹣1 B.k≥﹣4 C.k≤﹣4或k≥﹣1 D.﹣4≤k≤﹣1
【分析】分别求得直线y=kx﹣2的图象点A、B时相应的k的值,再根据与线段AB有交点,确定k的取值范围.
解:将A(﹣2,6)代入y=kx﹣2中得:6=﹣2k﹣2,
解得k=﹣4,
将B(﹣4,2)代入y=kx﹣2中得:2=﹣4k﹣2,
解得k=﹣1,
∴当直线y=kx﹣2与线段AB有交点时,k的取值范围为:﹣4≤k≤﹣1,
故选:D.
【点评】本题主要考查了一次函数图象与系数的关系,一次函数图象上点的坐标的特征,利用待定系数法求出临界值是解题的关键.
11.如图,在Rt△ABC中,∠ACB=90°,∠B=65°,以点C为中心,将△ABC 顺时针旋转90°,得到△DEC,点B的对应点E落在AC上,连接AD,则∠ADE的度数为( )
A.45° B.30° C.20° D.15°
【分析】先根据旋转的性质得到∴∠ACD=90°,CA=CD,∠DEC=∠B=65°,则可判断△ACD为等腰直角三角形,所以∠DAC=45°,然后根据三角形外角性质计算出∠ADE的度数.
解:∵△ABC顺时针旋转90°得到△DEC,
∴∠ACD=90°,CA=CD,∠DEC=∠B=65°,
∴△ACD为等腰直角三角形,
∴∠DAC=45°,
∵∠DEC=∠DAE+∠ADE,
∴∠ADE=65°﹣45°=20°.
故选:C.
【点评】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.
12.已知直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),直线l1交y轴于点B(0,4),交x轴于点A,直线l2交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:
①方程组的解为;
②直线l1:y=kx+b的k=2;
③S△ABD=6;
④当PA+PC的值最小时,点P的坐标为(0,1).
其中正确的说法是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【分析】①根据一次函数图象与二元一次方程的关系,利用交点坐标可得方程组的解;
②利用待定系数法求得k的值;
③求得BD和AO的长,根据三角形面积计算公式,即可得到△ABD的面积;
④根据轴对称的性质以及两点之间,线段最短,即可得到当PA+PC的值最小时,点P的坐标为(0,1).
解:①∵直线l1:y=kx+b与直线l2:y=﹣x+m都经过C(﹣,),
∴方程组的解为,
故①正确,符合题意;
②把B(0,4),C(﹣,)代入直线l1:y=kx+b,可得,
解得,
∴故②正确,符合题意;
③把C(﹣,)代入直线l2:y=﹣x+m,可得m=1,
y=﹣x+1中,令x=0,则y=1,
∴D(0,1),
∴BD=4﹣1=3,
在直线l1:y=2x+4中,令y=0,则x=﹣2,
∴A(﹣2,0),
∴AO=2,
∴S△ABD=×3×2=3,
故③错误,不符合题意;
④点A关于y轴对称的点为A'(2,0),
由点C、A′的坐标得,直线CA′的表达式为:y=﹣x+1,
令x=0,则y=1,
∴当PA+PC的值最小时,点P的坐标为(0,1),
故④正确,符合题意;
故选:B.
【点评】本题为一次函数综合题,主要考查了一次函数图象与性质,三角形面积以及最短距离问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.
二、填空题(本大题共5个小题,满分15分,只要求填写最后结果,每小题填对得3分)
13.不等式组的解集是 x≥4 .
【分析】按照解一元一次不等式组的步骤,进行计算即可解答.
解:,
解不等式①得:x≥4,
解不等式②得:x>﹣2,
∴原不等式组的解集为:x≥4,
故答案为:x≥4.
【点评】本题考查了解一元一次不等式组,熟练掌握解一元一次不等式组的步骤是解题的关键.
14.一个正数x的两个平方根分别是a+2和a﹣4,则a= 1 .
【分析】根据一个正数的平方根有2个,且互为相反数列出方程,求出方程的解得到a的值,即可确定出x的值.
解:根据题意得:a+2+a﹣4=0,
解得:a=1.
故答案为:1.
【点评】此题考查了平方根,熟练掌握平方根的定义是解本题的关键.
15.如图,直线y1=k1x与直线y2=k2x+b交于点A(1,2).当y1>y2时,x的取值范围是 x>1 .
【分析】根据两函数的交点坐标和函数的图象得出x的范围即可.
解:∵直线y1=k1x与直线y2=k2x+b交于点A(1,2),
∴当y1>y2时,x的取值范围是x>1,
故答案为:x>1.
【点评】本题考查了一次函数与一元一次不等式,能正确根据函数图象得出不等式的解集是解此题的关键.
16.如图,矩形ABCD中,AB=6,AD=10.在边AD上取一点E,使 BE=BC,过点C作CF⊥BE,垂足为点F,则BF的长为 8 .
【分析】根据矩形的性质可得出∠AEB=∠FBC,结合已知BE=BC,利用AAS证得△ABE和△FCB全等,得出FC=AB=6,再根据矩形的性质得到BC=AD=10,从而在Rt△FCB中利用勾股定理求出BF的长.
解:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠AEB=∠FBC,
∵CF⊥BE,
∴∠CFB=90°,
∴∠CFB=∠A,
在△ABE和△FCB中,
,
∴△ABE≌△FCB(AAS),
∴FC=AB=6,
∵四边形ABCD是矩形,
∴BC=AD=10,
在Rt△FCB中,由勾股定理得,
故答案为:8.
【点评】本题考查了矩形的性质,三角形全等的性质与判定,勾股定理,熟知矩形的对边平行且相等,四个角都是直角.
17.如图,直线l的函数表达式为y=x﹣1,在直线l上顺次取点A1(2,1),A2(3,2),A3(4,3),A4(5,4)…,若这些点构成形如“┐”的图形的阴影部分面积分别表示为S1,S2,S3,…Sn,则S2023= 4048 .
【分析】根据图形分别求出S1,S2,S3的值,得出规律,根据规律即可求解.
解:由题意得,
S1=2×3﹣2×1=4=2×(1+1),
S2=4×3﹣3×2=6=2×(2+1),
S3=5×4﹣4×3=8=2×(3+1),
...,
∴Sn=2(n+1),
∴S2023=2×(2023+1)=4048,
故答案为:4048.
【点评】本题考查了一次函数图象上点的坐标特征,矩形的面积,以及规律型,根据点的坐标的变化找出阴影部分面积的变化规律是解题的关键.
三、解答题(本大题共8个小题,共69分解答应写出文字说明,证明过程或演算步
18.计算:
(1);
(2).
【分析】(1)先算括号里的运算,再算乘法,最后算减法即可;
(2)先化简,再算加减即可.
解:(1)
=(2)×
=3
=9
=4;
(2)
=(6)+3
=
=.
【点评】本题主要考查二次根式的混合运算,解答的关键是对相应的运算法则的掌握.
19.解不等式(组):
(1)解不等式 ;
(2)解不等式组,并把解集在数轴上表示出来.
【分析】(1)按照解一元一次不等式的步骤,进行计算即可解答;
(2)按照解一元一次不等式组的步骤,进行计算即可解答.
解:(1),
2(x﹣3)<3(2x+1)﹣6,
2x﹣6<6x+3﹣6,
2x﹣6x<3﹣6+6,
﹣4x<3,
x>﹣;
(2),
解不等式①得:x≥﹣1,
解不等式②得:x≤2,
∴原不等式组的解集为:﹣1≤x≤2,
∴该不等式组的解集在数轴上表示如图所示:
【点评】本题考查了解一元一次不等式组,解一元一次不等式,在数轴上表示不等式的解集,准确熟练地进行计算是解题的关键.
20.如图,△ABC的顶点坐标为A(﹣2,3),B(﹣3,1),C(﹣1,2).
(1)画出△ABC向右平移3个单位后的△A1B1C1;
(2)将△ABC绕原点O旋转180°,画出旋转后的△A2B2C2;
(3)△A2B1C1的面积为 5 .
【分析】(1)根据平移的性质找到A,B,C向右平移3个单位的对应点A1,B1,C1,顺次连接,得到△A1B1C1;
(2)根据中心对称的性质,找到A,B,C关于原点对称的点A2,B2,C2,顺次连接,得到△A2B2C2;
(3)连接A2B1,A2C1,根据网格的特点以及三角形面积公式即可求解.
解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
(3)如图所示,连接A2B1,A2C1,
则A2C1=5,B1到A2C1的距离为2,
∴△A2B1C1的面积为,
故答案为:5.
【点评】本题考查了平移作图,画中心对称图形,坐标与图形,熟练掌握平移的性质以及中心对称的性质是解题的关键.
21.图1是某品牌婴儿车,图2为其简化结构示意图.根据安全标准需满足BC⊥CD,现测得AB=CD=6dm,BC=3dm,AD=9dm,其中AB与BD之间由一个固定为90°的零件连接(即∠ABD=90°),通过计算说明该车是否符合安全标准.
【分析】在Rt△ABD中,由勾股定理求出BD,在△BCD中,通过计算,根据勾股定理逆定理判断即可.
解:在Rt△ABD中,BD2=AD2﹣AB2=92﹣62=45,
在△BCD中,BC2+CD2=32+62=45,
∴BC2+CD2=BD2,
∴∠BCD=90°,
∴BC⊥CD.
故该车符合安全标准.
【点评】本题主要考查了勾股定理和勾股定理逆定理,熟练掌握勾股定理逆定理的应用是解决问题的关键.
22.如图,在▱ABCD中,点O是对角线AC的中点.某数学学习小组要在AC上找两点E,F,使四边形BEDF为平行四边形,现总结出甲、乙两种方案如下:
甲方案
乙方案
分别取AO,CO的中点E,F
作BE⊥AC于点E,DF⊥AC于点F
请回答下列问题:
(1)以上方案能得到四边形BEDF为平行四边形的是 甲方案或乙方案 ,选择其中一种并证明,若不能,请说明理由;
(2)若EF=2AE,S△AED=6,求▱ABCD的面积.
【分析】(1)甲方案,由平行四边形的性质得AB∥CD,AB=CD,则∠BAE=∠DCF,由AO=CO,E、F分别是AO、CO的中点,得AE=CF,可证明△ABE≌△CDF,得BE=DF,∠AEB=∠CFD,所以∠BEF=∠DFE,则BE∥DF,即可证明四边形BEDF是平行四边形;
乙方案,由BE⊥AC于点E,DF⊥AC于点F,得BE∥DF,∠AEB=∠CFD=90°,由平行四边形的性质得AB∥CD,AB=CD,则∠BAE=∠DCF,可证明△ABE≌△CDF,得BE=DF,即可证明四边形BEDF是平行四边形;
(2)由AO=CO,AE=CF,推导出OE=OF,则EF=2AE=2OE,所以OE=AE=CF=OF,则S△ABC=S△ADC=4S△AED=24,所以S▱ABCD=48.
解:(1)甲方案,证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
∵O是对角线AC的中点,
∴AO=CO,
∵E、F分别是AO、CO的中点,
∴AE=AO,CF=CO,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF,∠AEB=∠CFD,
∵∠BEF=180°﹣∠AEB,∠DFE=180°﹣∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四边形BEDF是平行四边形.
乙方案,证明:∵BE⊥AC于点E,DF⊥AC于点F,
∴BE∥DF,∠AEB=∠CFD=90°,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∴四边形BEDF是平行四边形.
(2)解:由(1)得△ABE≌△CDF,
∴AE=CF,
∴AO﹣AE=CO﹣CF,
∴OE=OF,
∴EF=2OE,
∵EF=2AE,
∴2OE=2AE,
∴OE=AE=CF=OF,
∴S△ABC=S△ADC=4S△AED=4×6=24,
∴S▱ABCD=2×24=48,
∴▱ABCD的面积是48.
【点评】此题重点考查平行四边形的判定与性质、全等三角形的判定与性质等知识,证明△ABE≌△CDF是解题的关键.
23.用充电器给某手机充电时,其屏幕的起始画面如图1.
经测试,在用快速充电器和普通充电器对该手机充电时,其电量E(单位:%)与充电时间t(单位:h)的函数图象分别为图2中的线段AB、AC.
(1)求线段AC对应的函数表达式;
(2)已知该手机正常使用时耗电量为10%/h,在用快速充电器将其充满电后,正常使用ah,接着再用普通充电器将其充满电,其“充电一耗电一充电”的时间恰好是6h,求a的值.
【分析】(1)设线段AC的函数表达式为E=kt+b,利用待定系数法求解即可;
(2)根据题意列出方程,然后解方程求解即可.
解:(1)设线段AC的函数表达式为E=kt+b(0<t≤6),
将(0,20),(6,100)代入E=kt+b,
即,
解得,
∴线段AC的函数表达式为(0<t≤6);
(2)根据题意,得,
∴.
【点评】本题考查的一次函数的实际应用,同时考查一元一次方程的应用,掌握以上知识是解题的关键.
24.在我校“数学项目化学习”中,学生使用甲、乙两种原料配制奶茶.两种原料的蛋白质含量及价格如表:
原料
甲
乙
蛋白质的含量/(单位/kg)
600
100
原料价格/(元/kg)
8
4
(1)现配制这种奶茶10kg,要求至少含有4200单位的蛋白质,求出所需甲种原料的质量x(kg)的取值范围.
(2)如果仅要求购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量x(kg)的取值范围.
【分析】(1)设需要甲种原料xkg,则需要乙种原料(10﹣x)kg,然后根据要求至少含有4200单位的蛋白质列出不等式求解即可;
(2)根据购买甲、乙两种原料的费用不超过72元结合(1)所求,建立关于x的不等式组进行求解即可.
解:(1)设需要甲种原料xkg,则需要乙种原料(10﹣x)kg,
由题意得600x+100(10﹣x)≥4200,
∴600x+1000﹣100x≥4200,
解得x≥6.4;
∴所需甲种原料的质量x(kg)的取值范围为x≥6.4.
(2)由题意得,
解得6.4≤x≤8.
∴所需甲种原料的质量x(kg)的取值范围为6.4≤x≤8.
【点评】本题主要考查了一元一次不等式的实际应用,一元一次不等式组的实际应用,正确理解题意找到不等关系是解题的关键.
25.问题情境:四边形ABCD中,点O是对角线AC的中点,点E是直线AC上的一个动点(点E与点C、O、A都不重合)过点A,C分别作直线BE的垂线,垂足分别为F、G,连接OF,OG.
(1)初步探究:已知四边形ABCD是正方形,且点E在线段OC上,求证AF=BG;
(2)探究图中OF与OG的数量关系,并说明理由.
【分析】(1)根据正方形的性质证明△ABF≌△BCG(AAS)即可得出结论;
(2)延长GO交AF于H,证明△AOH≌△COG(ASA),得OH=OG,再根据直角三角形斜边上的中线等于斜边的一半得出结论.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵AF⊥BE,CG⊥BE,
∴∠AFB=∠BGC=90°,
∴∠BAF=90°﹣∠ABF=∠CBG,
在△ABF和△BCG中,
,
∴△ABF≌△BCG(AAS),
∴AF=BG;
(2)解:OF=OG,理由如下:
如图,延长GO交AF于H,
∵AF⊥BE,CG⊥BE,
∴AF∥CG,
∴∠FAO=∠OCG,
∵AO=OC,∠AOH=∠COG,
在△AOH和△COG中,
∴△AOH≌△COG(ASA),
∴OH=OG,
在Rt△HFG中,FO=HG=OG.
∴OF=OG.
【点评】本题考查了正方形的性质、全等三角形的性质和判定,直角三角形的性质,解决本题的关键是得到△AOH≌△COG.
山东省聊城市高唐县第一实验中学2023-2024学年八年级上学期期末数学试卷: 这是一份山东省聊城市高唐县第一实验中学2023-2024学年八年级上学期期末数学试卷,共6页。
2023-2024学年山东省聊城市高唐县八年级(上)期中数学试卷(含解析): 这是一份2023-2024学年山东省聊城市高唐县八年级(上)期中数学试卷(含解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省聊城市高唐县八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年山东省聊城市高唐县八年级(下)期末数学试卷(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












