第5章相交线平行线单元小结 (3)课件PPT

这是一份第5章相交线平行线单元小结 (3)课件PPT，共35页。

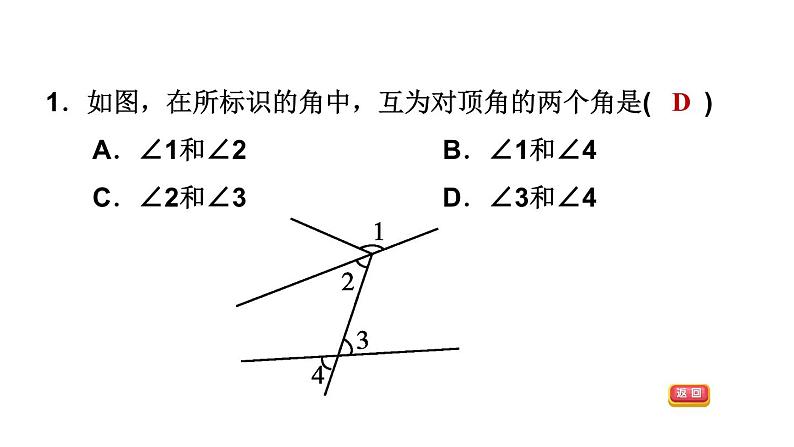
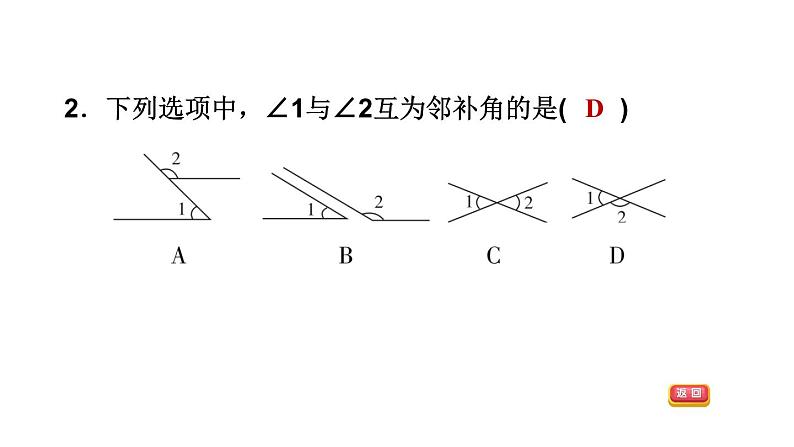
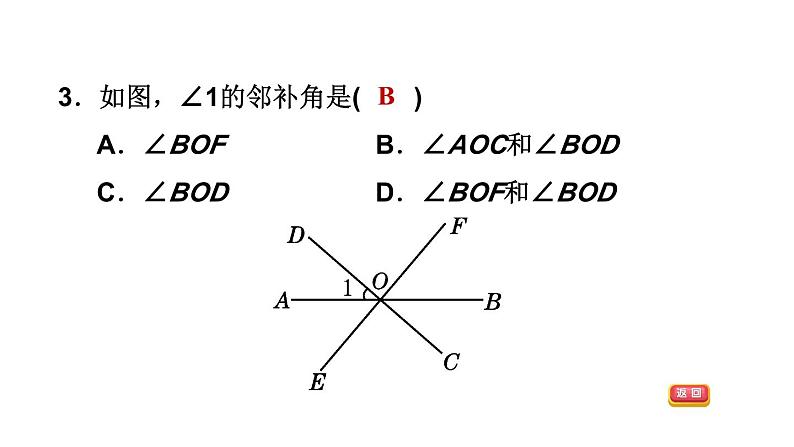
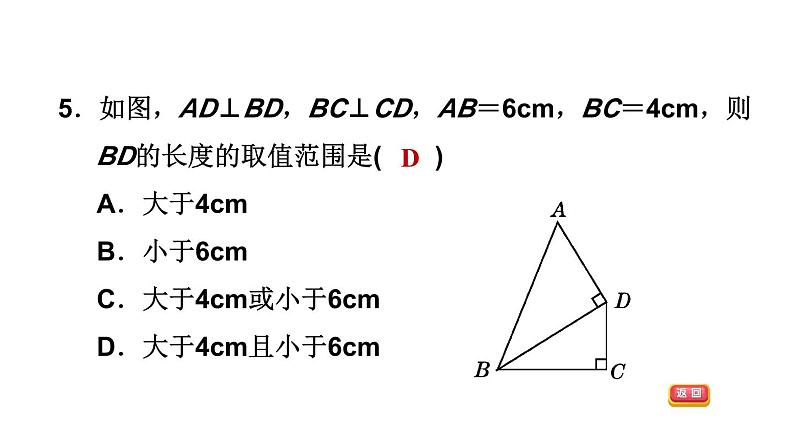
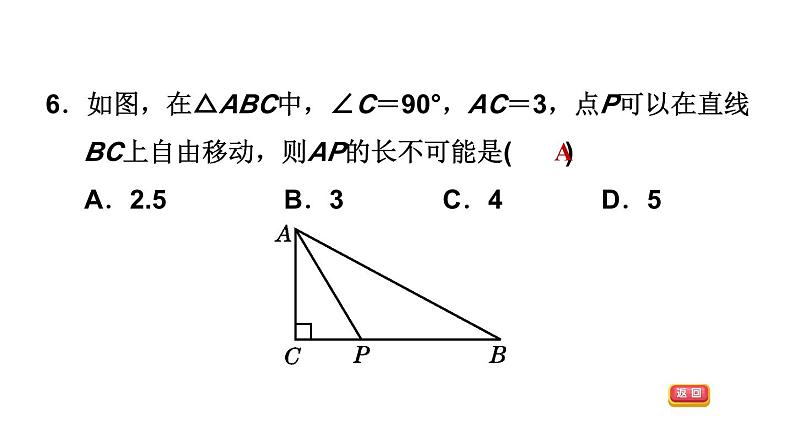
全章整合与提升第5章　相交线与平行线答案显示AD见习题见习题DDDBBD见习题见习题DB75°见习题见习题见习题见习题1．如图，在所标识的角中，互为对顶角的两个角是(　　)A．∠1和∠2 B．∠1和∠4C．∠2和∠3 D．∠3和∠4D2．下列选项中，∠1与∠2互为邻补角的是(　　)D3．如图，∠1的邻补角是(　　)A．∠BOF B．∠AOC和∠BODC．∠BOD D．∠BOF和∠BODB4．下列说法正确的有(　　)①在平面内，过直线上一点有且只有一条直线垂直于已知直线；②在平面内，过直线外一点有且只有一条直线垂直于已知直线；③在平面内，过一点有无数条直线垂直于已知直线；④在平面内，有且只有一条直线垂直于已知直线．A．1个 B．2个 C．3个 D．4个B5．如图，AD⊥BD，BC⊥CD，AB＝6cm，BC＝4cm，则BD的长度的取值范围是(　　)A．大于4cmB．小于6cmC．大于4cm或小于6cmD．大于4cm且小于6cmD6．如图，在△ABC中，∠C＝90°，AC＝3，点P可以在直线BC上自由移动，则AP的长不可能是(　　)A．2.5 B．3 C．4 D．5A7．[中考·金华]如图，∠B的同位角可以是(　　)A．∠1 B．∠2 C．∠3 D．∠4D8．如图，直线AB，BD交于点B，直线EF，BD，AC交于点C，则：(1)∠1和∠ABC是直线AB，EF被直线________所截得的________角；(2)∠2和∠BAC是直线EF，AB被直线________所截得的________角；BD同位AC内错(3)∠3和∠ABC是直线________，________被直线________所截得的________角；(4)∠ABC和∠ACD是直线________，________被直线________所截得的________角；(5)∠ABC和∠BCE是直线________，________被直线________所截得的________角．ABACCB同旁内ABACDB同位ABEFBD同旁内9．如图，直线AB，CD被直线EF所截，交AB，CD于点M，N，NH是一条射线，图中共有多少对同位角？多少对内错角？多少对同旁内角？分别列出这些角．解：同位角：∠EMA和∠MNC，∠EMB和∠END，∠AMN和∠CNF，∠BMN和∠DNF，∠EMB和∠MNH，∠BMN和∠HNF，共6对；同旁内角：∠AMN和∠MNC，∠BMN和∠MND，∠BMN和∠MNH，共3对；内错角：∠AMN和∠MNH，∠AMN和∠MND，∠BMN和∠MNC，共3对．10．如图，直线AB、CD相交于点O，OE⊥AB于点O，OF平分∠AOE，∠1＝15°30′，则下列结论中不正确的是(　　)A．∠AOD与∠1互为补角B．∠1的余角74°30′C．∠2＝45°D．∠DOF＝135°【点拨】∠DOF＝180°－45°－15°30′＝119°30′，故选D.【答案】D11.如图，两直线AB、CD相交于点O，OE平分∠BOD，∠AOC∶∠AOD＝7∶11.(1)求∠COE的度数；(2)若OF⊥OE，求∠COF的度数．解：∵OF⊥OE，∴∠FOE＝90°.又∵∠DOE＝35°，∴∠FOD＝90°－∠DOE＝90°－35°＝55°.　∴∠COF＝180°－∠FOD＝180°－55°＝125°.12．如图，由点O引出六条射线OA、OB、OC、OD、OE、OF，且AO⊥OB，OF平分∠BOC，OE平分∠AOD.若∠EOF＝170°，求∠COD的度数．【点拨】有些复杂的求角度的问题用方程思想求解非常简单，注意方程思想的应用．13．如果两个角的两边分别平行，而其中一个角比另一个角的3倍少20°，那么这两个角的度数是(　　)A．50°和130° B．60°和160°C．10°和10° D．以上都不对【点拨】首先由两个角的两边分别平行，可得这两个角相等或互补．然后设其中一角为x°，由其中一个角比另一个角的3倍少20°，分别从两个角相等与互补去分析，即可求得这两个角为50°和130°或10°和10°，注意别漏解．【答案】D14．如图，若AB∥CD，∠ABE和∠CDE的平分线交于点F，且∠BED＝105°，那么∠BFD等于(　　)A．60° B．52.5° C．53.5° D．41°B15．[中考·衡阳]将一副三角尺如图放置，使点A落在DE上，若BC∥DE，则∠AFC的度数为________．【点拨】∵BC∥DE，∴∠BCE＝∠E＝30°.∵∠ACB＝90°－45°＝45°，∴∠ACF＝∠ACB－∠BCE＝45°－30°＝15°，∴∠AFC＝180°－90°－∠ACF＝180°－90°－15°＝75°.【答案】75°16．如图，已知∠BEF＝70°，∠B＝70°，∠DCE＝140°，且CD∥AB.求∠CEF的度数．解：∵∠BEF＝70°，∠B＝70°，∴∠BEF＝∠B.∴AB∥EF.又∵CD∥AB，∴EF∥CD.∴∠DCE＋∠CEF＝180°.又∵∠DCE＝140°，∴∠CEF＝180°－140°＝40°.17．[中考·益阳]如图，AB∥CD，∠1＝∠2.试说明：AM∥CN.解：∵AB∥CD，∴∠EAB＝∠ECD.∵∠1＝∠2，∴∠EAM＝∠ECN，∴AM∥CN.18．如图，∠ADE＋∠BCF＝180°，BE平分∠ABC，∠ABC＝2∠E.(1)AD与BC平行吗？请说明理由；解：AD∥BC.理由如下：∵∠ADE＋∠ADF＝180°，∠ADE＋∠BCF＝180°，∴∠ADF＝∠BCF，∴AD∥BC.(2)AB与EF存在怎样的位置关系？为什么？解：AB∥EF.理由如下：∵BE平分∠ABC，∴∠ABC＝2∠ABE.又∵∠ABC＝2∠E，∴∠E＝∠ABE.∴AB∥EF.(3)若AF平分∠BAD，试说明：∠BAD＝2∠F.解：∵AB∥EF，∴∠BAF＝∠F.∵AF平分∠BAD，∴∠BAD＝2∠BAF，∴∠BAD＝2∠F.19．如图，DE∥BC，∠1＝∠3，CD⊥AB.(1)试说明：FG⊥AB；解：∵DE∥BC，∴∠1＝∠2.又∵∠1＝∠3，∴∠2＝∠3，∴CD∥FG.又∵CD⊥AB，∴FG⊥AB.(2)若把条件改为FG⊥AB，∠1＝∠3，CD⊥AB，则DE∥BC吗？说明理由；解：DE∥BC，理由如下：∵FG⊥AB，CD⊥AB，∴FG∥CD，∴∠3＝∠2.又∵∠1＝∠3，∴∠1＝∠2，∴DE∥BC.(3)若把条件改为DE∥BC，CD⊥AB，FG⊥AB，则∠1＝∠3吗？解：∠1＝∠3.理由如下：∵DE∥BC，∴∠1＝∠2.又∵CD⊥AB，FG⊥AB，∴FG∥CD，∴∠2＝∠3，∴∠1＝∠3.