2023年福建省厦门市海沧区中考数学适应性试卷（5月份）（含解析）

这是一份2023年福建省厦门市海沧区中考数学适应性试卷（5月份）（含解析），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. −2023的绝对值是( )
A. −12023B. −2023C. 12023D. 2023
2. 如图所示的几何体的主视图是( )
A.
B.
C.
D.
3. 获第十五届中国钢结构金奖的厦门翔安大桥，全长约12300米，主桥于2023年1月17日正式通车.其中12300用科学记数法表示为( )
A. 12.3×103B. 1.23×103C. 1.23×104D. 0.123×105
4. 如图所示天气符号分别表示“冰雹”、“晴”、“雷雨”、“霜冻”，其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
5. 如所示图形中，若PE=PF，能判断点P在∠EOF的平分线上的是( )
A. B.
C. D.
6. 下列算式，能按照“底数不变，指数相乘”计算的是( )
A. a2+aB. a2⋅aC. (a3)2D. a3÷a
7. 如图所示是甲、乙两名同学五次美术素养测试成绩的统计图.比较甲、乙两名同学的成绩，下列说法正确的是( )
A. 甲同学成绩中位数为85，且方差较大B. 甲同学成绩中位数为90，且方差较小
C. 乙同学成绩中位数为85，且方差较大D. 乙同学成绩中位数为90，且方差较小
8. 如图，A，B是数轴上的两点，点E与点A关于原点O对称，以AB为边作正方形ABCD.若点A表示的数为1，正方形ABCD面积为7，则B，E两点之间的距离是( )
A. 7+2B. 7−2C. 7+1D. 7−1
9. 我国古代著作《四元玉鉴》记载“买椽多少”问题：“六贯二百一十钱，倩人去买几株椽.每株脚钱三文足，无钱准与一株椽.”其大意为：现请人代买一批掾，这批椽的价钱为6210文.如果每株掾的运费是3文，那么少拿一株掾后，剩下的掾的运费恰好等于一株掾的价钱.根据题意可列方程3(x−1)=6210x，其中x表示( )
A. 剩余掾的数量B. 这批掾的数量C. 剩余椽的运费D. 每株掾的价钱
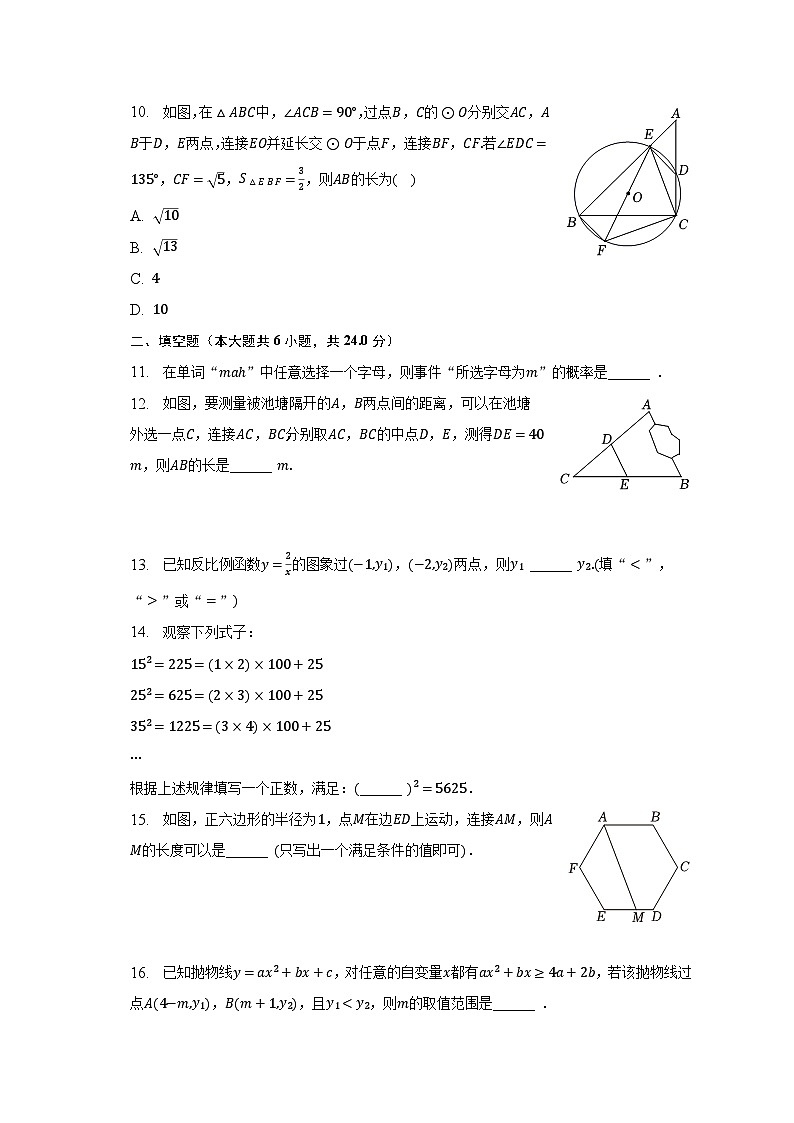
10. 如图，在△ABC中，∠ACB=90°，过点B，C的⊙O分别交AC，AB于D，E两点，连接EO并延长交⊙O于点F，连接BF，CF.若∠EDC=135°，CF= 5，S△EBF=32，则AB的长为( )
A. 10
B. 13
C. 4
D. 10
二、填空题（本大题共6小题，共24.0分）
11. 在单词“mah”中任意选择一个字母，则事件“所选字母为m”的概率是______ ．
12. 如图，要测量被池塘隔开的A，B两点间的距离，可以在池塘外选一点C，连接AC，BC，分别取AC，BC的中点D，E，测得DE=40m，则AB的长是______ m.
13. 已知反比例函数y=2x的图象过(−1,y1)，(−2,y2)两点，则y1 ______ y2.(填“<”，“>”或“=”)
14. 观察下列式子：
152=225=(1×2)×100+25
252=625=(2×3)×100+25
352=1225=(3×4)×100+25
⋯
根据上述规律填写一个正数，满足：(______ )2=5625．
15. 如图，正六边形的半径为1，点M在边ED上运动，连接AM，则AM的长度可以是______ (只写出一个满足条件的值即可)．
16. 已知抛物线y=ax2+bx+c，对任意的自变量x都有ax2+bx≥4a+2b，若该抛物线过点A(4−m,y1)，B(m+1,y2)，且y1三、解答题（本大题共9小题，共86.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题8.0分)
解不等式组：x+2≤3,①1+2x3>x−1.②
18. (本小题8.0分)
如图，在▱ABCD中，AB=FA，E是AF上一点，且AE=FD.求证：AD=BE．
19. (本小题8.0分)
先化简，再求值：(1+1m−2)÷m2−12m−4，其中m= 2−1．
20. (本小题8.0分)
“双减”政策颁布后，学校开展了延时服务，并增加体育锻炼时间.某体育用品商店抓住商机，购进一批乒乓球拍和羽毛球拍进行销售，其进价和售价如表所示．
某班甲体育小组购买2套乒乓球拍和1套羽毛球拍共花费160元，乙体育小组购买1套乒乓球拍和2套羽毛球拍共花费170元．
(1)求出a，b的值；
(2)根据销售情况，商店决定再次购进300套球拍，且购进的乒乓球拍套数不少于羽毛球拍套数的一半.若这批球拍的进价和售价均不变，且能够全部售完，如何购货才能获利最大？
21. (本小题8.0分)
如图，已知⊙O的半径为2，AB是⊙O的直径，点P是AB延长线上一点.以PO为边作△OPC，使得PC=PO，OC=4，OC与⊙O的交点为D，连接AC，PD．
(1)判断直线DP和⊙O位置关系；
(2)若BD的长为3π5，AC=AP，延长PD交AC于点E，求证：EA=EP．
22. (本小题10.0分)
据统计，2021年全国共发生273098起交通事故，其中有一部分是车辆在右转时抢行造成的.一般情况下，车辆右转弯的速度不超过30km/h时为安全车速.如图1，在车辆转弯的情况下，当方向盘转到极限位置，汽车以最低稳定车速行驶时，外侧转向轮B的中心平面在水平路面上滚过的轨迹圆半径BC称为汽车最小转弯半径．
(1)已知某车在低速转弯时，图1中A处的轮胎行进方向与AC垂直，轴距AB为2.4米.方向盘转到极限时，B处车轮方向偏离27°，轮胎前进方向与BC垂直.求该车右转弯时最小转弯半径BC的长.(结果保留2位小数.参考数据：sin27°≈0.45，cs27°≈0.89，tan27°≈0.51)
(2)某校开展“遵守交通法，安全你我他”的宣传活动.九年(1)班数学兴趣小组在某一时段，随机对某一路口右转弯车辆的车速情况进行调查统计，并绘制成图2，图3两幅统计图．
①求这些车辆右转弯的平均速度，并将图3的条形统计图补充完整：
②估计同一时段有200辆车经过该路口右转弯时，属于安全车速的车辆数．
23. (本小题10.0分)
如图，在平面直角坐标系xOy中，点A的坐标为(6,0)，B是y轴上一点．
(1)在线段AB上求作点M，使得△AMO∽△AOB(要求：尺规作图，不写作法，保留作图痕迹)；
(2)在(1)的条件下，AB=4AM，OC是△AOB的中线，过点M的直线交OC于点D，交x轴于点F，当MO=MF时，求点D的坐标．
24. (本小题12.0分)
在矩形ABCD中，E是边CD上一点．
(1)如图1，点D，F关于直线AE对称.平移线段DE，使点E与点F重合，设点D的对应点为G.画出示意图，判断四边形DEFG的形状并证明；
(2)如图2，若DE=k⋅DC(k为常数)，H是矩形内的动点，且满足EH=ED，若点H在运动的过程中，存在线段BH长度最小时，点D，H恰好关于直线AE对称的情形，请探究矩形ABCD的边AD与CD满足的数量关系.(用含k的式子表示)
25. (本小题14.0分)
已知抛物线C1：y=−x2−2x−1，抛物线C2经过点A(−1,0)，B(m+1,0)(m>0)，E为抛物线C2的顶点，M(xM,0)是x轴正半轴上的点．
(1)若E在抛物线C1上，求点E的坐标；(用含m的式子表示)
(2)若抛物线C2：y=x2−mx+n，与y轴交于点C．
①点D(m,yD)在抛物线C2上，当AM=AD，xM=5时，求m的值；
②若m=2，F是线段OB上的动点，过F作GF⊥CF交线段BC于点G，连接CE，GE，求△CGE面积的最小值．
答案和解析
1.【答案】D
【解析】解：|−2023|=2023，
故选：D．
根据绝对值的定义进行计算即可．
本题考查绝对值，理解绝对值的定义是正确解答的前提．
2.【答案】D
【解析】解：从正面看，可得选项D的图形．
故选：D．
找到从正面看所得到的图形即可，注意所有的棱都应表现在主视图中．
本题考查了三视图的知识，主视图是从物体的正面看得到的视图；注意看得到的棱画实线，看不到的棱画虚线．
3.【答案】C
【解析】解：12300=1.23×104．
故选：C．
把一个大于10的数记成a×10n的形式，其中a是整数数位只有一位的数，n是正整数，这种记数法叫做科学记数法，由此即可得到答案．
本题考查科学记数法—表示较大的数，关键是掌握用科学记数法表示数的方法．
4.【答案】B
【解析】解：A、该图形是轴对称图形，但不是中心对称图形，故本选项不符合题意；
B、该图形既是轴对称图形又是中心对称图形，故本选项符合题意；
C、该图形是中心对称图形，但不是轴对称图形，故本选项不符合题意；
D、该图形是轴对称图形，但不是中心对称图形，故本选项不符合题意．
故选：B．
根据轴对称图形和中心对称图形的定义，逐项判断即可求解．
本题主要考查了轴对称图形和中心对称图形的定义，熟练掌握如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形；在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形是解题的关键．
5.【答案】D
【解析】解：∵到角两边的距离相等的点在角平分线上，
∴符合题意的是D．
故选：D．
根据到角两边的距离相等的点在角平分线上进行判断即可．
本题主要考查角平分线的性质，解答的关键是熟记到角两边的距离相等的点在角平分线上．
6.【答案】C
【解析】解：能按照“底数不变，指数相乘”计算的是(a3)2．
故选：C．
直接利用同底数幂的乘除运算、幂的乘方运算法则判断得出答案．
此题主要考查了幂的乘方运算、同底数幂的乘除运算，正确掌握相关运算法则是解题关键．
7.【答案】B
【解析】解：由折线图可知，甲同学五次测试成绩从小到大排列为：85，85，90，90，95，所以中位数为90；
乙同学五次测试成绩从小到大排列为：80，80，90，95，100，所以中位数为90；
甲同学五次测试成绩与乙同学相比，分布比较集中，各数据偏离平均数较小，即波动较小，所以方差较小．
故选：B．
根据中位数和方差的定义进行判断即可．
本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．也考查了折线统计图与中位数．找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数．
8.【答案】A
【解析】解：根据题意得，
AB= 7，
∵E与点A关于原点O对称，点A表示的数为1，
∴E点表示的数为−1，
∴AE=2，
∴BE之间的距离为BE=AE+AB=2+ 7．
故选：A．
根据题意求出点E表示的数，求出AB边的长，即可求解．
本题考查了实数与数轴的简单应用，解题的关键是求出点E和线段AB的长，题目比较简单．
9.【答案】B
【解析】解：∵每株掾的运费是3文，那么少拿一株掾后，剩下的掾的运费恰好等于一株掾的价钱，
∴3(x−1)表示少拿一株掾后的运费，6210x表示一株掾的价钱，
∴x表示这批掾的数量．
故选：B．
分析方程，可得出3(x−1)表示少拿一株掾后的运费，6210x表示一株掾的价钱，进而可得出x表示这批掾的数量．
本题考查了由实际问题抽象出一元二次方程，根据所列方程，找出未知数x的意义是解题的关键．
10.【答案】C
【解析】解：∵四边形BCDE内接于⊙O，且∠EDC=135°，

∴∠EFC=∠ABC=180°−∠EDC=45°，
∵∠ACB=90°，
∴△ABC是等腰直角三角形，
∴AC=BC，
又∵EF是⊙O的直径，
∴∠EBF=∠ECF=∠ACB=90°，
∴∠BCF=∠ACE，
∵四边形BECF是⊙O的内接四边形，
∴∠AEC=∠BFC，
∴△ACE≌△BCF(ASA)，
∴AE=BF，
∵Rt△ECF中，CF= 5、∠EFC=45°，
∴EF2=10．
∵S△EBF=32，
∴12BF⋅BE=32，
∴BF⋅BE=3，
∴2BF⋅BE=6，
∴AE2+BE2=BF2+BE2=EF2=10，
∴(AE+BE)2=AE2+BE2+2BF⋅BE=16，
∴AE+BE=4．
故选：C．
由四边形BCDE内接于⊙O知∠EFC=∠ABC=45°，据此得AC=BC，由EF是⊙O的直径知∠EBF=∠ECF=∠ACB=90°及∠BCF=∠ACE，再根据四边形BECF是⊙O的内接四边形知∠AEC=∠BFC，从而证△ACE≌△BCF得AE=BF，根据Rt△ECF是等腰直角三角形知EF2=10，继而可得答案．
本题主要考查圆周角定理，解题的关键是掌握圆内接四边形的性质、圆周角定理、全等三角形的判定与性质及勾股定理．
11.【答案】13
【解析】解：“所选字母为m”的概率是：13．
故答案为：13．
单词“mah”中共有3个字母，“m”出现1次，再利用概率公式进行计算即可．
此题主要考查了概率公式，关键是掌握随机事件A的概率P(A)=事件A可能出现的结果数所有可能出现的结果数．
12.【答案】80
【解析】解：∵点D，E分别是AC，BC的中点，
∴DE是△ABC的中位线，
∴AB=2DE=2×40=80米．
故答案为：80．
先判断出DE是△ABC的中位线，再根据三角形的中位线平行于第三边并且等于第三边的一半可得AB=2DE，问题得解．
本题考查了三角形的中位线平行于第三边并且等于第三边的一半，熟记定理并准确识图是解题的关键．
13.【答案】<
【解析】解：∵反比例函数y=2x的图象经过第一、三象限，
∴A(−1,y1)，(−2,y2)在第三象限，
∵−1>−2，
∴y1故答案为：<．
根据反比例函数的性质得函数y=2x的图象过第一、三象限，在同一象限内，y随x的增大而减小，从而得出y1与y2的大小关系．
本题考查了反比例函数图象上点的坐标特征，熟知反比例函数的性质是解答此题的关键．
14.【答案】75
【解析】解：根据规律152=225=(1×2)×100+25，
252=625=(2×3)×100+25，
352=1225=(3×4)×100+25，
(10n+5)2=n(n+1)×100+25
⋅⋅⋅
752=5625=(7×8)×100+25，
则752=5625．
根据题意总结出一般规律(10n+5)2=n(n+1)×100+25，然后代入求解即可．
本题考查了规律型：数字的变化类和有理数数的混合运算，掌握个位数字是5的数的平方的计算规律．
15.【答案】1.8(答案不唯一，只要符合 3≤AM≤2即可)．
【解析】解：设正六边形的中心为O，连接OF，OE，AE，AD，

根据正六边形的性质得：AD经过点O，∠AOE=360°÷6=60°，OA=OF=OE=OD=1，
∴△AOF为等边三角形，
∴AF=OA=OF=1，∠OFA=60°
同理：△OEF为等边三角形，
∴∠OFE=60°
∴∠OFA=∠OFE=60°，
又AF=EF，
∴AE⊥OF，
∴FT=OT=12OF=0.5，AT=EF，
在Rt△AFT中，AF=1，FT=0.5，
由勾股定理得：AT= AF2−FT2= 32，
∴AE=2AT= 3，
又∵OA=OD=1，
∴AD=2，
∵AM在边ED上运动，
∴AE≤AM≤AD，
即： 3≤AM≤2，
∴AH=1.8．
故答案为：1.8(答案不唯一，只要符合 2≤AM≤2即可)．
设正六边形的中心为O，连接OA，OF，OE，AE，AD，根据正六边形的性质得△AOF和△OEF为等边三角形，然后可由勾股定理求出AT，进而得AE= 3，再求出AD=2，根据AM在边ED上运动得 3≤AM≤2，最后在这个的范围内取一个值即可．
此题主要考查了正多边形的性质，等边三角形的性质，等腰三角形的性质，勾股定理等，解答此题的关键是熟练掌握正多边形的性质，中心角、半径等概念．
16.【答案】m>32
【解析】解：∵ax2+bx≥4a+2b，
可知当x=2时，ax2+bx=4a+2b，
ax2+bx+c≥4a+2b+c，
∴当x=2时，抛物线函数值最小，
∴x=2是对称轴，a>0，开口向上，
∵y1∴|4−m−2|<|m+1−2|，
∴|2−m|<|m−1|
∴(2−m)2<(m−1)2，
∴m2−4m+4∴−2m<−3，
∴m>32．

故答案为：m>32．
根据题意可判断出抛物线的对称轴，开口方向，再由y1本题考查了二次函数的图象与性质，解题的关键是判断出抛物线的对称轴及开口方向．
17.【答案】解：由①可得：x≤1，
由②可得：x<4，
∴不等式组的解集为x≤1．
【解析】先分别求出两个不等式的解集，进一步求出公共解集．
本题主要考查了学生解不等式组的知识，同大取大，同小取小，大小小大中间找，大大小小无处找．
18.【答案】证明：∵四边形ABCD是平行四边形，
∴AB//CD，
∴∠DFA=∠EAB，
在△ABE与△AFD中，
AE=DF∠DFA=∠EABAB=AF，
∴△ABE≌△AFD(SAS)，
∴AD=BE．
【解析】根据平行四边形的性质得出AB//CD，进而利用SAS证明△ABE与△AFD全等，进而利用全等三角形的性质解答即可．
此题考查平行四边形的性质、全等三角形的判定和性质，关键是根据平行四边形的性质得出AB//CD解答．
19.【答案】解：原式=(m−2m−2+1m−2)÷(m+1)(m−1)2(m−2)，
=m−1m−2⋅2(m−2)(m+1)(m−1)，
=2m+1．
当m= 2−1时，原式=2 2−1+1= 2．
【解析】先根据分式的运算法则对原式进行化简，再把m的值代入化简结果计算即可．
本题考查的是分式的化简求值，熟知分式混合运算的法则是解题的关键．
20.【答案】解：(1)根据题意得：2a+b=160a+2b=170，
解得：a=50b=60，
答：a、b的值分别是50元、60元；
(2)设购进乒乓球拍x套，羽毛球拍(300−x)套．总利润为y元，
由题意得：x≥12(300−x)，
解得：x≥100，
∵y=(50−35)x+(60−40)(300−x)
=−5x+6000，
∵−5<0，
∴y随x的增大而减小，
∴当x=100时，y最大，且最大值为：−5×100+6000=5500(元)，
此时300−x=200，
答：购进乒乓球拍100套，羽毛球拍200套，获利最大，最大利润为5500元．
【解析】(1)根据购进2套乒乓球拍和1套羽毛球拍需花费160元，购进4套乒乓球拍和3套羽毛球拍需花费170元，列出方程组，解方程组即可；
(2)根据总利润=乒乓球拍的利润+羽毛球拍的利润列出函数解析式，再根据购进乒乓球拍的套数不少于羽毛球拍套数的12求出自变量的取值范围，再根据函数的性质求最值即可．
本题考查一次函数和二元一次方程组的应用，解题的关键是仔细审题，找到等量关系列出函数解析式和列出方程组．
21.【答案】(1)解：直线DP和⊙O相切，
理由：∵OD=2，OC=4，
∴OD=CD，
∵PO=PC，
∴PD⊥OC，
∵OD是⊙O的半径，
∴直线DP和⊙O相切；
(2)证明：设∠BOD=n°，
∵BD的长为3π5，
∴n⋅π×2180=3π5，
解得n=54，
∴∠BOD=54°，
∵OP=PC，
∴∠PCO=∠POC=54°，
∴∠APC=180°−∠PCO−∠POC=72°，
∵AP=AC，
∴∠ACP=∠APC=72°，
∴∠A=36°，
∴∠OPD=∠CPD=12×(180°−54°−54°)=36°，
∴∠A=∠APE，
∴AE=PE．
【解析】(1)根据已知条件得到OD=CD，根据等腰三角形的性质得到PD⊥OC，根据切线的判定定理即可得到结论；
(2)设∠BOD=n°，根据弧长公式得到n=54，求得∠BOD=54°，根据等腰三角形的性质得到∠PCO=∠POC=54°，求得∠A=36°，得到∠A=∠APE，根据等腰三角形的判定定理即可得到结论．
本题考查了直线与圆的位置关系，等腰三角形的判定和性质，熟练掌握切线的判定定理是解题的关键．
22.【答案】解：(1)在Rt△ABC中，sin∠ACB=ABAB，
∴0.45=2.4BC，
∴BC=5.33(米)，
答：该车右转弯时最小转弯半径BC的长5.33米；
(2)①总数=6÷30%=20(辆)，
速度为30km/h的数量为20×20%=4(辆)，
速度为35km/h的数量为20−2−6−5−4=3(辆)，
∴平均速度=120(2×15+6×20+5×25+4×30+3×35)=25km/h．
条形图如图所示：

②200×2+6+520=130(辆)，
答：估计200辆车经过该路口右转弯时，属于安全车速的车辆数为130辆．
【解析】(1)解直角三角形求出BC即可；
(2)①求出速度为30，35km/h的数量，再根据平均数的定义求出平均速度，可得结论；
②用样本估计总体的思想思考问题．
本题考查轨迹，解直角三角形，条形统计图等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
23.【答案】解：(1)如图，点M即为所求；

(2)∵△AMO∽△AOB，
∴AO：AB=AM：AO，
∴OA2=AM⋅AB，
∵A(6,0)，
∴OA=6，
∵AB=4AM，
∴AM×4AM=36，
∴AM=3，AB=12，
∴OB= AB2−AO2= 122−62=6 3，
∴B(0,6 3)，
∵AC=BC，
∴C(3,3 3)，
∴直线OC的解析式为y= 3x，
∵OM⊥AB，
∴12⋅OA⋅OB=12⋅OM⋅AB，
∴OM=6×6 312=3 3，
∴M(92,3 32)，
∵MO=MF，
∴F(9,0)，
直线MF的解析式为y=− 33x+3 3，
由y=− 33x+3 3y= 3x，解得x=94y=9 34，
∴D(94,9 34).
【解析】(1)作OM⊥AB于点M即可；
(2)求出直线OC，直线MF的解析式，构建方程组求解．
本题考查作图−相似变换，一次函数的应用等知识，解题的关键是学会构建一次函数确定交点坐标．
24.【答案】解：(1)如图，

四边形DEFG为菱形，证明如下：
连接DF，EF，DG，
∵点D、F关于直线AE对称，
∴AE垂直平分DF，
∴ED=EF，
∵DE平移至点E与点F重合，
∴DG//EF，且DG=EF，
∴四边形DGFE为平行四边形．
又∵ED=EF，
∴四边形DGFE为菱形．
(2)∵EH=ED，
∴当E、H、B三点共线时，BH长度最小，
此时点D、H关于直线AE对称，
∴AE为DH的垂直平分线，
∴AD=AH，ED=EH，
∴△EDA≌△EHA(SSS)，

∴∠AHE=∠ADE=90°，
∴∠AHB=90°，
设CD=a，AD=b，
则DE=ka，CE=(1−k)a，AH=BC=AD=b，AB=CD=a，
在矩形ABCD中，∠ABH+∠EBC=90°，∠C=90°，
∴∠EBC+∠BEC=90°，
∴∠CEB=∠ABH，
又∵∠AHB=∠BCE=90°，AH=BC=b，
∴△ABH≌△BEC(AAS)，
∴BH=CE=(1−k)a，
∴BE=AB=a，
在Rt△BCE中，BE2=CE2+BC2，
即a2=(1−k)2a2+b2，
根据题意知a>0，b>0，0解得b= 2k−k2a，
∴矩形的边AD和CD满足的数量关系为：AD= 2k−k2CD．
【解析】(1)连接DF，EF，DG，根据题意证明四边形DGFE为平行四边形，即可得证．
(2)证明△EDA≌△EHA(SSS)，设CD=a，AD=b，则DE=ka，CE=(1−k)a，AH=BC=AD=b，AB=CD=a，根据矩形的性质证明△ABH≌△BEC(AAS)，利用勾股定理即可求解．
本题考查了四边形的综合应用，解题关键是掌握矩形的性质，全等三角形的性质与判定，勾股定理的应用．
25.【答案】解：(1)∵抛物线C2经过点A(−1,0)，B(m+1,0)(m>0)，
∴抛物线的对称轴为直线x=12m，
∵E在抛物线C1上，
∴y=−14m2−m−1，
∴E(12m,−14m2−m−1)；
(2)①∵抛物线C2：y=x2−mx+n经过点A(−1,0)，
∴1+m+n=0，
∴抛物线的解析式为y=x2−mx−1−m，
∵点D(m,yD)在抛物线C2上，
∴yD=−m−1，
∴D(m,−m−1)，
∵m>0，
∴m>12m>0，−m−1<0，
∴点D在第四象限，在直线x=12m的右侧，
过D点作DH⊥x轴交于H点，则H(m,0)，
∴AH=m+1，DH=m+1，
∴AH=DH，
在Rt△ADH中，∠ADH=∠DAH=45°，
∴AD= 2AH，
∵AM=AD，xM=5，
∴5+1= 2(m+1)，
解得m=3 2−1；
②过点G作MG⊥x轴交于点M，过点E作NE//y轴交BC于点N，
由(1)可知，当m=2时，抛物线C2的顶点E(1,−4)，
∴抛物线C2的解析式为y=x2−2x−3，
∴C(0,−3)，
∵B(3,0)，
设直线BC的解析式为y=kx−3，
∴3k−3=0，
解得k=1，
∴直线BC的解析式为y=x−3，
∴N(1,−2)，
设G(t,t−3)，F(x,0)，
∴S△CGE=S△NEC+S△NEG
=12×NE×(xG−xC)
=t，
∵∠CFG=90°，
∴∠FGM+∠GFM=90°，∠GFM+∠OFC=90°，
∴∠OFC=∠FGM，
∴△OFC∽△FGM，
∴MFMG=OCOF，即t−x3−t=3x，
整理得，x2−tx+9−3t=0，
令y=x2−tx+9−3t，(0∵当x=3时，y=18−6t>0，对称轴x=12t在y轴右侧，
∴要保证x2−tx+9−3t=0在0解得t≥6 2−6或t≤−6 2−6，
∴S△CGE=t≥6 2−6，
∴△CGE面积的最小值为6 2−6．
【解析】(1)根据抛物线的对称性求出抛物线的对称轴，再由E点在抛物线C1上，求E点坐标即可；
(2)①过D点作DH⊥x轴交于H点，则H(m,0)，判断出△ADH是等腰直角三角形，则AD= 2AH，又有AM=AD，xM=5，得到方程5+1= 2(m+1)，求出m=3 2−1；
②过点G作MG⊥x轴交于点M，过点E作NE//y轴交BC于点N，求出直线BC的解析式为y=x−3，可知N(1,−2)，设G(t,t−3)，F(x,0)，则S△CGE=S△NEC+S△NEG=t，证明△OFC∽△FGM，可得x2−tx+9−3t=0，令y=x2−tx+9−3t，(0本题考查二次函数的图象及性质，熟练掌握二次函数的图象及性质，三角形相似的判定及性质，直角三角形的性质是解题的关键．
进价
售价
乒乓球拍(元/套)
35
a
羽毛球拍(元/套)
40
b