初中数学湘教版七年级下册6.2 方差公开课教案设计

6.2方差

【知识与技能】

1.了解方差的定义和计算公式.

2.理解方差概念的产生和形成的过程.

3.会用方差计算公式来比较两组数据的波动大小.

【过程与方法】

经历探索极差、方差的应用过程，体会数据波动中的极差、方差的求法以及区别，积累统计经验.

【情感态度】

培养学生的统计意识，形成尊重事实、用数据说话的态度，认识数据处理的实际意义.

【教学重点】

方差产生的必然性和应用方差公式解决实际问题，掌握其求法.

【教学难点】

理解方差公式，应用方差对数据波动情况进行比较、判断.

一、情景导入，初步认知

我们在前面学习了平均数、中位数、众数，它们各有什么优缺点？

【教学说明】通过复习，为本节课的学习作铺垫.

二、思考探究，获取新知

1.刘亮和李飞参加射击训练，成绩如下：

刘亮：7、8、8、9、7、8、8、9、7、9

李飞：6、8、7、7、8、9、10、7、9、9

(1)两人的平均成绩分别是多少？

(2)如何反映这两组数据与其平均数的偏离程度？

(3)谁的成绩更稳定？

解：刘亮的成绩的平均数是：=8.0；

李飞的成绩的平均数是：=8.0.

即两人的平均成绩相同.

为了直观地看出这两组数据与其平均数的偏离程度，我们用下图来表示数据的分布情况.

由上面两幅图，可以发现刘亮的射击成绩多集中在平均成绩8环附近，而李飞的射击成绩与其平均成绩偏差较大.一组数据中的数与这组数据的平均数的偏离程度是数据的一个重要特征，它反映了一组数据的离散程度或波动大小.

2.那么如何找到一个特征值来反映一组数据与其平均数的离散程度呢？

【归纳结论】为了反映一组数据的离散程度，可以采用很多方法，统计中常用以下做法：设一组数据为x1,x2,……,xn,各数据与平均数x之差的平方的平均值，叫做这组数据的方差，记作：s2.

方差公式：

【教学说明】学生理解和记忆这个公式都会有一定困难，以致应用时常常出现计算的错误，为突破这一难点，教师可以直接对方差公式作分析和解释，波动大小指的是与平均数之间差异，那么用每个数据与平均值的差完全平方后便可以反映出每个数据的波动大小，整体的波动大小可以通过对每个数据的波动大小求平均值得到.

3.利用公式分别计算出刘亮与李飞的射击成绩的方差.

如何从方差上来看一组数据的波动情况呢？

【归纳结论】一组数据的方差越小，说明这组数据离散程度或波动的程度就越小，这组数据也就越稳定.

三、运用新知，深化理解

1.见教材P150例题.

2.甲、乙两位同学在几次数学测验中，各自的平均成绩都是88分，甲的方差为0.62，乙的方差为0.73，则(A)

A.甲成绩比乙成绩稳定

B.乙成绩比甲成绩好

C.甲、乙成绩一样

D.甲、乙成绩无法比较

3.在一次射击练习中，甲、乙两人前5次射击成绩分别为(单位：环)：

甲：10  8 10 10  7

乙：7 10  9  9 10

则这次练习中，甲、乙两人方差s甲2与s乙2的大小关系是(A)

A.s甲2>s乙2  B.s甲2<s乙2

C.s甲2=s乙2  D.无法确定

4.已知一个样本的方差，其平均数为.

答案：30.

5.从甲、乙两种玉米苗中各抽10株，分别测得它们的株高(单位：cm)如下：

甲：25 41 40 37 22 14 19 39 21 42

乙：27 16 44 27 44 16 40 40 16 40

问：(1)哪种玉米的苗长得高？

(2)哪种玉米的苗长得齐？

解：(1)x甲=(25+41+40+37+…+42)=30(cm)

x乙=(27+16+44+27+…+40)=31(cm)

因为，所以乙种玉米的苗长得高.

(2)s甲2=(25-30)2+(41-30)2+…+(42-30)2］=×1042=104.2(cm2).

s乙2=(27-31)2+(16-31)2+…+(40-31)2］=×1288=128.8(cm2).

因为s甲2<s乙2，所以甲种玉米的苗长得齐.

6.两台机床同时生产直径为10个单位的零件，为了检验产品的质量，质检员从两台机床的产品中各抽出5件进行测量，结果如下：

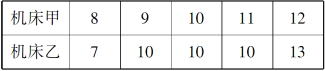
如果你是质检员，在收集到上述数据后，你将利用哪些统计知识来判断这两台机床生产的零件的质量优劣.

解：(1)由于x甲=x乙=10，因此平均直径反映不出两台机床生产出的零件的质量优劣.

(2)s2甲=2，s2乙=3.6，由于s2甲<s2乙，因此，从产品质量稳定性的角度考虑，甲机床生产的零件质量更符合要求；

(3)甲机床只有一个零件的直径是10，而乙机床有3个零件的直径是10，从众数角度看，乙机床生产出的零件符合要求.

7.甲、乙两人在相同条件下各射靶10次，每次射靶的成绩情况如折线图所示：

(1)请填写下表：

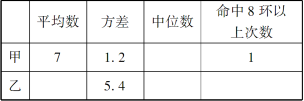
(2)请从下列四个不同的角度对这次测试结果进行分析.

①从平均数和方差相结合看；

②从平均数和中位数相结合看(分析谁的成绩好些)；

③从平均数和命中9环以上的次数相结合看(分析谁的成绩好些)；

④从折线图上两人射击命中环数的走势看(分析谁更有潜力).

解：(1)如下表：

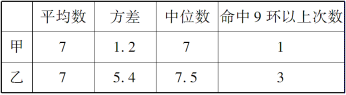
(2)①∵平均数相同，s2甲<s2乙，∴甲成绩比乙稳定;

②∵平均数相同，甲的中位数<乙的中位数，∴乙的成绩比甲好些;

③∵平均数相同，命中9环以上的次数甲比乙少，∴乙的成绩比甲好些;

④甲成绩在平均数上下波动，而乙处于上升势头，从第4次以后就没有比甲少的情况发生，乙较有潜力.

【教学说明】学生独立完成，教师适当提示.

四、师生互动,课堂小结

(1)知识小结：

其中，x1，x2…xn等代表一组数据，x代表数据的平均值，n代表数据的个数.

(2)方法小结：

求一组数据方差的方法：先求平均数，再利用方差公式求方差，也可以用计算器求方差.

1.布置作业:教材第152页“习题6.2”中第3、4题.

2.完成同步练习册中本课时的练习.

通过这节课的教学，让我深刻地体会到我们要充分相信学生，给学生以最大的自主探索空间，让学生经历数学知识的探究过程，这样既能让学生自主获取数学知识与技能，而且还能让学生达到对所学知识的深层次理解，更主要的是能让学生在探究过程中学习科学研究的方法，从而增强学生的自主意识，培养学生的探索精神和创新思维.