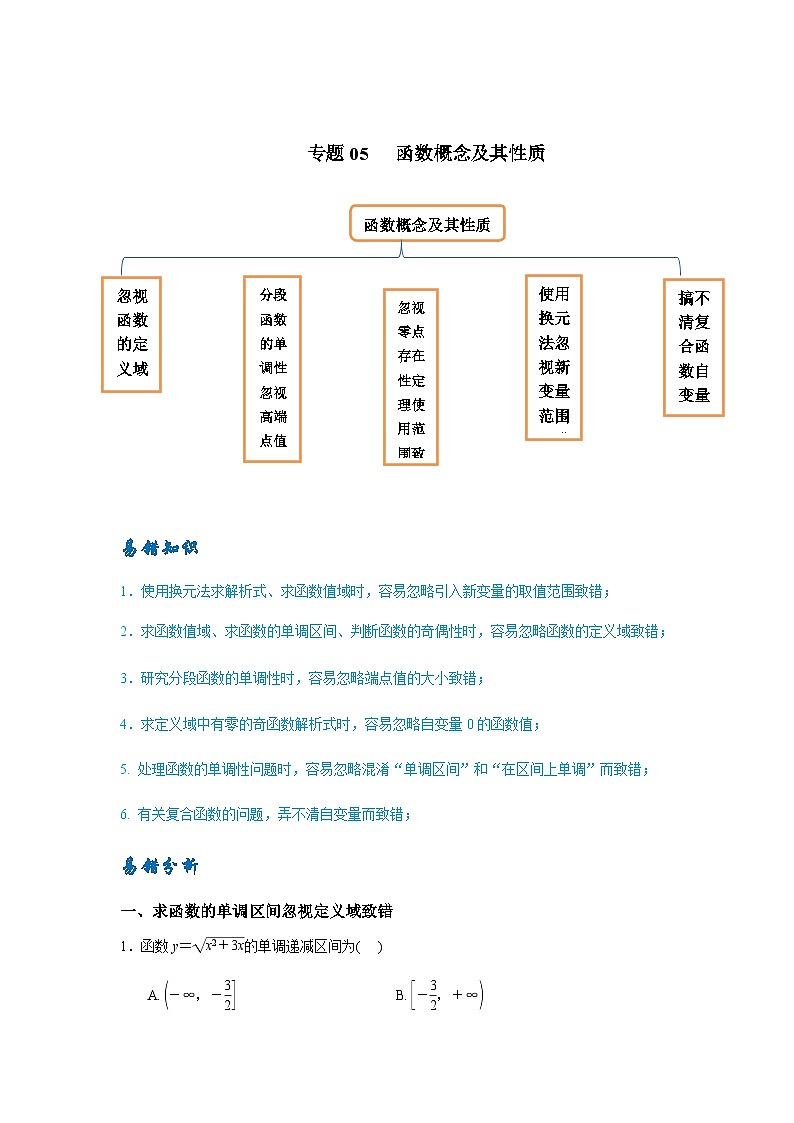
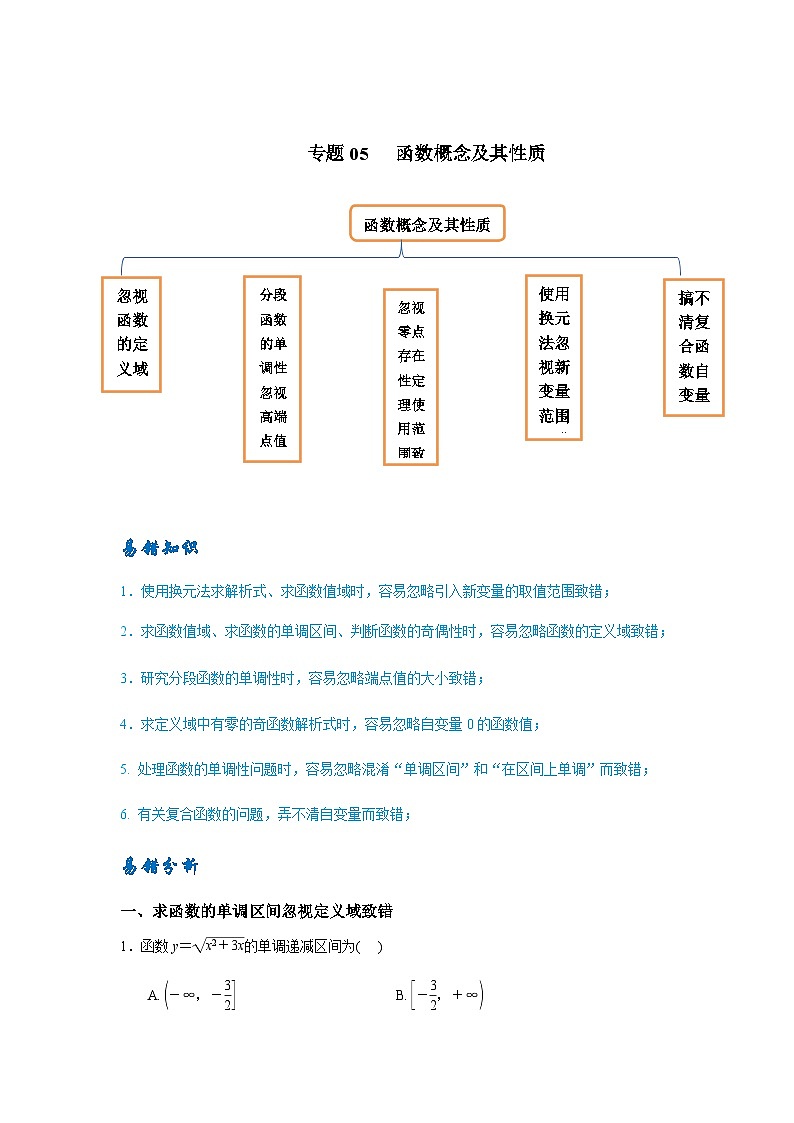
易错点05 函数概念及其性质-备战2024年高考数学考试易错题（新高考专用）

这是一份易错点05 函数概念及其性质-备战2024年高考数学考试易错题（新高考专用），文件包含易错点05函数概念及其性质-备战2024年高考数学易错题新高考专用解析版docx、易错点05函数概念及其性质-备战2024年高考数学易错题新高考专用原卷版docx等2份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。

函数概念及其性质
忽视函数的定义域致错
分段函数的单调性忽视高端点值致错
使用换元法忽视新变量范围致错
搞不清复合函数自变量致错
忽视零点存在性定理使用范围致错
易错知识
1．使用换元法求解析式、求函数值域时，容易忽略引入新变量的取值范围致错；
2．求函数值域、求函数的单调区间、判断函数的奇偶性时，容易忽略函数的定义域致错；
3．研究分段函数的单调性时，容易忽略端点值的大小致错；
4．求定义域中有零的奇函数解析式时，容易忽略自变量0的函数值；
5. 处理函数的单调性问题时，容易忽略混淆“单调区间”和“在区间上单调”而致错；
6. 有关复合函数的问题，弄不清自变量而致错；
易错分析
一、求函数的单调区间忽视定义域致错
1．函数y＝eq \r(x2＋3x)的单调递减区间为( )
A.eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(3,2))) B.eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(3,2)，＋∞))
C．[0，＋∞) D．(－∞，－3]
【错解】选A 令t＝x2＋3x，y＝eq \r(x2＋3x)是由y＝eq \r(t)与t＝x2＋3x复合而成，又外层函数y＝eq \r(t)在[0，＋∞)上单调递增，内层函数t＝x2＋3x在eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(3,2))) 上单调递减，在eq \b\lc\[\rc\)(\a\vs4\al\c1(－\f(3,2)，＋∞))上单调递增，根据复合函数同增异减的原则可知，函数y＝eq \r(x2＋3x)的单调递减区间为eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(3,2))) ．
【错因】没有考虑函数y＝eq \r(x2＋3x)的定义域，
【正解】选D 由题意，x2＋3x≥0，可得x≤－3或x≥0，函数y＝eq \r(x2＋3x)的定义域为
(－∞，－3]∪[0，＋∞)．令t＝x2＋3x，则外层函数y＝eq \r(t)在[0，＋∞)上单调递增，内层函数
t＝x2＋3x在(－∞，－3]上单调递减，在[0，＋∞)上单调递增，所以，函数y＝eq \r(x2＋3x)的单调递减区间为(－∞，－3]．
二、判断函数的奇偶性忽视定义域致错
2．判断函数f(x)＝eq \r(\f(1－x,1＋x))的奇偶性：
【错解】
，所以函数f(x)＝eq \r(\f(1－x,1＋x))为偶函数。
【错因】没有考虑函数f(x)＝eq \r(\f(1－x,1＋x))的定义域，
【正解】因为f(x)有意义，则满足eq \f(1－x,1＋x)≥0，所以－1所以f(x)为非奇非偶函数．
三、有关分段函数的不等式问题忽视定义域致错
3．设函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋12，x<1，,4－\r(x－1)，x≥1，)) 则使得f(x)≥1的自变量x的取值范围为__________．
【错解】由已知及f(x)≥1可得．(x＋1)2≥1或4－eq \r(x－1)≥1，
由(x＋1)2≥1⇒x≤－2或x≥0，由4－eq \r(x－1)≥1，即eq \r(x－1)≤3，所以1≤x≤10.
综上所述，x∈[1,10]．
【错因】没有考虑函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋12，x<1，,4－\r(x－1)，x≥1，))的定义域，
【正解】因为f(x)是分段函数，所以f(x)≥1应分段求解．
当x<1时，f(x)≥1⇒(x＋1)2≥1⇒x≤－2或x≥0，所以x≤－2或0≤x<1.
当x≥1时，f(x)≥1⇒4－eq \r(x－1)≥1，即eq \r(x－1)≤3，所以1≤x≤10.
综上所述，x∈(－∞，－2]∪[0,10]．
四、有关抽象函数的不等式问题忽视定义域致错
4．设a∈R，已知函数y＝f(x)是定义在[－4,4]上的减函数，且f(a＋1)>f(2a)，则a的取值范围是( )
A．[－4,1) B．(1,4] C．(1,2] D．C．（1，＋∞)
【错解】∵y＝f(x)是定义在[－4,4]上的减函数，且f(a＋1)>f(2a)，∴a＋1<2a，解得1【错因】没有考虑函数y＝f(x)的定义域，
【正解】∵函数y＝f(x)是定义在[－4,4]上的减函数，且f(a＋1)>f(2a)，∴－4≤a＋1<2a≤4，
解得1五、有关分段函数的单调性问题忽视端点值致错
5. 已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋1，x<1，,x2－2ax，x≥1))在R上单调递增，则实数a的取值范围为________．
【错解】要使f(x)在R上单调递增，必须满足：f(x)在(－∞，1)上单调递增，f(x)在(1，＋∞)上单调递增；又x≥1时，，作出大致图象如图所示．结合图象可知a≤1,故实数a的取值范围为(－∞，1].
【错因】没有考虑端点值2与的大小关系，
【正解】要使f(x)在R上单调递增，必须满足三条：第一条：f(x)在(－∞，1)上单调递增；
第二条：f(x)在(1，＋∞)上单调递增；第三条：(x2－2ax)|x＝1≥(x＋1)|x＝1.
作出大致图象如图所示．结合图象可知eq \b\lc\{\rc\ (\a\vs4\al\c1(a≤1，,1－2a≥2，))解得a≤－eq \f(1,2).
故实数a的取值范围为eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，－\f(1,2))).
六、有关奇函数的解析式忽视自变量0的函数值致错
6．已知定义在R上的奇函数f(x)，当x>0时，f(x)＝x2＋x－1，则函数f(x)的解析式为_______．
【错解】设x<0，则－x>0，由题意可知f(－x)＝(－x)2－x－1＝x2－x－1，
因为f(x)是R上的奇函数，所以f(x)＝－f(－x)＝－x2＋x＋1.
综上所述，
【错因】没有考虑自变量0的函数值，
【正解】设x<0，则－x>0，由题意可知f(－x)＝(－x)2－x－1＝x2－x－1，
因为f(x)是R上的奇函数，所以f(x)＝－f(－x)＝－x2＋x＋1，且f(0)＝0.
综上所述，f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2＋x－1，x>0，,0，x＝0，,－x2＋x＋1，x<0.))
七、使用换元法忽视新变量的取值范围致错
7．若f(2x)＝4x－2x，则f(x)＝________.
【错解】由题意，f(2x)＝4x－2x＝(2x)2－2x，设t＝2x，则f(t)＝t2－t，所以f(x)＝x2－x.
【错因】没有考虑2x的取值范围，因为2x大于零，所以t大于零，
【正解】由题意，f(2x)＝4x－2x＝(2x)2－2x，设t＝2x>0，则f(t)＝t2－t，t>0，所以f(x)＝x2－x，x>0.
八、忽视零点存在性定理前提条件而致错
8．对于函数f(x)，若f(－1)f(3)<0，则( )
A．方程f(x)＝0一定有实数解 B．方程f(x)＝0一定无实数解
C．方程f(x)＝0一定有两实根 D．方程f(x)＝0可能无实数解
【错解】因为f(－1)f(3)<0，由零点存在性定理知函数f(x)在(－1,3)上必有零点，
故方程f(x)＝0一定有实数解，所以选A。
【错因】零点存在性定理要求f(x)的图象在区间[a，b]上连续。
【正解】选D 因为函数f(x)的图象在(－1,3)上未必连续，所以尽管f(－1)f(3)<0，
但方程f(x)＝0在(－1,3)上可能无实数解．
9．若函数y＝f(x)在区间[a，b]上的图象为一条连续不断的曲线，则下列说法正确的是( )
A．若f(a)f(b)>0，则不存在实数c∈[a，b]，使得f(c)＝0
B．若f(a)f(b)<0，则存在且只存在一个实数c∈[a，b]，使得f(c)＝0
C．若f(a)f(b)>0，则可能存在实数c∈[a，b]，使得f(c)＝0
D．若f(a)f(b)<0，则可能不存在实数c∈[a，b]，使得f(c)＝0
【错解】选A，因为f(－2)f(2)>0，与零点存在性定理f(a)f(b)<0不符，所以不存在实数
c∈[a，b]，使得f(c)＝0。
【错因】零点存在性定理是f(x)在区间[a，b]上存在零点的充分不必要条件。
【正解】选C，取f(x)＝x2－1，区间取为[－2,2]，满足f(－2)f(2)>0，但是f(x)在[－2,2]内存在两个零点－1,1，故A说法错误，C说法正确；取f(x)＝sin x，区间取为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(19π,6)))，满足feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,6)))feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(19π,6)))＝eq \f(1,2)×eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)))＝－eq \f(1,4)<0，但是f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(19π,6)))内存在三个零点π，2π，3π，故B说法错误；根据函数零点存在定理可知，D说法错误．
九、搞不清复合函数的自变量而致错
10．已知f(x2－1)的定义域为[0,3]，则f(2x－1)的定义域是( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(9,2))) B.eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(9,2)))
C.D．eq \b\lc\(\rc\](\a\vs4\al\c1(－∞，\f(9,2)))
【错解】选C ∵f(x2－1)的定义域为[0,3]，∴0≤x≤3，∴0≤x2－1≤3，∴1≤x2≤4，
∴1≤x≤2或－2≤x≤－1，所以1≤2x－1≤2或－2≤2x－1≤－1，
所以1≤x≤或－≤x≤0，则f(2x－1)的定义域是。
【错因】搞不清复合函数的自变量是哪个，f(x2－1)的定义域为[0,3]，是说0≤x≤3。
【正解】选B ∵f(x2－1)的定义域为[0,3]，∴0≤x≤3，∴－1≤x2－1≤8，即f(x)的定义域为
[－1,8]．∴在f(2x－1)中－1≤2x－1≤8，∴0≤x≤eq \f(9,2)，即函数f(2x－1)的定义域为eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(9,2))).
十、搞不清函数图象左右平移规则而致错
10．将函数y＝f(－x)的图象向右平移1个单位长度得到函数________的图象．
【错解】y＝f(－x)的图象向右平移1个单位长度，根据左加右减的原则，可知得到函数f(－x－1)的图象。故答案为y＝f(－x－1)
【错因】函数图象左加右减变换针对的是自变量x,
【正解】y＝f(－x)的图象向右平移1个单位长度，根据左加右减的原则，可知得到函数的图象，故答案为y＝f(－x＋1)
易错题通关
1．已知函数f(x)＝ex－e－x＋x3＋3，若f(a)＝5，则f(－a)＝( )
A．2 B．1 C．－2 D．－5
【答案】B
【解析】设g(x)＝f(x)－3＝ex－e－x＋x3，则g(－x)＝e－x－ex－x3＝－(ex－e－x＋x3)＝－g(x)，所以g(x)是奇函数．因为g(a)＝f(a)－3＝2，所以g(－a)＝f(－a)－3＝－2，则f(－a)＝1.
2．若函数y＝f(x)的定义域是[0,2]，则函数g(x)＝eq \f(f2x,x－1)的定义域是( )
A．[0,1] B．[0,1)
C．[0,1)∪(1,4] D．(0,1)
【答案】B
【解析】根据已知可得函数g(x)＝eq \f(f2x,x－1)的定义域需满足eq \b\lc\{\rc\ (\a\vs4\al\c1(0≤2x≤2，,x≠1，))解得0≤x<1，即函数的定义域是[0,1)．
3．函数y＝lg(x＋1)－1的图象可以由函数y＝lg x的图象( )
A．上移1个单位再左移1个单位得到 B．下移1个单位再左移1个单位得到
C．上移1个单位再右移1个单位得到 D．下移1个单位再右移1个单位得到
【答案】B
【解析】令f(x)＝lg x，则有f(x＋1)－1＝lg(x＋1)－1.明显地，对于函数y＝lg(x＋1)－1的图象，可以由函数y＝lg x的图象向下移一个单位再向左移一个单位得到，故选B.
4．若aA．(a，b)和(b，c)内 B．(－∞，a)和(a，b)内
C．(b，c)和(c，＋∞)内 D．(－∞，a)和(c，＋∞)
【答案】A
【解析】∵a0，f(b)＝(b－c)(b－a)<0，f(c)＝(c－a)(c－b)>0，由函数零点存在性定理可知：在区间(a，b)，(b，c)内分别存在零点．又函数f(x)是二次函数，最多有两个零点，因此函数f(x)的两个零点分别位于区间(a，b)，(b，c)内．
5．函数f(x)＝eq \r(3＋2x－x2)的单调递增区间是( )
A．(－∞，1] B．[1，＋∞)
C．[1,3] D．[－1,1]
【答案】D
【解析】设z＝3＋2x－x2，则y＝eq \r(z)，由3＋2x－x2≥0，解得－1≤x≤3，由于z＝3＋2x－x2在[－1,1]上单调递增，在(1,3]上单调递减，又y＝eq \r(z)在定义域上单调递增，可得f(x)＝eq \r(3＋2x－x2)的单调递增区间为[－1,1]．
6．已知f(x)＝8＋2x－x2，若g(x)＝f(2－x2)，则g(x)( )
A．在区间(－1,0)内是减函数 B．在区间(0,1)内是减函数
C．在区间(－2,0)内是增函数 D．在区间(0,2)内是增函数
【答案】A
【解析】f(x)＝8＋2x－x2在(－∞，1)上单调递增，在(1，＋∞)上单调递减，
t＝2－x2在(－∞，0)上单调递增，在(0，＋∞)上单调递减，根据复合函数的单调性：
当x∈(－∞，－1)时，t∈(－∞，1)，函数g(x)单调递增；
当x∈(－1,0)时，t∈(1,2)，函数g(x)单调递减；当x∈(0,1)时，t∈(1,2)，函数g(x)单调递增；
当x∈(1，＋∞)时，t∈(－∞，1)，函数g(x)单调递减．
7．已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋1，x≥0，,－x，x<0，))则函数f(1＋2x)的图象是( )
【答案】B
【解析】由题意得，当1＋2x≥0，即x≥－eq \f(1,2)时，f(1＋2x)＝2＋2x；当1＋2x＜0，
即x＜－eq \f(1,2)时，f(1＋2x)＝－2x－1，所以f(1＋2x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(2x＋2，x≥－\f(1,2)，,－2x－1，x<－\f(1,2)，))故选B.
8．已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(lgax，0A.eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(1,6))) B.eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(1,6))) C.eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(1,4))) D．(1，＋∞)
【答案】B
【解析】 因为函数对任意x1≠x2，都有eq \f(fx1－fx2,x1－x2)<0成立，
所以函数f(x)在定义域内单调递减，所以eq \b\lc\{\rc\ (\a\vs4\al\c1(09．设函数y＝f(x)的定义域为R，则函数y＝f(x－3)与函数y＝f(1－x)的图象关于( )
A．直线y＝1对称 B．直线x＝1对称
C．直线y＝2对称 D．直线x＝2对称
【答案】D
【解析】设函数y＝f(x－3)的图象上任意一点P(x0，y0)，则y0＝f(x0－3)，且P(x0，y0)关于直线x＝2的对称点为Q(4－x0，y0)．又函数y＝f(1－x)中，当x＝4－x0时，y＝f[1－(4－x0)]＝f(x0－3)，所以Q(4－x0，y0)在y＝f(1－x)的图象上．故函数y＝f(x－3)与函数y＝f(1－x)的图象关于直线x＝2对称，故选D.
10．已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(3e－x，x≤0，,－4x＋3，x>0，))若f(a2－3)≥f(－2a)，则实数a的取值范围是( )
A．(－∞，1] B.(－∞，－3]∪[1，＋∞)
C．(－∞，1]∪[3，＋∞) D．[－3,1]
【答案】D
【解析】当x≤0时，f(x)＝3e－x单调递减；当x>0时，f(x)＝－4x＋3单调递减．
又3e0＝－4×0＋3，则函数y＝f(x)在R上连续，则函数y＝f(x)在R上单调递减．
由f(a2－3)≥f(－2a)，可得a2－3≤－2a，即a2＋2a－3≤0，
解得－3≤a≤1.因此，实数a的取值范围是[－3,1]．
11．已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(lgax，0A.eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(1,6))) B.eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(1,6))) C.eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(1,4))) D．(1，＋∞)
【答案】B
【解析】因为函数对任意x1≠x2，都有eq \f(fx1－fx2,x1－x2)<0成立，
所以函数f(x)在定义域内单调递减，所以eq \b\lc\{\rc\ (\a\vs4\al\c1(012.已知函数f(x)＝eq \f(1,ax)－ax(a>1)，则不等式f(2x2)＋f(x－1)>0的解集是( )
A．(－∞，－1)∪eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)，＋∞)) B．eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(1,2)，1)) C．eq \b\lc\(\rc\)(\a\vs4\al\c1(－∞，－\f(1,2)))∪(1，＋∞) D．eq \b\lc\(\rc\)(\a\vs4\al\c1(－1，\f(1,2)))
【答案】D
【解析】f(x)的定义域为R，且f(－x)＝ax－eq \f(1,ax)＝－f(x)，所以f(x)为奇函数．由于a>1，所以f(x)在R上递减．由f(2x2)＋f(x－1)>0，得f(2x2)>－f(x－1)＝f(1－x)，所以2x2<1－x，即2x2＋x－1＝(2x－1)(x＋1)<0，解得－113．某单位计划建一矩形场地，现有总长度为100 m的可作为围墙的材料，则场地的面积S(单位：m2)与场地的长x(单位：m)的函数关系式为____________．
【答案】S＝x(50－x)(0＜x＜50)
【解析】由于场地的长为x m，则宽为(50－x)m，由题意得S＝x(50－x)．易知x＞0,50－x＞0，所以自变量x的取值范围为0＜x＜50.故所求函数的关系式为S＝x(50－x)(0＜x＜50)．
14．已知函数f(x)＝x2－2ax＋b是定义在区间[－2b,3b－1]上的偶函数，则函数f(x)的值域为_______．
【答案】[1,5]
【解析】∵f(x)为偶函数，∴f(－x)＝f(x)，即a＝0.又f(x)的定义域为[－2b,3b－1]，
∴－2b＋3b－1＝0，解得b＝1.∴f(x)＝x2＋1，x∈[－2,2]，∴函数f(x)的值域为[1,5]．
15.已知函数f(x)满足2feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x－1,x)))＋feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x＋1,x)))＝1＋x，其中x∈R且x≠0，则函数f(x)的解析式为_______．
【答案】f(x)＝eq \f(1,3)－eq \f(1,x－1)(x≠1)．
【解析】由题意，用－x代换解析式中的x，
可得2feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x＋1,x)))＋feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x－1,x)))＝1－x，①
已知方程2feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x－1,x)))＋feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x＋1,x)))＝1＋x，②
联立①②的方程，可得feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(x＋1,x)))＝eq \f(1,3)－x.令t＝eq \f(x＋1,x)，t≠1，则x＝eq \f(1,t－1)，
所以f(t)＝eq \f(1,3)－eq \f(1,t－1)，所以f(x)＝eq \f(1,3)－eq \f(1,x－1)(x≠1)．
16.设函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(e－x＋2 019，x≤0，,2 020，x>0，))则满足f(x2－3)≤f(－2x)的x的取值范围是________．
【答案】 (－∞，－eq \r(3)]∪[1，＋∞)
【解析】因此有f(x)≥f(0)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,e)))0＋2 019＝2 020.当f(x2－3)≤f(－2x)时，
则有eq \b\lc\{\rc\ (\a\vs4\al\c1(－2x≤0，,x2－3≤0，,x2－3≥－2x))①或eq \b\lc\{\rc\ (\a\vs4\al\c1(－2x≤0，,x2－3>0)) ②或eq \b\lc\{\rc\ (\a\vs4\al\c1(－2x≥0，,x2－3≥0，)) ③
解①得，1≤x≤eq \r(3)，解②得，x>eq \r(3)，解③得，x≤－eq \r(3)，
综上所述，f(x2－3)≤f(－2x)的x的取值范围是(－∞，－eq \r(3)]∪[1，＋∞)．
17.若x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，\f(2π,3)))，则函数y＝4sin2x－12sin x－1的最大值为________，最小值为________．
【答案】B
【解析】令t＝sin x，因为x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，\f(2π,3)))，所以t∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,2)，1))，所以y＝f(t)＝4t2－12t－1.
因为该二次函数的图象开口向上，且对称轴为直线t＝eq \f(3,2)，所以当t∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(1,2)，1))时，
函数f(t)单调递减，所以当t＝－eq \f(1,2)时，ymax＝6；当t＝1时，ymin＝－9.
18．已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(1－2ax，x<1，,\f(a,x)＋4，x≥1，))且对任意的x1，x2∈R，x1≠x2时，都有eq \f(fx1－fx2,x1－x2)>0，则a的取值范围是________．
【答案】[－1,0)
【解析】由于对任意的x1，x2∈R，x1≠x2时，都有eq \f(fx1－fx2,x1－x2)>0，所以函数f(x)在R上为增函数，所以eq \b\lc\{\rc\ (\a\vs4\al\c1(1－2a>1，,a<0，,1－2a≤a＋4，))解得－1≤a<0.