2023八年级数学下册第二十二章四边形易错疑难集训一作业课件新版冀教版

这是一份2023八年级数学下册第二十二章四边形易错疑难集训一作业课件新版冀教版，共11页。
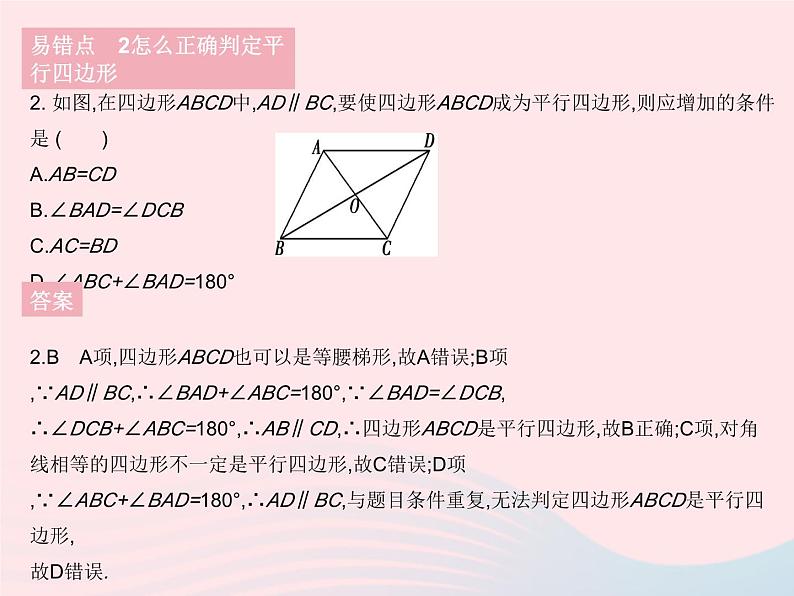
易错疑难集训（一）1. 在平行四边形ABCD中,∠A的平分线把边BC分成长度是3和4的两部分,则平行四边形ABCD的周长是 (　　)　　　　　　　　　　　　　　　　A.22 B.20C.22或20 D.18答案1.C　设∠A的平分线AE交边BC于点E.∵四边形ABCD是平行四边形,∴AB=CD,BC=AD,AD∥BC,∴∠DAE=∠BEA.∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠BEA,∴AB=BE.当BE=3,EC=4时,平行四边形ABCD的周长为2(AB+BC)=2×(3+3+4)=20.当BE=4,EC=3时,平行四边形ABCD的周长为2(AB+BC)=2×(4+4+3)=22.故平行四边形ABCD的周长为20或22.易错点1 分类讨论思想在平行四边形中的应用2. 如图,在四边形ABCD中,AD∥BC,要使四边形ABCD成为平行四边形,则应增加的条件是 (　　)A.AB=CDB.∠BAD=∠DCB C.AC=BDD.∠ABC+∠BAD=180° 答案2.B　A项,四边形ABCD也可以是等腰梯形,故A错误;B项,∵AD∥BC,∴∠BAD+∠ABC=180°,∵∠BAD=∠DCB,∴∠DCB+∠ABC=180°,∴AB∥CD,∴四边形ABCD是平行四边形,故B正确;C项,对角线相等的四边形不一定是平行四边形,故C错误;D项,∵∠ABC+∠BAD=180°,∴AD∥BC,与题目条件重复,无法判定四边形ABCD是平行四边形,故D错误.易错点　2怎么正确判定平行四边形3. 判断命题:“一组对边平行,另一组对边相等的四边形是平行四边形”是否正确,如果不正确,请举一反例.答案3.解:不正确.例如:如图,作一个平行四边形ABCD(其中∠A是锐角),以C为圆心,CB长为半径画弧,交AB的延长线于点E,连接CE,则CD∥AE,AD=CE,显然四边形AECD满足命题的条件,但它不是平行四边形.易错点　2怎么正确判定平行四边形1. [2021河北保定期末]如图,已知▱ABCO的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为 (　　)A.4 B.5 C.6 D.7 答案 疑难点　与四边形有关的动点问题2. 如图,在长方形ABCD中,AB=4 cm,BC=8 cm,动点M从点D出发,沿折线D—C—B—A—D以2 cm/s的速度运动,动点N从点D出发,沿折线D—A—B—C—D以1 cm/s的速度运动.(1)若动点M,N同时出发,经过几秒两点相遇?(2)点E在线段BC上,且BE=3 cm.若动点M,N同时出发,相遇时停止运动,则经过几秒,以点A,E,M,N为顶点的四边形是平行四边形?答案2.分析:解决动点问题的基本思路就是变“动”为“静”,要用“静”去理解“动”.在动态问题中判断平行四边形,可根据已知的一个条件,再找另一个条件,要学会在“动”中求“静”,同时要注意分类讨论,避免漏解.疑难点　与四边形有关的动点问题(1)运用方程思想,设出相遇时动点运动的时间,结合长方形的性质列出方程求解即可;(2)本小问中“动”指的是两点在长方形上运动,化“动”为“静”是根据题意及平行四边形的判定定理推出运动过程中,使以A,E,M,N为顶点的四边形成为平行四边形的状态,即根据AN=ME,列出方程求解,同时注意,分点M在点E的右侧和左侧两种情况讨论.解:(1)设t s时M,N两点相遇,根据题意,得t+2t=2×(4+8),解得t=8.答:经过8 s两点相遇.(2)由题意可知,点M不可能在线段AB或DC上.设经过a s,0