山东省滨州市惠民县2022-2023学年八年级下学期期末数学试题（含答案）

这是一份山东省滨州市惠民县2022-2023学年八年级下学期期末数学试题（含答案），共9页。试卷主要包含了答卷前，考生务必用0，第Ⅱ卷必须用0等内容，欢迎下载使用。

2022—2023学年度第二学期期末学业质量评价监测
八年级数学试题
温馨提示：
1.本试卷分第Ⅰ卷和第Ⅱ卷两部分，共6页．满分120分．考试用时120分钟．
2.答卷前，考生务必用0.5毫米黑色签字笔将自己的学校、姓名、准考证号填写在答题卡中规定的位置上．
3.第Ⅰ卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．答案不能答在试题卷上．
4.第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效．
第Ⅰ卷（选择题，共30分）
一、选择题：本大题共10个小题，满分30分，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来，每小题选对得3分，选错、不选或选出的答案超过一个均记零分．
1.已知，左边化成含有的完全平方式，其中正确的是（）
A. B.
C. D.
2.下面的说法中不正确的是（）
A.对角线互相平分的四边形是平行四边形 B.一组邻边相等的平行四边形是菱形
C.对角线互相垂直的矩形是正方形 D.对角线互相垂直的四边形是菱形
3.某校把学生的纸笔测试、实践能力、成长纪录三项成绩分别按50%、20%、30%的比例计入学期总评成绩，90分以上为优秀．甲、乙、丙三人的各项成绩如下表（单位：分），学期总评成绩优秀的是（）

纸笔测试
实践能力
成长记录
甲
90
83
95
乙
98
90
95
丙
80
88
90
A.甲 B.乙丙 C.甲乙 D.甲丙
4.将面积为的半圆与两个正方形拼接如图所示，这两个正方形面积的和为（）

A.16 B.32 C. D.64
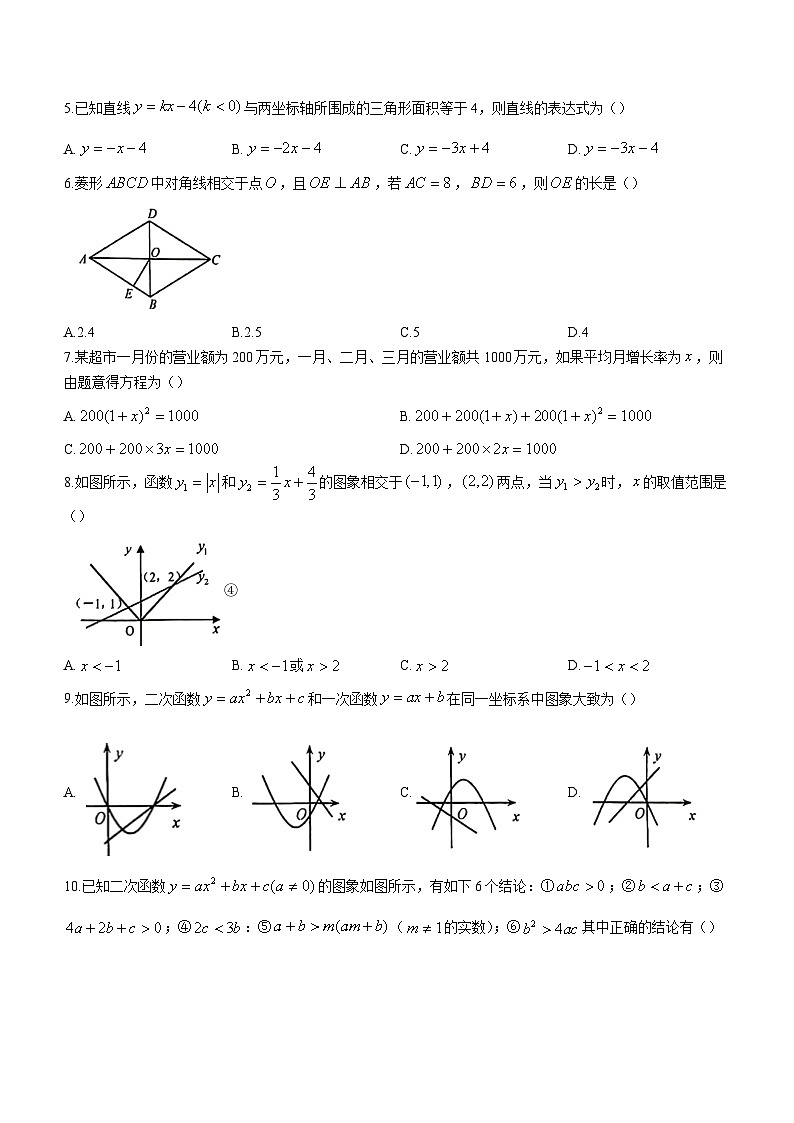
5.已知直线与两坐标轴所围成的三角形面积等于4，则直线的表达式为（）
A. B. C. D.
6.菱形中对角线相交于点，且，若，，则的长是（）

A.2.4 B.2.5 C.5 D.4
7.某超市一月份的营业额为200万元，一月、二月、三月的营业额共1000万元，如果平均月增长率为，则由题意得方程为（）
A. B.
C. D.
8.如图所示，函数和的图象相交于，两点，当时，的取值范围是（）
④
A. B.或 C. D.
9.如图所示，二次函数和一次函数在同一坐标系中图象大致为（）
A. B. C. D.
10.已知二次函数的图象如图所示，有如下6个结论：①；②；③；④：⑤（的实数）；⑥其中正确的结论有（）

A.2个 B.3个 C.4个 D.5个
第Ⅱ卷（非选择题，共90分）
二、填空题：本大题共6个小题，满分24分．
11.本数据3，6，a，4，2的平均数是4，则这个样本的方差是______．
12.如图，在中，，点、、分别为、、的中点．若，则的长为______．

13.已知，，是方程的两根，则______．
14.如图，四边形是对角线互相垂直的四边形，且，请你添加一个适当______的条件，使成为菱形（只需添加一个即可）．

15.如图，在菱形中，，与交于点，为是长线上的一点，且，连接分別交、于点、，连接，给出下列结论：①；②与全等的三角形共有5个；③四边形与四边形面积相等；④由点、、、构成的四边形是菱形．其中一定成立的是______（把所有正理命题的序号都填上）．

16.图（1）是一个横断面为拋物线形状的拱桥，当水面在时，拱顶（拱挢洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是______．

三、解答题：本大题共6个小题，满分66分．解答时请写出必要的演推过程．
17.（本题满分5分）
解方程：．
18.（本小题满分6分）
如图，是矩形的一条对角线．

（1）作的垂直平分线E，分别交，于点E、F，垂足为点O（要求用尺规作图，保留作图痕迹，不要求写作法）；
（2）若，，求的长．
19.（本题满分9分）
如图，过正方形的顶点作交的延长线于点．

（1）判断四边形的形状，并说明理由；
（2）若，求线段的长．
20.（本题满分10分）
如图1所示，在A、B两地之间有汽车站C站，客车由A地驶往C站，货车由B地经C站驶往A地．两车同时出发，匀速行驶．图2是客车、货车离C站的路程，（千米）与行驶时间x（小时）之间的函数关系图象．

（1）求A、B两地相距多少千米；
（2）求两小时后，货车离C站的路程与行驶时间x之间的函数关系式；
（3）客、货两车何时相遇？
21.（本题满分12分）
如图，利用一面墙（墙的长度不超过），用长的篱笆围成一个矩形场地，并且与墙平行的边留有宽建造一扇门方便出入（用其他材料）．设，矩形的面积为．

（1）请写出与之间的函数关系式，并写出的取值范围：
（2）怎样围才能使矩形场地的面积为？
（3）能否使所围矩形场地的面积为，若能，请算出此时矩形的长与宽，若不能，请说明理由．
22.（本题满分12分）
某建材商店代销一种建筑材料，当每吨售价为200元时，月销售量为50吨；该建材商店为提高经营利润，准备采取涨价的方式进行促销，经市场调查发现．当每吨建筑材料售价每上调10元时，月销售量就会减少2吨，每售出1吨建筑材斜共需支付厂家及其他费用100元，设每吨材料售价为x（元），该建材商店的月利润为y（元）．
（1）当每吨售价是300元时，计算此时的月钧售量：
（2）求出与的函数关系式：（写出的取值范围）
（3）该经销店要获得最大月利润，售价应定为每吨多少元？
23.（本题满分12分）
下面题目是八年级教科书中的一道题：
如图，四边形是正方形，点是边的中点，，且交正方形外角的平分线于点．求证：．（提示：取的中点，连接．）

（1）请你思考题中“提示”，这样添加辅助线的意图是什么？且完成该题的证明；
（2）若点E是边上任意一点（不与B、C重合），其他条件不变．自己画出图形，判断与是否相等，若相等，请给出证明；若不相等，请说明理由．
八年级数学期末考试答案
一、选择题：本大题共10个小题，满分30分，在每小题给出的四个选项中，只有一项是正确的，请把正确的选项选出来，每小题选对得3分，选错不选或选出的答案超过一个均记零分．
题号
1
2
3
4
5
6
7
8
9
10
选项
B
D
C
D
B
A
B
B
A
C
二、填空题：本大题共6小题，每小题4分，满分24分．
11.2 12.5 13.
14.；或；或；或；或（合情合理即可）
15.①③④ 16.
三、解答题：本大题共6个小题，满分66分．解答时请写出必要的演推过程．
17.（本题满分5分）

解：
或


注意：学生可以选择不同的解方程的方法，只要合情合理，按照完成步骤所占分量赋分即可．
18.（本小题满分6分）
解：（1）如下图：

（2）

如上图所示：连接，设，
是线段的垂直平分线，，，，
在直角三角形中，根据勾股定理可得，解得：，
即的长为5．
19.（本题满分9分）
解：（1）四边形为平行四边形．理由如下：
四边形为正方形，，
又∵点在的延长线上，，
，四边形为平行四边形．
（2）四边形为正方形，，，
，，
由（1）知，四边形为平行四边形，，
为等腰直角三角形．
，．
20.（本题满分10分）
解：（1）由函数图象可得，A，B两地相距：（千米）
（2）货车的速度是：千米/时．
设2小时后，货车离C站的路程与行驶时间x之间的函数表达式为，
根据题意得（h），（h）点的坐标为，
将点、点代入中，
解得，，．
（3）设客车离C站的路程与行驶时间x之间的函数表达式为，
根据题意得解得，，．
由得，解得．
答：客货两车在出发后小时相遇．
21.（本题满分12分）
解：（1）．．
（2）对于．．
令，即，解得：，．
墙的长度不超过45m，不合题意，应舍去．
当时，．
所以，当所围矩形的长为30m宽为25m时，能使矩形的面积为．
（3）不能．
对于．
令，即．
，．
上述方程没有实数根．
因此，不能使所围矩形场地的面积为．
22.（本题满分12分）
解：（1）当售价为300元时，月销售量为：（吨）．
（2）

（3）对于．．，函数有最大值．
当，即售价定为每吨275元时，该经销店获得最大月利润．
23.（本题满分12分）
解：（1）添加辅助线的意图是得到；
证明：如图，

作的中点，连接．
四边形是正方形，，，
，
点是的中点，点是边的中点，
，是等腰直角三角形．，
，，，
又交正方形外角的平分线于点，
，，
在和中，
，．
（2）；理由如下：
在上截取，连接，如图2所示：

四边形为正方形，，，
是等腰直角三角形，，
，，
又交正方形外角的平分线于点，
，，
，，，，，
在和中，
，．
注意：所有解答证明题，只要学生所列步骤合情合理适当赋分即可．