河北省邢台市威县2022-2023学年七年级下学期期末数学试题

这是一份河北省邢台市威县2022-2023学年七年级下学期期末数学试题，共10页。试卷主要包含了请将各题答案填写在答题卡上，若，则下列式子中不成立的是，如图，在下列条件中，能判断的是等内容，欢迎下载使用。

2022∼2023学年第二学期期末教学质量检测
七年级数学
注意事项：
1.全卷满分120分，答题时间为120分钟。
2.请将各题答案填写在答题卡上。
一、选择题（本大题共16个小题.1~10小题每题3分，11~16小题每题2分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1.下列各数中，是无理数的是（ ）
A.3.1415926 B.0 C. D.4
2.下列选项中，和是对顶角的是（ ）
A. B. C. D.
3.在平面直角坐标系中，点向左平移4个单位长度后所在的象限为（ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.用代入法解方程组时，代入正确的是（ ）
A. B.
C. D.
5.要了解某校1000名初中生的课外作业用时情况，若采用抽样调查的方法进行调查，则下列样本选择最合理的是（ ）
A.调查全体女生的作业用时
B.调查全体男生的作业用时
C.调查九年级全体学生的作业用时
D.调查七、八、九年级各100名学生的作业用时
6.若，则下列式子中不成立的是（ ）
A. B.
C. D.
7.如图，直线，将三角板按如图方式放置，直角顶点在上，若，则（ ）

A. B. C. D.
8.如图，为测量古塔的外墙底角的度数，甲、乙两人的测量方案如下：

方案一
方案二

甲：分别作，的延长线，，量出的度数，就得到的度数.

乙：作的延长线，量出的度数后可通过得到的度数.
下列判断正确的是（ ）
A.甲能得到的度数，乙不能 B.乙能得到的度数，甲不能
C.甲、乙都能得到的度数 D.甲、乙都不能得到的度数
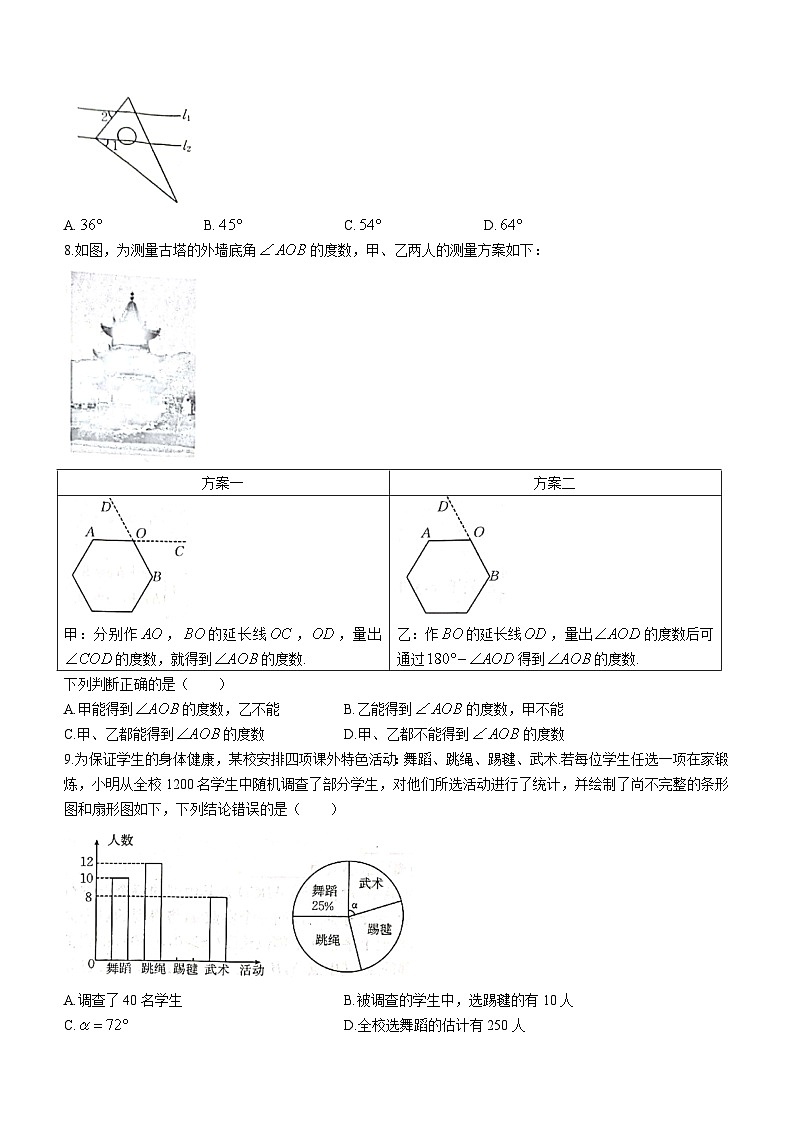
9.为保证学生的身体健康，某校安排四项课外特色活动：舞蹈、跳绳、踢毽、武术.若每位学生任选一项在家锻炼，小明从全校1200名学生中随机调查了部分学生，对他们所选活动进行了统计，并绘制了尚不完整的条形图和扇形图如下，下列结论错误的是（ ）

A.调查了40名学生 B.被调查的学生中，选踢毽的有10人
C. D.全校选舞蹈的估计有250人
10.如图，在下列条件中，能判断的是（ ）

A. B.
C. D.
11.若正方体的体积为9，则棱长的取值范围是（ ）
A.3 B. C. D.
12.某班45名学生的成绩被分为5组，第组的频数分别为12，11，9，4，则第5组的频率是（ ）
A.0.1 B.0.2 C.0.3 D.0.4
13.关于的一元一次不等式组的解集为（ ）
A. B. C. D.
14.如图，，，，则等于（ ）

A. B. C. D.
15.已知是关于，的二元一次方程组的解，则的值为（ ）
A.2 B. C. D.0
16.如图，，点到直线的距离为3，若在射线上只存在一个点，记的长度为，则的值可以是（ ）

A.7 B.2 C.5 D.6
二、填空题（本大题共3个小题，每小题3分，共9分.其中18小题第一空2分，第二空1分；19小题每空1分）
17.如果某个数的一个平方根是，那么这个数的算术平方根是______.
18.若第二象限内的点到轴的距离为3，到轴的距离为2，点.
（1）点的坐标为______.
（2）点与点的距离的最小值为______.
19.如图，在平面直角坐标系中，对正方形及其内部的每个点进行如下操作：把每个点的横、纵坐标都乘以同一个实数，将得到的点先向右平移个单位长度，再向上平移个单位长度，得到正方形及其内部的点，其中点，的对应点分别为，.已知正方形内部的一点经过上述操作后得到的对应点与点重合.

（1）______，______.
（2）点的坐标是______.
三、解答题（本大题共7个小题，共69分.解答应写出文字说明、证明过程或演算步骤）
20.（本小题满分9分）
（1）计算：.
（2）解方程组：.
21.（本小题满分9分）
为丰富学生课余生活，某校准备开设.剪纸；.篮球；.绘画；.足球；.书法五种社团活动课.为了解同学们的喜爱情况，学校随机调查了本校部分同学（每人只能选择一种社团活动课），然后利用所得数据绘制成如下两幅不完整的统计图表：

根据以上图表，解答下列问题：
（1）______，补全条形统计图.
（2）求扇形统计图中扇形的圆心角的度数.
（3）若该校有2000名学生，请估计全校有多少名学生选择足球社团.
22.（本小题满分9分）
如图，在平面直角坐标内有三角形，其中，，，在坐标平面内放置一透明胶片，并在胶片上描画出点.平移该胶片使点落在点处.
（1）若点，点都与点做同样的平移运动，点，平移后的对应点分别为点，，写出点，的坐标，______，______，并在坐标平面内画出三角形.
（2）求三角形的面积.

23.（本小题满分10分）
如图，，.
（1）判断与的位置关系，并说明理由.
（2）若平分，平分，且，求的度数.

24.（本小题满分10分）
如图，在一条不完整的数轴上从左到右有点，，，其中，.设点，，在数轴上所对应数的和是.
（1）若的值不大于11，求点表示的数的最大值.
（2）若原点在图中数轴上点的右边个单位长度，且不小于，求的最大值.

25.（本小题满分10分）
某文具经销商计划购进一批签字笔，已知供货商有，，三种不同价格的签字笔，进价分别是种签字笔每箱1500元，种签字笔每箱2000元，种签字笔每箱2500元.
（1）求花费50000元购进24箱签字笔的平均价格.
（2）若经销商同时购进两种不同型号的签字笔24箱，刚好用去50000元，请你设计采购方案.
26.（本小题满分12分）
已知直线，直线分别与，交于点，.
（1）如图1，是，之间的一点，连接，.
①若平分，平分，求的度数.
②求证：.
（2）如图2，平分，过点分别作射线和交于点，，若，猜想和之间的数量关系，并证明.

图1 图2


2022~2023学年第二学期期末教学质量检测
七年级数学参考答案
1.C 2.D 3.C 4.A 5.D 6.D 7.C 8.C 9.D 10. A 11.C 12.B 13.D 14. A 15.A 16.A
17.5 18.（1）（2）4
19.（1）；2 （2）
提示：点对应点，点对应点，由横坐标的变化可列方程组，解得，.
由纵坐标的变化列方程，解得.
设点，那么，解得.
，解得，
所以点的坐标是.
20.解：（1）原式

.
（2）由②，得③，
把③代入①，得，
解得
把代入③，得
∴原方程组的解为.
21.解：（1）8.
补全条形统计图如下：

（2），
∴扇形统计图中扇形的圆心角的度数为.
6分
（3）（名），
∴估计全校有640名学生选择足球社团.
22.解：（1）；.
三角形如图所示

（2）.
23.解：（1）.
理由：∵，∴.
∵，
∴
∴.
（2）∵，
∴.
∵平分，
∴，
∴.
∵平分，
∴.
24.解：（1）∵点表示的数为，
∴点表示的数为，点表示的数为，
由题可得，
解得，
∴的最大值是2.
（2）∵原点在图中数轴上点的右边个单位长度，
∴点表示为，点表示为，点表示为
由题可得
解得分
∴的最大值为6.
25.解：（1）（元）.
答：购进24箱签字笔的平均价格为元.
（2）∵购进24箱签字笔的平均价格为（元），
∴必须购进种签字笔.
若设购进种签字笔支，种签字笔支，
根据题意，得，
解得.
若设购进种签字笔支，种签字笔支，
根据题意，得，
解得.
综上所述，若经销商同时购进两种不同型号的签字笔共有两种方案可行，即种签字笔10箱，种签字笔14箱或种签字笔20箱，种签字笔4箱.
26.解：（1）①∵，
∴.
∵平分，平分，
∴，
∴.
②如图1，过点作.
∵，
∴.
又∵，
∴，
∴.
又，
∴

图1
（2）.
证明：如图2，过点作.
∵，∴，∴.
由（1）可得，.
∵平分，
∴.
∵，

图2
∴.
∵，
∴.
∵，
∴，
∴.