





八年级数学上册作期末复习-坐标变化与一次函数课件PPT
展开1. (1)将直线y=2x+3向下平移2个单位得到的直线表达式是 .(2)将直线y=2x+3先向左平移3个单位,再向下平移2个单位得到的直线表达式是 .
一、 一次函数图象的对称
2. (1)点P(-2,0)关于y轴对称的点的坐标是 ;直线y=2x+4关于y轴对称的直线的表达式是 .(2)点B(0,4)关于x轴对称的点的坐标是 ;直线y=2x+4关于x轴对称的直线的表达式是 .
(3)直线y=kx+b关于y轴对称的直线的表达式是 .(4)直线y=kx+b关于x轴对称的直线的表达式是 .
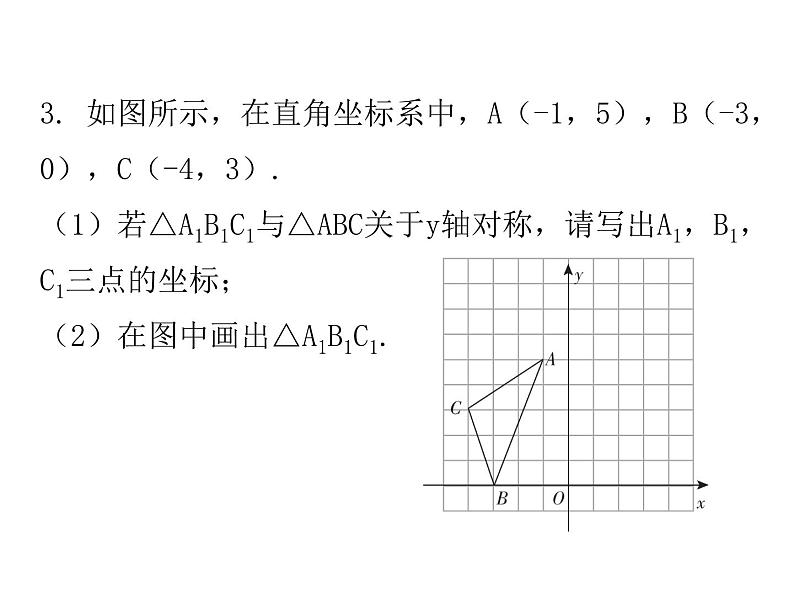
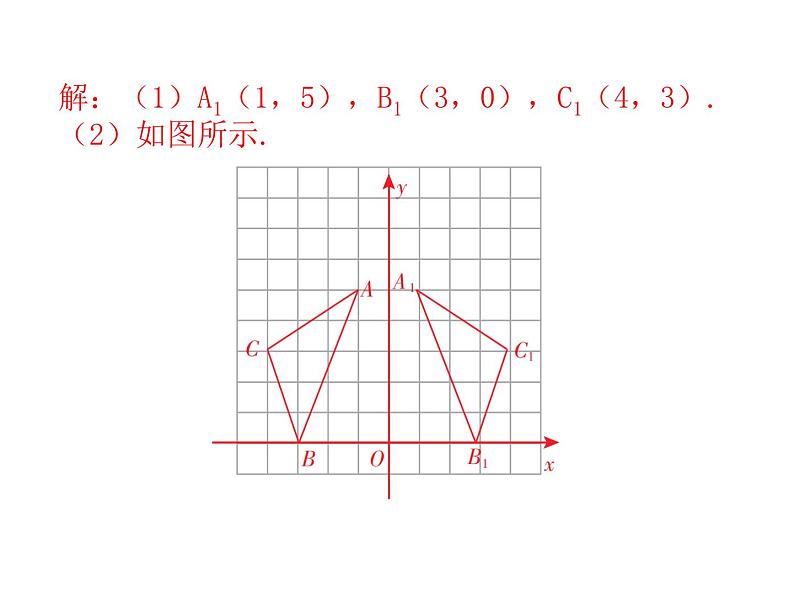
3. 如图所示,在直角坐标系中,A(-1,5),B(-3,0),C(-4,3).(1)若△A1B1C1与△ABC关于y轴对称,请写出A1,B1,C1三点的坐标;(2)在图中画出△A1B1C1.
4. 已知一次函数y=(m-3)x+2m+4的图象经过点M(1,1).(1)求它的函数表达式;(2)求这条直线与两坐标轴所围成的三角形的面积.
5. 如图,已知直线l1∶y=2x+3和直线l2∶y=-x+5,直线l1、l2分别交x轴于B,C两点,l1、l2相交于点A. (1)求A,B,C三点坐标;(2)求△ABC的面积.
6. 如图,已知直线l1经过点A(-1,0)与点B(2,3),另一条直线l2,经过点B,且与x轴相交于点P(m,0).(1)求直线l1的表达式;(2)若△APB的面积为3,求m的值.
解:(1)设直线l1的表达式为y=kx+b,∵直线l1经过点A(-1,0)与点B(2,3),∴k+b=0,2k+b=3,则k=1,b=1.∴直线l1的表达式为y=x+1.
7. 如图,已知正比例函数y= x与一次函数y=-x+7的图象交于点A.
8.矩形ABCD在如图所示的平面直角坐标系中,点A的坐标为(0,3),BC=2AB,直线经过点B,交AD边于点P1,此时直线l的函数表达式是y=2x+1.
解:(1)∵直线y=2x+1经过y轴上的点B,∴B(0,1).∵A的坐标为(0,3),∴AB=2,BC=2AB=4,P1(1,3),AP1=1.
(1)求BC,AP1的长;
(2)沿y轴负方向平移直线l,分别交AD,BC边于点P,E.①当四边形BEPP1是菱形时,求平移的距离;②设AP=m,当直线l把矩形ABCD分成两部分的面积之比为3∶5时,求m的值.
9. 如图,直线y=x+1交x轴于点A,交y轴于点C,OB=3OA ,点M在直线AC上,AC=CM.(1)求直线BM的表达式;(2)如图,点N在MB的延长线上,BN=AC,连CN交x轴于点P,求点P的坐标.
解:(1)由题意可知,A点坐标(-1,0),点C坐标(0,1)∵OB=3OA,∴点B坐标(3,0).∵M在AC上,且AC=CM,M在第一象限,∴点M坐标(1,2) .设BM表达式为y=kx+b, ∴0=3k+b,2=k+b.解得k=-1,b=3. ∴ BM表达式为y=-x+3.
10. 如图1,已知直线AB分别交x轴,y轴于A(4,0),B两点,C(-4,a)为直线y=-x与AB的公共点.
(2)已知动点M在直线y=x+6上,是否存在点M使得S△OMB=S△OMA?若存在,求出点M的坐标,若不存在,说明理由;
(3)如图2,已知,P是x轴正半轴上动点,Q是y轴正半轴上的动点,Q在点E上方,OP=BQ,QH是∠OQP的平分线,交直线CO于点H,求OB、PQ、OH之间的数量关系.
设点H(t,-t),P(a,0),QH与x轴的交点为M,如图所示,作HN⊥y轴于点N,HF⊥PQ于点F,HM⊥x轴于点M.则HN=HM=HF,△QHN≌△QHF,易证PF=MP=a-t.
初中数学北师大版八年级上册3 轴对称与坐标变化课前预习ppt课件: 这是一份初中数学北师大版八年级上册3 轴对称与坐标变化课前预习ppt课件,共18页。
八年级数学上册作期末复习-作图课件PPT: 这是一份八年级数学上册作期末复习-作图课件PPT,共45页。PPT课件主要包含了平行线的作图等内容,欢迎下载使用。
初中数学北师大版八年级上册3 轴对称与坐标变化图文ppt课件: 这是一份初中数学北师大版八年级上册3 轴对称与坐标变化图文ppt课件,共30页。PPT课件主要包含了学习目标1分钟,自学指导2分钟,自学检测12分钟,-xy,x-y,-x-y,当堂训练18分钟,课堂检测,本节课你学到了什么,感悟与反思等内容,欢迎下载使用。












