





还剩27页未读,
继续阅读
第四章一次函数单元复习-(北师大)课件PPT
展开
这是一份第四章一次函数单元复习-(北师大)课件PPT,共35页。
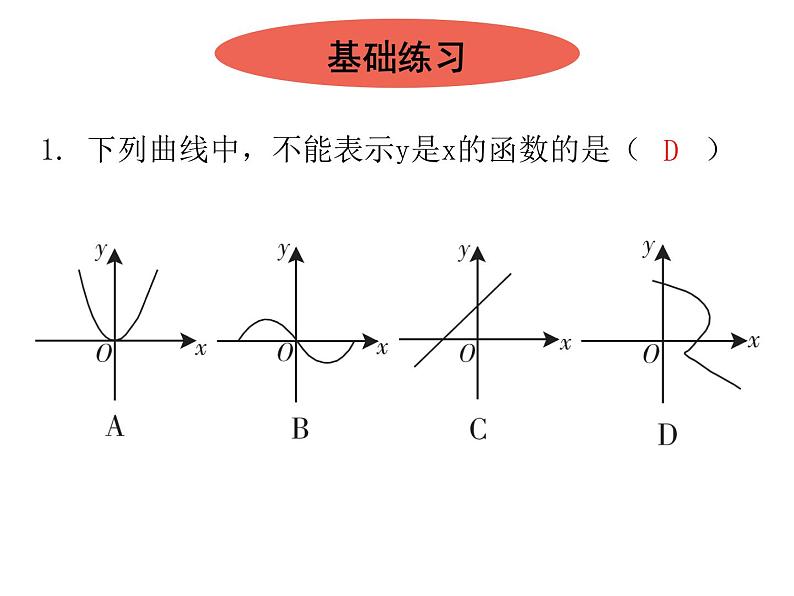
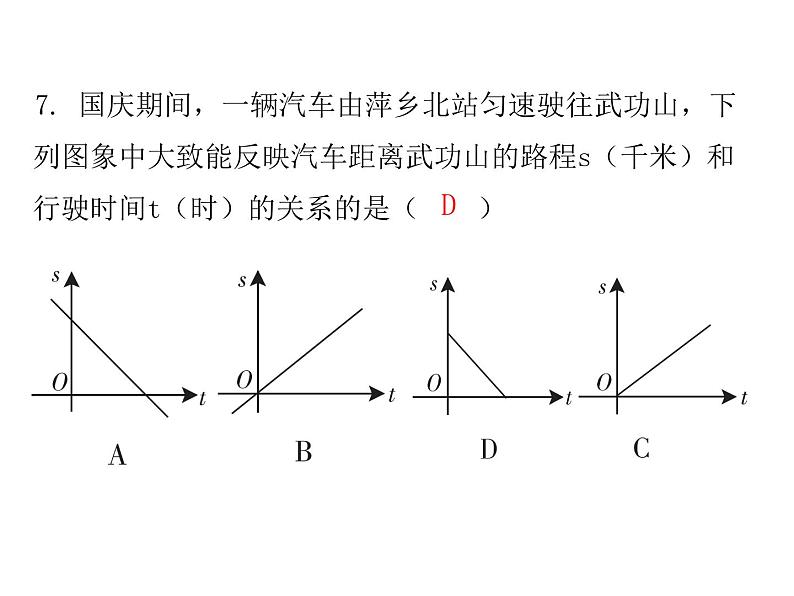
1. 下列曲线中,不能表示y是x的函数的是( )基础练习D2. 嘉嘉买了6支笔花了9元钱,琪琪买了同样售价的x支笔,还买了单价为5元的三角尺两副,用y(元)表示琪琪花的总钱数,那么y与x之间的关系式应该是( )A. y=1.5x+10 B. y=5x+10 C. y=1.5x+5 D. y=5x+5A3. 下列函数中,自变量x的取值范围是x≥2的是( )C4. 当x=2时,函数y=- x2+1的值是( )A. -2 B. -1 C. 2 D. 3B5. ①y=kx;②y= x;③y=x2-(x-1)x;④y=x2+1;⑤y=22-x,一定是一次函数的个数有( )A. 2个 B. 3个 C. 4个 D. 5个B6. 若y=x+2-b是正比例函数,则b的值是( )A. 0 B. -2 C. 2 D. -0.5C7. 国庆期间,一辆汽车由萍乡北站匀速驶往武功山,下列图象中大致能反映汽车距离武功山的路程s(千米)和行驶时间t(时)的关系的是( )D8. 能表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数且m≠0)的图象的是( )C9. 甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息分析,下列说法正确的是( )A. 甲队开挖到30 m时,用了2 h B. 乙队在0≤x≤6的时段,y与x之间的关系式y=5x+20C. 当两队所挖长度之差为5 m时,x为3和5 D. x为4时,甲、乙两队所挖的河渠长度相等D10. 如图,在平面直角坐标系中,已知一次函数y=- x+6与x轴,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )A. (0,3) B. (0, ) C. (0, ) D. (0, )D11. 请写出一个图象从左至右上升且经过点(-1,2)的一次函数: .y=x+3(答案不唯一) 12. 已知直线y=kx+b,若k+b=-5,kb=6,那么该直线不经过第 象限.113. 如果一次函数y=kx+b的自变量x的取值范围是1≤x≤6,相应的函数值的取值范围是-10≤y≤5,那么k+b的值是 .-10或514. 如图,直线y=- x+4与x轴,y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .(7,3)15. 已知y+4与x成正比例,且当x=3时,y=2.(1)求y关于x的函数表达式;(2)在图中画出(1)中所求函数的图象并求出图象与两坐标轴围成的图形的面积.综合练习解:(1)∵y+4与x成正比例,∴可设y+4=kx. ∵当x=3时,y=2,∴2+4=3k. ∴k=2. ∴y+4=2x. ∴y关于x的函数表达式为y=2x-4.16. 如图,一次函数的图象分别与x轴,y轴交于点A(2,0),B(0,4).(1)求函数的表达式.(2)在该一次函数图象上有一点P到x轴的距离为6,求点P的坐标.(2)点P为一次函数图象上一点,设P(x,-2x+4).∵有一点P到x轴的距离为6,∴分两种情况讨论.①-2x+4=6,解得x=-1.此时P(-1,6).②-2x+4=-6,解得x=5.此时P(5,-6).故点P的坐标(-1,6)或(5,-6).17. 某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7 200元.(1)根据图象,求y与x之间的函数关系式;(2)求甲、乙两种品牌的文具盒进货单价;∵y=-x+300,∴当x=120时,y=180. 设甲品牌进货单价是a元,则乙品牌的进货单价是2a元,由题意,得120a+180×2a=7 200.解得a=15.∴乙品牌的进货单价是30元.答:甲、乙两种品牌的文具盒进货单价分别为15元,30元.(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6 300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1 795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?方案1:甲品牌进货180个,则乙品牌的进货120个;方案2:甲品牌进货181个,则乙品牌的进货119个;设两种品牌的文具盒全部售出后获得的利润为W元,由题意,得W=4m+9(-m+300)=-5m+2 700. ∵k=-5<0,∴W随m的增大而减小,∴当m=180时,W最大=1 800元.18. 如图,在直角坐标系中,已知点A(-3,0)和点B(1,0),以AB为边在x轴上方作正方形ABCD,点P是x轴负半轴上一点,连接DP,过点P作DP的垂线与y轴负半轴交于点E,PD=PE,连接DE. (1)求点D的坐标;解:(1)由四边形ABCD是正方形,得AD=AB=1-(-3)=4,AO=3,点D坐标为(-3,4).(2)求直线DE的表达式;(2)求直线DE的表达式;(3)求△ADF的周长.
1. 下列曲线中,不能表示y是x的函数的是( )基础练习D2. 嘉嘉买了6支笔花了9元钱,琪琪买了同样售价的x支笔,还买了单价为5元的三角尺两副,用y(元)表示琪琪花的总钱数,那么y与x之间的关系式应该是( )A. y=1.5x+10 B. y=5x+10 C. y=1.5x+5 D. y=5x+5A3. 下列函数中,自变量x的取值范围是x≥2的是( )C4. 当x=2时,函数y=- x2+1的值是( )A. -2 B. -1 C. 2 D. 3B5. ①y=kx;②y= x;③y=x2-(x-1)x;④y=x2+1;⑤y=22-x,一定是一次函数的个数有( )A. 2个 B. 3个 C. 4个 D. 5个B6. 若y=x+2-b是正比例函数,则b的值是( )A. 0 B. -2 C. 2 D. -0.5C7. 国庆期间,一辆汽车由萍乡北站匀速驶往武功山,下列图象中大致能反映汽车距离武功山的路程s(千米)和行驶时间t(时)的关系的是( )D8. 能表示一次函数y=mx+n与正比例函数y=mnx(m,n是常数且m≠0)的图象的是( )C9. 甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息分析,下列说法正确的是( )A. 甲队开挖到30 m时,用了2 h B. 乙队在0≤x≤6的时段,y与x之间的关系式y=5x+20C. 当两队所挖长度之差为5 m时,x为3和5 D. x为4时,甲、乙两队所挖的河渠长度相等D10. 如图,在平面直角坐标系中,已知一次函数y=- x+6与x轴,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )A. (0,3) B. (0, ) C. (0, ) D. (0, )D11. 请写出一个图象从左至右上升且经过点(-1,2)的一次函数: .y=x+3(答案不唯一) 12. 已知直线y=kx+b,若k+b=-5,kb=6,那么该直线不经过第 象限.113. 如果一次函数y=kx+b的自变量x的取值范围是1≤x≤6,相应的函数值的取值范围是-10≤y≤5,那么k+b的值是 .-10或514. 如图,直线y=- x+4与x轴,y轴分别交于A,B两点,把△AOB绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .(7,3)15. 已知y+4与x成正比例,且当x=3时,y=2.(1)求y关于x的函数表达式;(2)在图中画出(1)中所求函数的图象并求出图象与两坐标轴围成的图形的面积.综合练习解:(1)∵y+4与x成正比例,∴可设y+4=kx. ∵当x=3时,y=2,∴2+4=3k. ∴k=2. ∴y+4=2x. ∴y关于x的函数表达式为y=2x-4.16. 如图,一次函数的图象分别与x轴,y轴交于点A(2,0),B(0,4).(1)求函数的表达式.(2)在该一次函数图象上有一点P到x轴的距离为6,求点P的坐标.(2)点P为一次函数图象上一点,设P(x,-2x+4).∵有一点P到x轴的距离为6,∴分两种情况讨论.①-2x+4=6,解得x=-1.此时P(-1,6).②-2x+4=-6,解得x=5.此时P(5,-6).故点P的坐标(-1,6)或(5,-6).17. 某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7 200元.(1)根据图象,求y与x之间的函数关系式;(2)求甲、乙两种品牌的文具盒进货单价;∵y=-x+300,∴当x=120时,y=180. 设甲品牌进货单价是a元,则乙品牌的进货单价是2a元,由题意,得120a+180×2a=7 200.解得a=15.∴乙品牌的进货单价是30元.答:甲、乙两种品牌的文具盒进货单价分别为15元,30元.(3)若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6 300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1 795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?方案1:甲品牌进货180个,则乙品牌的进货120个;方案2:甲品牌进货181个,则乙品牌的进货119个;设两种品牌的文具盒全部售出后获得的利润为W元,由题意,得W=4m+9(-m+300)=-5m+2 700. ∵k=-5<0,∴W随m的增大而减小,∴当m=180时,W最大=1 800元.18. 如图,在直角坐标系中,已知点A(-3,0)和点B(1,0),以AB为边在x轴上方作正方形ABCD,点P是x轴负半轴上一点,连接DP,过点P作DP的垂线与y轴负半轴交于点E,PD=PE,连接DE. (1)求点D的坐标;解:(1)由四边形ABCD是正方形,得AD=AB=1-(-3)=4,AO=3,点D坐标为(-3,4).(2)求直线DE的表达式;(2)求直线DE的表达式;(3)求△ADF的周长.
相关资料
更多









