2023年江苏省连云港市赣榆区中考数学二模试卷（含解析）

这是一份2023年江苏省连云港市赣榆区中考数学二模试卷（含解析），共24页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。

2023年江苏省连云港市赣榆区中考数学二模试卷
一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）
1. 化简( 3)2的结果是(    )
A. −3 B. 3 C. ±3 D. 9
2. 在中国园林建筑中，洞窗是最生动的眼睛，主要以漏空图案填心为主，故也称镂空花窗.花窗图案丰富多样，以各种植物，动物，字体，几何图案和其他图案为基础，相互交错形成多种吉祥图案.则下列填心的图案中不是轴对称图形的是(    )
A. B. C. D.
3. 2023年的“五一”假日期间，连云港市迎来疫情后首个旅游高峰.据统计，连云港全市共接游客365.3万人次，实现旅游总收入5114000000元，其中“5114000000”用科学记数法表示为(    )
A. 5.114×108 B. 51.14×108 C. 5.114×109 D. 5.114×107
4. 已知正多边形的一个外角等于60°，则该正多边形的边数为(    )
A. 3 B. 4 C. 5 D. 6
5. 小红在“养成阅读习惯，快乐阅读，健康成长”读书大赛活动中，随机调查了本校初二年级20名同学，在近5个月内每人阅读课外书的数量，数据如下表所示：
人数
3
4
8
5
课外书数量(本)
12
13
15
18
则阅读课外书数量的中位数和众数分别是(    )
A. 35，15 B. 14，15 C. 13，18 D. 15，15
6. 如图，将一副三角板叠放在一起，使直角的顶点重合于点O，AB//OC，DC与OB交于点E，则∠DEO的度数为(    )
A. 85°
B. 70°
C. 75°
D. 60°
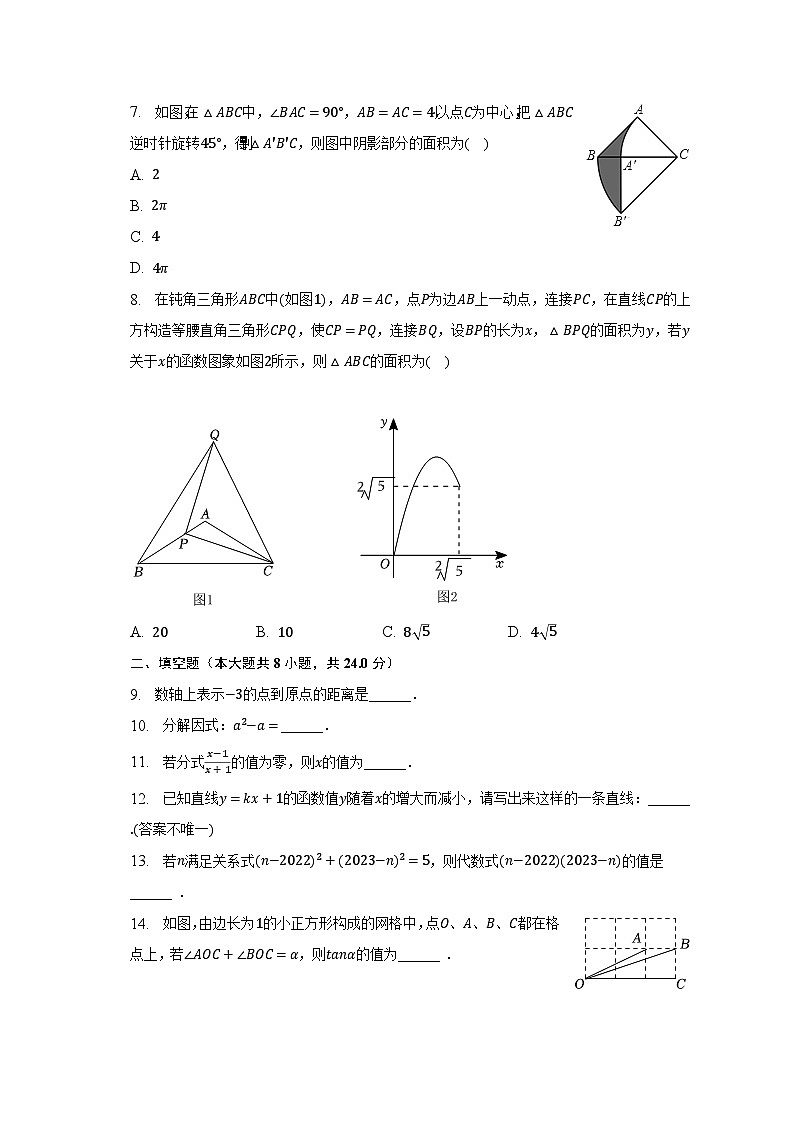
7. 如图，在△ABC中，∠BAC=90°，AB=AC=4，以点C为中心，把△ABC逆时针旋转45°，得到△A′B′C，则图中阴影部分的面积为(    )
A. 2
B. 2π
C. 4
D. 4π
8. 在钝角三角形ABC中(如图1)，AB=AC，点P为边AB上一动点，连接PC，在直线CP的上方构造等腰直角三角形CPQ，使CP=PQ，连接BQ，设BP的长为x，△BPQ的面积为y，若y关于x的函数图象如图2所示，则△ABC的面积为(    )


A. 20 B. 10 C. 8 5 D. 4 5
二、填空题（本大题共8小题，共24.0分）
9. 数轴上表示−3的点到原点的距离是______．
10. 分解因式：a2−a=______．
11. 若分式x−1x+1的值为零，则x的值为______．
12. 已知直线y=kx+1的函数值y随着x的增大而减小，请写出来这样的一条直线：______ .(答案不唯一)
13. 若n满足关系式(n−2022)2+(2023−n)2=5，则代数式(n−2022)(2023−n)的值是______ ．
14. 如图，由边长为1的小正方形构成的网格中，点O、A、B、C都在格点上，若∠AOC+∠BOC=α，则tanα的值为______ ．


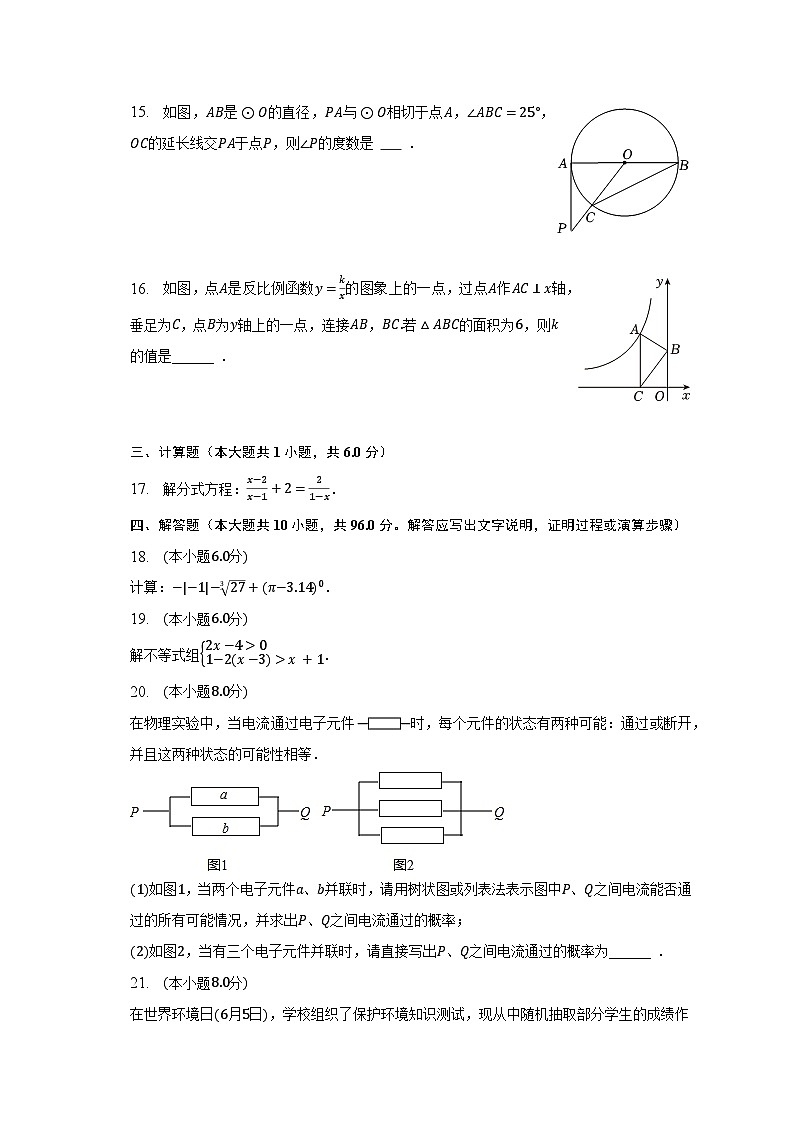
15. 如图，AB是⊙O的直径，PA与⊙O相切于点A，∠ABC=25°，OC的延长线交PA于点P，则∠P的度数是        ．


16. 如图，点A是反比例函数y=kx的图象上的一点，过点A作AC⊥x轴，垂足为C，点B为y轴上的一点，连接AB，BC.若△ABC的面积为6，则k的值是______ ．


三、计算题（本大题共1小题，共6.0分）
17. 解分式方程：x−2x−1+2=21−x．
四、解答题（本大题共10小题，共96.0分。解答应写出文字说明，证明过程或演算步骤）
18. (本小题6.0分)
计算：−|−1|−327+(π−3.14)0．
19. (本小题6.0分)
解不等式组2x−4>01−2(x−3)>x+1．
20. (本小题8.0分)
在物理实验中，当电流通过电子元件时，每个元件的状态有两种可能：通过或断开，并且这两种状态的可能性相等．

(1)如图1，当两个电子元件a、b并联时，请用树状图或列表法表示图中P、Q之间电流能否通过的所有可能情况，并求出P、Q之间电流通过的概率；
(2)如图2，当有三个电子元件并联时，请直接写出P、Q之间电流通过的概率为______ ．
21. (本小题8.0分)
在世界环境日(6月5日)，学校组织了保护环境知识测试，现从中随机抽取部分学生的成绩作为样本，按“优秀”“良好”“合格”“不合格”四个等级进行统计，绘制了如下尚不完整的统计图表．
测试成绩统计表
等级
频数(人数)
频率
优秀
30
a
良好
b
0.45
合格
24
0.20
不合格
12
0.10
合计
c
1
根据统计图表提供的信息，解答下列问题：
(1)表中a= ______ ，b= ______ ，c= ______
(2)补全条形统计图；
(3)若该校有800名学生参加了本次测试，估计测试成绩等级在良好以上(包括良好)的学生约有多少人？

22. (本小题10.0分)
如图，点B，E，C，F在一条直线上，AC与DE相交于点O，AB=DE，AB//DE，AC//DF．
(1)求证：△ABC≌△DEF；
(2)若∠B=55°，∠EOC=80°，求∠F的度数．

23. (本小题10.0分)
在学校开展“劳动创造美好生活”主题系列活动中，八年级(1)班负责校园某绿化角的设计、种植与养护．同学们约定每人养护一盆绿植，计划购买绿萝和吊兰两种绿植共46盆，且绿萝盆数不少于吊兰盆数的2倍．已知绿萝每盆9元，吊兰每盆6元．
(1)采购组计划将预算经费390元全部用于购买绿萝和吊兰，问可购买绿萝和吊兰各多少盆？
(2)规划组认为有比390元更省钱的购买方案，请求出购买两种绿植总费用的最小值．
24. (本小题10.0分)
动感单车是一种新型的运动器械．图①是一辆动感单车的实物图，图②是其侧面示意图．△BCD为主车架，AB为调节管，点A，B，C在同一直线上．已知BC长为70cm，∠BCD的度数为58°.当AB长度调至34cm时，求点A到CD的距离AE的长度(结果精确到1cm).(参考数据：sin58°≈0.85，cos58°≈0.53，tan58°≈1.60)

25. (本小题12.0分)
在平面直角坐标系中，已知一次函数y1=k1x+b与坐标轴分别交于A(5,0)，B(0,52)两点，且与反比例函数y2=k2x的图象在第一象限内交于P，Q两点，连接OP，△OAP的面积为54．
(1)求一次函数与反比例函数的表达式；
(2)当y2>y1时，请你直接写出x的取值范围；
(3)若C为线段OA上的一个动点，当PC+QC最小时，求△PQC的面积．

26. (本小题12.0分)
如图1，在矩形ABCD中，点E是边BC的中点，ABBE=k(k>1)，连接AE，过点E作EG⊥AE，并与矩形的外角∠DCF的平分线CG交于点G．

(1)求AEEG的值(用含k的代数式表示)；
(2)连接AG交CD于点H，连接EH，若∠AHE=90°，求k的值；
(3)如图2，当k与题(2)取相同值时，P为边CD上一点，连接AP、PG，当PG= 5，∠PAE=45°时，求BC的长．
27. (本小题14.0分)
在平面直角坐标系中，抛物线L1：y=ax2+x+c(a>0)与x轴交于A(−2,0)、B(1,0)两点，与y轴交于点C．
(1)求抛物线L1对应的函数表达式；
(2)如图1，点D为直线AC下方抛物线上的一动点，DM⊥AC于点M，DN//y轴交AC于点N，求线段DM的最大值和此时点D的坐标；
(3)如图2，将抛物线L1：y=ax2+x+c(a>0)沿着x轴向左平移后得到抛物线L2，若点P是抛物线L1与L2在x轴下方的交点且tan∠ACP=13，求抛物线L2对应的函数表达式．

答案和解析

1.【答案】B 
【解析】
【分析】
本题考查了二次根式的乘法，解答本题的关键是掌握二次根式的乘法法则： a⋅ b= ab．
按照二次根式的乘法法则求解．
【解答】
解：( 3)2= 3· 3= 9=3．
故选B．  
2.【答案】D 
【解析】解：A、是轴对称图形，不符合题意，
B、是轴对称图形，不符合题意，
C、是轴对称图形，不符合题意，
D、不是轴对称图形，符合题意，
故选：D．
根据轴对称图形的概念逐项判定即可．
本题考查了轴对称图形的定义，正确理解定义是解题的关键．

3.【答案】C 
【解析】解：5114000000=5.114×109．
故选：C．
科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数，当原数绝对值<1时，n是负整数．
此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．

4.【答案】D 
【解析】
解：360°÷60°=6．
故该正多边形的边数为6．
故选：D．
【分析】此题主要考查了多边形内角与外角，关键是掌握多边形外角和为360°．
利用外角和360°÷外角的度数即可得到边数．  
5.【答案】D 
【解析】解：中位数为第10个和第11个的平均数15+152=15，众数为15．
故选：D．
利用中位数，众数的定义即可解决问题．
本题考查了中位数和众数，解答本题的关键是掌握中位数和众数的概念．

6.【答案】C 
【解析】解：∵AB//OC，∠A=60°，
∴∠A+∠AOC=180°，
∴∠AOC=120°，
∴∠BOC=120°−90°=30°，
∴∠DEO=∠C+∠BOC=45°+30°=75°；
故选：C．
由平行线的性质求出∠AOC=120°，再求出∠BOC=30°，然后根据三角形的外角性质即可得出结论．
本题主要考查了平行线的性质、三角形的外角性质；熟练掌握平行线的性质和三角形的外角性质是解决问题的关键．

7.【答案】B 
【解析】解：∵在△ABC中，∠BAC=90°，AB=AC=4，
∴BC= AB2+AC2=4 2，∠ACB=∠A′CB′=45°，
∴阴影部分的面积=45π⋅(4 2)2360−12×4×4+12×4×4−45π⋅42360=2π．
故选B．
根据阴影部分的面积列式，代入数值解答即可．
本题考查了扇形面积公式的应用，以及旋转的基本性质．

8.【答案】D 
【解析】解：由图2可得，当x=2 5，y=2 5，点P运动到点A的位置，
过点Q、C分别作BA的垂线，垂足为D、E，如图：


∵AB=AC=PQ=2 5，S△BPQ=12BP⋅DQ=2 5，三角形CPQ是等腰直角三角形，
∴PQ=PC，即AC=AQ=2 5，
∴QD=2
∴AD= AQ2−QD2= 20−4=4，
∵∠QPC=90°，
∴∠CAE=∠AQD，
∴△ACE≌△QAD(AAS)，
∴CE=AD=4，
∴S△ABC=12AB⋅EC=12×2 5×4=4 5．
故选：D．
根据图2可得，当x=2 5，y=2 5，点P运动到点A的位置，过点Q、C分别作BA的垂线，垂足为D、E，然后根据三角形的面积求出QD，从而得出AD，再根据三角形CPQ是等腰直角三角形证明△ACE≌△QAD得出CE=AD=4，然后由三角形的面积公式求出△ABC的面积．
本题考查动点问题的函数图象，关键是根据图中信息，找到点P相应的位置．

9.【答案】3 
【解析】
【分析】
本题考查数轴，表示−3的点与原点的距离是−3的绝对值．据此作答即可．
【解答】
解：在数轴上表示−3的点与原点的距离是|−3|=3．
故答案为：3．  
10.【答案】a(a−1) 
【解析】解：a2−a=a(a−1)．
这个多项式含有公因式a，分解因式时应先提取公因式．
本题考查了提公因式法分解因式，比较简单，注意不要漏项．

11.【答案】1 
【解析】解：x−1x+1=0，
则x−1=0，x+1≠0，
解得x=1．
故若分式x−1x+1的值为零，则x的值为1．
故答案为：1．
分式的值为0的条件是分子为0，分母不能为0，据此可以解答本题．
本题考查分式的值为0的条件，注意分子为0，分母不能为0这一条件．

12.【答案】y=−x+1 
【解析】解：∵直线y=kx+1的函数值y随着x的增大而减小，
∴k<0，
∴符合这样要求的直线可以是y=−x+1．
故答案为：y=−x+1．
根据一次函数的性质当一次函数y=kx+b的k小于0时，y随着x的增大而减小，所以只要选取一个k小于0的值即可．
此题主要是考查了一次函数的性质，对于一次函数y=kx+b，当k大于0时，y随着x的增大而增大，当k小于0时，y随着x的增大而减小．

13.【答案】−2 
【解析】解：设n−2022=a，2023−n=b，
则a+b=1，a2+b2=5，
∴(n−2022)(2023−n)=ab=(a+b)2−(a2+b2)2=12−52=−2，
故答案为：−2．
设n−2022=a，2023−n=b，根据完全平方公式计算即可．
本题考查的是整式的化简求值，掌握完全平方公式是解题的关键．

14.【答案】1 
【解析】解：如图，作A关于OC的对称点A′，连接OA′、A′B，则∠AOC=∠A′OC．
∵∠AOC+∠BOC=α，
∴∠A′OC+∠BOC=∠A′OB=α．
∵A′O2=12+22=5，A′B2=12+22=5，OB2=12+32=10，
∴A′O2+A′B2=OB2，A′O=A′B，
∴△A′OB是等腰直角三角形，
∴∠A′OB=45°，
∴tanα=1．
故答案为：1．
作A关于OC的对称点A′，连接OA′、A′B，则∠AOC=∠A′OC，∠AOC+∠BOC=∠A′OC+∠BOC=∠A′OB=α.再证明△A′OB是等腰直角三角形，求出∠A′OB=45°，即可得出tanα=1．
本题考查了解直角三角形，勾股定理及其逆定理，轴对称的性质等知识，准确作出辅助线是解题的关键．

15.【答案】40° 
【解析】解：∵AB是⊙O的直径，PA与⊙O相切于点A，
∴OA⊥PA，
∴∠PAB=90°，
∵∠B=12∠AOC，∠ABC=25°，
∴∠AOC=50°，
∴∠P=180°−∠PAB−∠AOC=40°．
故答案为：40°．
利用圆周角定理，切线的性质定理和三角形的内角和定理解答即可．
本题主要考查了圆周角定理，圆的切线的性质定理，熟练掌握上述定理是解题的关键．

16.【答案】−12 
【解析】解：如图，连接OA，
∵AB⊥x轴，
∴OC//AB，
∴S△OAB=S△CAB=6，
而S△OAB=12|k|，
∴12|k|=6，
∵k<0，
∴k=−12．
故答案为−12．
连接OA，如图，利用三角形面积公式得到S△OAB=S△CAB=6，再根据反比例函数的比例系数k的几何意义得到12|k|=6，然后去绝对值即可得到满足条件的k的值．
本题考查了反比例函数的比例系数k的几何意义：在反比例函数y=kx图象中任取一点，向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是12|k|，且保持不变．

17.【答案】解：两边都乘以x−1，得：x−2+2(x−1)=−2，
解得：x=23，
检验：当x=23时，x−1=−13≠0，
∴方程的解为x=23． 
【解析】两边都乘以x−1，化分式方程为整式方程，解之求得x的值，再检验即可得．
本题主要考查解分式方程，解题的关键是掌握解分式方程的步骤：①去分母；②求出整式方程的解；③检验；④得出结论．

18.【答案】解：原式=−1−3+1
=−3． 
【解析】先去绝对值，算立方根，零指数幂，再算加减．
本题考查实数的混合运算，解题的关键是掌握实数相关的运算法则．

19.【答案】解：2x−4>0①1−2(x−3)>x+1②，
由①得，x>−2，
由②得，x<2，
所以，不等式组的解集是−2 【解析】先求出两个不等式的解集，再求其公共解．
本题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解．求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到(无解)．

20.【答案】78 
【解析】解：(1)树状图：

一共有4种情况，通电的情况有3种，
P(P、Q之间电流通过)=34；

(2)方法同(1)，一共有8种情况，通电的情况有7种，
P(P、Q之间电流通过)=78．
故答案为：78．
(1)根据树状图的画法作出即可，再根据概率公式列式即可得解；
(2)根据(1)的规律，只有全断开时电流不通过，列出电流通过的概率即可．
本题考查了列表法与树状图，用到的知识点为：概率=所求情况数与总情况数之比．

21.【答案】0.25  54  120 
【解析】解：(1)本次抽取的学生有：24÷0.20=120(人)，
a=30÷120=0.25，
b=120×0.45=54，
c=120，
故答案为：0.25，54，120；
(2)由(1)知，b=54，
补全的条形统计图如右图所示；
(3)800×(0.25+0.45)
=800×0.7
=560(人)，
答：估计测试成绩等级在良好以上(包括良好)的学生约有560人．
(1)根据合格的频数和频率，可以计算出本次调查的总人数，然后即可计算出a、b、c的值；
(2)根据(1)中b的值，可以将条形统计图补充完整；
(3)根据统计图中的数据，可以计算出测试成绩等级在良好以上(包括良好)的学生约有多少人．
本题考查条形统计图、频数分布表、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．

22.【答案】(1)证明：∵AB//DE，
∴∠B=∠DEF，
∵AC//DF．
∴∠ACB=∠DFE，
在△ABC和△DEF中，
∠B=DEF∠ACB=DFEAB=DE，
∴△ABC≌△DEF(SAS)，
∴∠ACB=∠F，
∴AC//DF；
(2)解：由(1)得∠B=∠DEF，∠ACB=∠F，
∴∠DEF=∠B=55°，∠EOC=80°，
在△EOC中，∠DEF+∠ACB+∠EOC=180°，
∴∠ACB=180°−∠DEF−∠EOC=180°−55°−80°=45°．
∴∠F=45°． 
【解析】(1)由AB//DE得∠B=∠DEF，根据BE=CF得BC=EF，可证明△CAE≌△DAE(SAS)，根据全等三角形的性质和平行线的性质即可证得结论；
(2)由全等三角形的性质得到∠DEF=55°，∠EOC=80°，根据三角形内角和定理即可求出∠ACB．
本题考查了平行线的性质，全等三角形的判定和性质，三角形内角和定理，根据判定三角形全等的方法证得△ABC≌△DEF是解决问题的关键．

23.【答案】解：(1)设购买绿萝x盆，吊兰y盆，
依题意得：x+y=469x+6y=390，
解得：x=38y=8，
∵8×2=16，16<38，
∴x=38y=8符合题意．
答：购买绿萝38盆，吊兰8盆．
(2)设购买绿萝m盆，则购买吊兰(46−m)盆，
依题意得：m≥2(46−m)，
解得：m≥923，
设购买两种绿植的总费用为w元，则w=9m+6(46−m)=3m+276，
∵3>0，
∴w随m的增大而增大，
又∵m≥923，且m为整数，
∴当m=31时，w取得最小值，最小值=3×31+276=369．
答：购买两种绿植总费用的最小值为369元． 
【解析】本题考查了二元一次方程组的应用、一元一次不等式的应用以及一次函数的应用，解题的关键是：(1)找准等量关系，正确列出二元一次方程组；(2)根据各数量之间的关系，找出w关于m的函数关系式．
(1)设购买绿萝x盆，吊兰y盆，利用总价=单价×数量，结合购进两种绿植46盆共花费390元，即可得出关于x，y的二元一次方程组，解之即可得出结论；
(2)设购买绿萝m盆，则购买吊兰(46−m)盆，根据购进绿萝盆数不少于吊兰盆数的2倍，即可得出关于m的一元一次不等式，解之即可得出m的取值范围，设购买两种绿植的总费用为w元，利用总价=单价×数量，即可得出w关于m的函数关系式，再利用一次函数的性质，即可解决最值问题．

24.【答案】解：∵AB=34cm，BC=70cm，
∴AC=AB+BC=104cm，
在Rt△ACE中，sin∠BCD=AEAC，
∴AE=AC⋅sin∠BCD=104×0.85≈88cm．
答：点A到CD的距离AE的长度约88cm． 
【解析】由AB，BC的长度求出AC长度，然后根据sin∠BCD=AEAC求解．
本题考查解直角三角形，解题关键是掌握锐角三角函数的定义．

25.【答案】解：(1)∵一次函数y1=k1x+b与坐标轴分别交于A(5,0)，B(0,52)两点，
∴5k1+b=0b=52，
解得k1=−12b=52．
∴一次函数的解析式为：y1=−12x+52．
∵△OAP的面积为54，
∴12⋅OA⋅yP=54，
∴yP=12，
∵点P在一次函数图象上，
∴令−12x+52=12.解得x=4，
∴P(4,12).
∵点P在反比例函数y2=k2x的图象上，
∴k2=4×12=2．
∴一次函数的解析式为：y1=−12x+52，反比例函数的解析式为：y2=2x．
(2)令−12x+52=2x，解得x=1或x=4，
∴K(1,2)，
由图象可知，当y2>y1时，x的取值范围为：04；
(3)如图，作点P关于x轴的对称点P′，连接QP′，线段QP′与x轴的交点即为点C，

∵P(4,12)，
∴P′(4,−12)，
∴PP′=1，
∴直线QP′的解析式为：y=−56x+176，
令y=0，解得x=175，
∴C(175,0)，
∴S△PQC=12⋅(xC−xQ)⋅PP′
=12×(175−1)×1
=65，
∴当PC+QC最小时，△PKC的面积为65． 
【解析】(1)根据待定系数法可求出直线AB的解析式，根据△OAP的面积可得出点P的坐标，代入反比例函数解析式可得出反比例函数的解析式；
(2)联立一次函数和反比例函数的解析式，可得出点K的坐标，结合图象可直接得出x的取值范围；
(3)作点P关于x轴的对称点P′，连接KP′，线段KP′与x轴的交点即为点C，求出直线QP′的解析式，令y=0，可得出点C的坐标，再根据三角形的面积公式可得出结论．
本题考查反比例函数与一次函数综合题，掌握待定系数法求函数解析式，数形结合思想，轴对称最值问题，三角形的面积问题等知识，求出一次函数和反比例函数的解析式是解题的关键．

26.【答案】解：(1)在线段AB上取一点R，使BR=BE，连接RE，则△BRE是等腰直角三角形，
∴∠BRE=45°，
∴∠ARE=135°，
∵CG平分∠DCF，
∴∠GCF=45°，
∴∠ECG=135°，
∴∠ARE=∠ECG，
∵EG⊥AE，
∴∠BEA+∠CEG=90°，
又∵∠BAE+∠BEA=90°，
∴∠BAE=∠CEG，
∴△ARE∽△ECG，
∴AEEG=AREC，
∵E是BC的中点，
∴BE=CE，AR=AB−BR=AB−BE，
∵ABBE=k，
∴AB=kBE，
∴AR=kBE−BE=(k−1)BE，
∴AEEG=(k−1)BEBE=k−1；

(2)∵∠EAH=∠GAE，∠AHE=∠AEG=90°，
∴△AHE∽△AEG，
∴AHAE=HEEG，
∴AHHE=AEEG，
∵∠AHE=90°，
∴∠AHD+∠EHC=90°，
∵∠AHD+∠HAD=90°，
∴∠EHC=∠HAD，
∵∠ADH=∠HCE=90°，
∴△ADH∽△HCE，
∴AHHE=ADEC=BCEC=2，
∴AGEG=2，
∴k−1=2，
∴k=3；

(3)过点P作PQ⊥AE于Q，过Q作MN//AD分别交AB，CD于M，N，

设BE=2x=EC，
则AB=6x，
由△AMQ与△QNP全等，
设MQ=n，
∵tan∠BAE=13，
∴AM=3n=QN，
∴n+3n=4x，
∴n=x，
∴MQ=x，AQ= 10x=PQ，
∴QE=AE−QA= 10x，
由(2)知，AE：EG=k−1=2，
∴EG= 10x，
∴EG=PQ，
∵EG⊥AE，
∴PQ//EG，
∴四边形QEGP是平行四边形，
∵QE=EG，∠PQE=90°，
∴四边形QEGP是正方形，
∴PG= 10x= 5，
∴x= 22，
∴BC=4x=2 2． 
【解析】(1)在AB上截BR=BE，根据矩形的性质和AE⊥EG，判定△ARE与△ECG相似，根据相似三角形的性质解答即可；
(2)根据(1)中的证明方法解答即可；
(3)延长AP，EG交于点Q，过点Q作QM⊥CF于点M，过点Q作QN⊥DC于点N，根据等腰直角三角形的判定得出△AEQ是等腰直角三角形，进而利用全等三角形的判定和性质解答即可．
本题是相似形的综合题，考查了相似三角形的判定和性质，正方形的判定和性质，矩形的性质，正确地作出辅助线是解题的关键．

27.【答案】解：(1)把A(−2,0)、B(1,0)代入y=ax2+x+c得：
4a−2+c=0a+1+c=0，
解得a=1c=−2，
∴抛物线L1对应的函数表达式为y=x2+x−2；
(2)在y=x2+x−2中，令x=0得y=−2，
∴C(0,−2)，
由A(−2,0)，C(0,−2)得直线AC解析式为y=−x−2，
设D(m,m2+m−2)，则N(m,−m−2)，
∴DN=−m−2−(m2+m−2)=−m2−2m，
∵OA=OC=2，
∴△AOC是等腰直角三角形，
∴∠ACO=45°，
∵DN//OC，
∴∠DNM=∠ACO=45°，
∴△DNM是等腰直角三角形，
∴DM= 22DN，
∴DM= 22(−m2−2m)=− 22m2− 2m=− 22(m+1)2+ 22，
∵− 22<0，
∴当m=−1时，DM取最大值 22，此时D的坐标为(−1,−2)；
∴线段DM的最大值是 22，此时点D的坐标为(−1,−2)；
(3)过A作AH⊥CP于H，过H作KR//y轴交x轴于K，过C作CR⊥KR于R，如图：

∵tan∠ACP=13，
∴AHCH=13，
∵∠AHK=90°−∠CHR=∠HCR，∠AKH=∠CRH=90°，
∴△AKH∽△HRC，
∴AKHR=HKCR=AHCH=13，
∴HR=3AK，CR=3HK，
设AK=p，HK=q，则HR=3p，CR=3q，
∵CR=OK=OA+AK，HK+HR=OC，
∴3q=2+pq+3p=2，
解得p=25q=45，
∴H(−125,−45)，
由H(−125,−45)，C(0,−2)得直线HC解析式为y=−12x−2，
联立y=−12x−2y=x2+x−2，
解得x=0y=−2或x=−32y=−54，
∴P(−32,−54)，
∵y=x2+x−2=(x+12)2−94，将抛物线y=x2+x−2沿着x轴向左平移后得到抛物线L2，
∴设抛物线L2解析式为y=(x+t)2−94，
将P(−32,−54)代入y=(x+t)2−94得：
−54=(−32+t)2−94，
解得t=52或t=12(舍去)，
∴抛物线L2对应的函数表达式为y=(x+52)2−94． 
【解析】(1)用待定系数法可得抛物线L1对应的函数表达式为y=x2+x−2；(2)求出C(0,−2)，直线AC解析式为y=−x−2，设D(m,m2+m−2)，可得DN=−m−2−(m2+m−2)=−m2−2m，而OA=OC=2，可推得△DNM是等腰直角三角形，DM= 22DN，故DM= 22(−m2−2m)=− 22m2− 2m=− 22(m+1)2+ 22，由二次函数性质可得答案；
(3)过A作AH⊥CP于H，过H作KR//y轴交x轴于K，过C作CR⊥KR于R，由tan∠ACP=13，证明△AKH∽△HRC，得AKHR=HKCR=AHCH=13，设AK=p，HK=q，可得3q=2+pq+3p=2，从而H(−125,−45)，直线HC解析式为y=−12x−2，联立y=−12x−2y=x2+x−2，解得P(−32,−54)，设抛物线L2解析式为y=(x+t)2−94，解得t=52或t=12(舍去)，故抛物线L2对应的函数表达式为y=(x+52)2−94．
本题考查二次函数的综合应用，涉及待定系数法，等腰三角形的判定与性质，相似三角形的判定与性质，平移变换，锐角三角函数等知识，解题的关键是用含字母的式子表示相关点的坐标和相关线段的长度．