2023年山东省烟台市莱阳市中考数学二模试卷（含解析）

这是一份2023年山东省烟台市莱阳市中考数学二模试卷（含解析），共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2023年山东省烟台市莱阳市中考数学二模试卷
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列说法正确的是(    )
A. 2的倒数是−2 B. 3的相反数是13
C. 绝对值最小的数是1 D. 0的相反数是0
2. 2023年2月24日，“逐梦寰宇问苍穹——中国载人航天工程三十年成就展”在中国国家博物馆展出，下列航天图标中，是中心对称图形的是(    )
A. B.
C. D.
3. 下列计算正确的是(    )
A. x3−x2=x B. x3+x3=x6 C. (x3)3=x9 D. x6÷x3=x2
4. 孙悟空是中国明代小说家吴承恩的著作《西游记》中的角色之一，它会七十二变、筋斗云，一个筋斗能翻十万八千里(1里0.5km).将十万八千里用科学记数法可表示为(    )
A. 5.4×107m B. 1.08×105m C. 5.4×104m D. 5.4×108m
5. 体育课上，体育老师随机抽取了某班10名男生的引体向上成绩，将这组数据整理后制成如下统计表，则关于这组数据下列说法正确的是(    )
成绩/个
9
8
6
5
人数
2
3
3
2

A. 方差是2.2 B. 中位数是8 C. 众数是8 D. 平均数是8
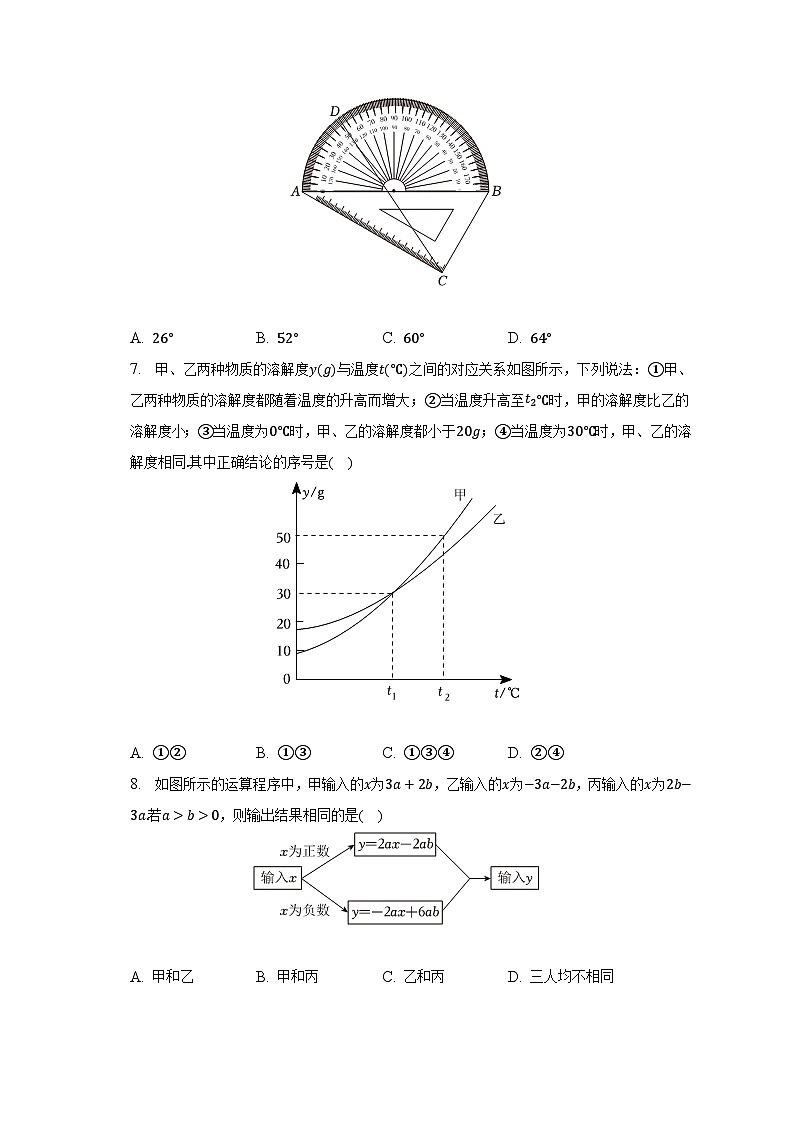
6. 如图，一块直角三角板ABC的斜边AB与量角器的直径重合，点D对应的刻度值为52°，则∠BCD的度数为(    )

A. 26° B. 52° C. 60° D. 64°
7. 甲、乙两种物质的溶解度y(g)与温度t(℃)之间的对应关系如图所示，下列说法：①甲、乙两种物质的溶解度都随着温度的升高而增大；②当温度升高至t2℃时，甲的溶解度比乙的溶解度小；③当温度为0℃时，甲、乙的溶解度都小于20g；④当温度为30℃时，甲、乙的溶解度相同.其中正确结论的序号是(    )

A. ①② B. ①③ C. ①③④ D. ②④
8. 如图所示的运算程序中，甲输入的x为3a+2b，乙输入的x为−3a−2b，丙输入的x为2b−3a.若a>b>0，则输出结果相同的是(    )

A. 甲和乙 B. 甲和丙 C. 乙和丙 D. 三人均不相同
9. 自然界中存在许多斐波那契螺旋线图案.斐波那契螺旋线，也称“黄金螺旋线”，是根据斐波那契数1，1，2，3，5，8，13，……画出螺旋曲线.在平面直角坐标系中，依次以这组数为半径作90°的圆弧P1P2，P2P3，P3P4…，得到一组螺旋线，连接P1P2，P2P3，P3P4，⋯，得到一组螺旋折线，如图所示.已知点P1，P2，P3的坐标分别为(−1,0)，(0,1)，(1,0)，则点P7的坐标为(    )


A. (6,1) B. (8,0) C. (8,2) D. (9,−2)
10. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示，图象过点(−1,0)，对称轴为直线x=2，下列结论：(1)4a+b=0；(2)9a+c>3b；(3)8a+7b+2c>0；(4)若点A(−3,y1)、点B(−12,y2)、点C(72,y3)在该函数图象上，则y1

A. 2个 B. 3个 C. 4个 D. 5个
二、填空题（本大题共6小题，共18.0分）
11. 枫叶一般呈掌状五裂型，裂片具有少数突出的齿.小明将一个枫叶标本放在平面直角坐标系中如图，表示叶片“顶”A，B两点的坐标分别为(−2,2)，(−3,0)，则叶柄“底部”点C的坐标为______ ．


12. 在螳螂的示意图中，AB//DE，△ABC是等腰三角形，∠ABC=126°，∠CDE=72°，则∠ACD的度数是______ ．


13. 图①是艺术家埃舍尔的作品，他将数学与绘画完美结合，在平面上创造出立体效果．图②是一个菱形，将图②截去一个边长为原来一半的菱形得到图③，用图③镶嵌得到图④，将图④着色后，再次镶嵌便得到图①，则图④中∠ABC的度数是______°.


14. 幻方历史很悠久，传说最早出现在夏禹时代的“洛书”.根据幻方的相等关系设计出来一个“幻圆”，即大圆、小圆、横线、竖线上的四个数字加起来的和都相等.如图给出了部分数字，则幻圆中x−y的值为______ ．


15. 七巧板是古代中国劳动人民的发明，是一种古老的中国传统智力游戏，其历史至少可以追溯到公元前一世纪.小明将一个边长为4的正方形制作成一副如图1所示的七巧板，取出其中的六块，拼成了一个▱ABCD(如图2)，则▱ABCD的对角线AC的长度为______ ．

16. 如图1，在▱ABCD中，∠B=60°，BC=2AB，动点E从点A出发，以每秒1个单位的速度沿线段AB运动到点B停止，同时动点F从点B出发，以每秒4个单位的速度沿折线B−C−D运动到点D停止.图2是点E，F运动时，△BEF的面积S与运动时间t函数关系的图象，则a的值是______ ．

三、解答题（本大题共8小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题6.0分)
计算：
(1)(1− 3)0−|− 2|+3−27−(−12)−1；
(2)4sin60°⋅cos30°+13tan260°− 2⋅cos45°．
18. (本小题6.0分)
如图，在△ABC中，点D、E分别是边AC、AB的中点，点F在线段DE上，AB=5，BF=4，AF=3，BC=7，求DF的长度．

19. (本小题9.0分)
春暖花开正是郊游踏青的好时节.为开阔学生视野，一班的家委会准备利用周末组织该班学生参加郊游活动，计划在某商家采购A、B两种水果各600元，其中A种水果比B种水果多买20千克，该商家B种水果的单价是A种水果单价的1.5倍．
(1)求A、B两种水果的单价分别是多少元？
(2)经过家委会和商家协商，商家决定给该班购买的A、B两种水果进行优惠，将A、B两种水果都打8折，因此，家长将调整购买计划，购买A、B两种水果共150千克，但购买的总费用不能超过1500元，则至少购买A种水果多少千克？
20. (本小题9.0分)
某校九年级体育期末检测自选项目有篮球、跳绳、立定跳远，每个学生任选一项为自选考试项目．

(1)求学生甲与乙至少有一人自选篮球的概率；
(2)除自选项目以外，长跑为必考项目，校内体育活动表现是必查项目，学生甲与乙的期末体育各项成绩(百分制)的统计图表如图所示：
考生
自选项目
长跑
校内体育活动
甲
95
100
95
乙
100
95
95
①补全条形统计图；
②如果期末体育考试成绩按照扇形统计图(图2)各项所占之比计算(百分制)，请通过计算说明甲、乙两人谁的期末体育成绩高．
21. (本小题9.0分)
一盏可调节台灯的平面示意图如图所示，底座固定杆OA与底座OE垂直，AB为固定支撑杆，BC为可绕着点B旋转的调节杆，若，求台灯灯罩C到水平面OE的距离.(结果精确到0.1，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，sin27°≈0.45，cos27°≈0.89，tan27°≈0.51)

22. (本小题9.0分)
如图，在Rt△ABC中，∠ACB=90°，以斜边AB上的中线CD为直径作⊙O，与BC交于点F，与AB的另一个交点为E，过F作FG⊥AB，垂足为G．
(1)求证：FG是⊙O的切线；
(2)若⊙O的直径为5，sinB=35，求ED的长．

23. (本小题12.0分)
已知AE//BF，AB=6，点C为射线BF上一动点(不与点B重合)，△BAC关于AC的轴对称图形为△DAC．

(1)如图1，当点D在射线AE上时，求证：四边形ABCD是菱形；
(2)如图2，当点D在射线AE，BF之间时，若点G为射线BF上一点，点C为BG的中点，连接BD交AC于点M，BG=10，AC=5．
①求证：△BDG为直角三角形；
②求DG的长．
24. (本小题12.0分)
如图，在平面直角坐标系中，抛物线y=12x2+bx+c(b、c为常数)的顶点坐标为(32,−258)，与x轴交于A、B两点(点A在点B左侧)，与y轴交于点C，点C与点D关于x轴对称，连接AD，作直线BD．

(1)求点A和点B的坐标；
(2)求证：∠ADO=∠DBO；
(3)点P在抛物线y=12x2+bx+c上，点Q在直线BD上，当以点C、D、P、Q为顶点的四边形为平行四边形时，直接写出点Q的坐标．
答案和解析

1.【答案】D 
【解析】解：A、2的倒数是12，故A不符合题意；
B、3的相反数是−3，故B不符合题意；
C、绝对值最小的数是0，故C不符合题意；
D、0的相反数是0，正确，故D符合题意．
故选：D．
乘积是1的两数互为倒数，只有符号不同的两个数叫做互为相反数，有理数的绝对值都是非负数，由此即可得到答案．
本题考查倒数，相反数，绝对值，关键是掌握倒数、相反数的定义，绝对值的意义．

2.【答案】C 
【解析】解：由题意知，图形是中心对称图形，
故选：C．
根据在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形得出结论即可．
本题主要考查中心对称的知识，熟练掌握中心对称的概念是解题的关键．

3.【答案】C 
【解析】解：A、x3与−x2不属于同类项，不能合并，故A不符合题意；
B、x3+x3=2x3，故B不符合题意；
C、(x3)3=x9，故C符合题意；
D、x6÷x3=x3，故D不符合题意；
故选：C．
利用合并同类项的法则，同底数幂的除法的法则，幂的乘方的法则对各项进行运算即可．
本题主要考查合并同类项，幂的乘方，同底数幂的除法，解答的关键是对相应的运算法则的掌握．

4.【答案】A 
【解析】解：∵十万八千里即108000里，
∴108000×0.5×1000=54000000(m)=5.4×107(m)，
故选：A．
将一个数表示成a×10n的形式，其中1≤|a|<10，n为整数，这种记数方法叫做科学记数法，结合题意列式计算后据此即可得出答案．
本题考查科学记数法表示较大的数，此为基础且重要知识点，必须熟练掌握．

5.【答案】A 
【解析】解：根据题目给出的数据，可得：
平均数为：110×(9×2+8×3+6×3+5×2)=7，故D选项不符合题意；
方差是：110×[2×(9−7)2+(8−7)2×3+(6−7)2×3+(5−7)2×2]=2.2，故A选项符合题意；
中位数是：8+62=7，故B选项不符合题意；
众数是：8和6，故C选项不符合题意；
故选：A．
根据方差，中位数，众数，平均数的定义分别计算出结果，然后判断即可．
本题考查的是平均数，众数，中位数和方差，熟练掌握平均数，众数，中位数，方差的计算公式是解题的关键．

6.【答案】D 
【解析】解：设AB的中点为O，连接OD，

∵∠AOD=52°，
∴∠ACD=12∠AOD=26°，
∵∠ACB=90°，
∴∠BCD=∠ACB−∠ACD=64°，
故选：D．
设AB的中点为O，连接OD，根据圆周角定理可得∠ACD=12∠AOD=26°，然后利用角的和差关系进行计算，即可解答．
本题考查了圆周角定理，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．

7.【答案】B 
【解析】解：由图象可以看出，
①甲、乙两种物质的溶解度都随着温度的升高而增大，说法正确；
②当温度升高至t2℃时，甲的溶解度比乙的溶解度大，原说法错误；
③当温度为0℃时，甲、乙的溶解度都小于20g，说法正确；
④当温度为t1℃时，甲、乙的溶解度相同，原说法错误．
所有正确结论的序号是①③．
故选：B．
先对图象的交点及在一点范围内图象的性质进行分析，然后再对各条信息逐一判断即可．
本题主要考查了函数的图象，熟练掌握横纵坐标表示的意义是解题的关键．

8.【答案】B 
【解析】解：∵a>b>0
∴3a+2b>0，−3a−2b<0，2b−3a<0
∴甲输出的结果为：y=2a(3a+2b)−2ab=6a2+2ab；
乙输出的结果为：y=−2a(−3a−2b)+6ab=6a2+10ab；
丙输出的结果为：y=−2a(2b−3a)+6ab=6a2+2ab；
输出结果相同的是甲和丙，
故选：B．
先判断3a+2b>0，−3a−2b<0，2b−3a<0，分别计算输出的结果得到答案．
本题考查整式的乘法运算，掌握运算法则是解题的关键．

9.【答案】D 
【解析】解：观察发现：P1(−1,0)先向右平移1个单位，再向上平移1个单位得到P2(0,1)；
P2(0,1)先向右平移1个单位，再向下平移1个单位得到P3(1,0)；
P3(1,0)先向左平移2个单位，再向下平移2个单位得到P4(−1,−2)；
P4(−1,−2)先向左平移3个单位，再向上平移3个单位得到P5(−4,1)；
P5(−4,1)先向右平移5个单位，再向上平移5个单位得到P6(1,6)．
根据斐波那契数，P6(1,6)应先向右平移8个单位，再向下平移8个单位得到P7(9,−2)．
故选：D．
观察图象，找出每个点的运动轨迹与斐波那契数结合推出P7的位置，即可解决问题．
本题考查在平面直角坐标系中的点的坐标规律．考查了学生数形结合的能力，解题的关键是找出每个点的坐标及运动规律，推出答案即可．在做题时一定要理解题意．

10.【答案】B 
【解析】解：(1)正确．
∵−b2a=2，
∴4a+b=0.故正确．
(2)错误．
∵x=−3时，y<0，
∴9a−3b+c<0，
∴9a+c<3b，故(2)错误．
(3)正确．由图象可知抛物线经过(−1,0)和(5,0)，
∴a−b+c=025a+5b+c=0解得b=−4ac=−5a，
∴8a+7b+2c=8a−28a−10a=−30a，
∵a<0，
∴8a+7b+2c>0，故(3)正确．
(4)错误，
∵点A(−3,y1)、点B(−12,y2)、点C(72,y3)，
∵72−2=32，2−(−12)=52，
∴32<52
∴点C离对称轴的距离近，
∴y3>y2，
∵a<0，−3<−12<2，
∴y1 ∴y1 (5)正确．
∵a<0，
∴(x+1)(x−5)=−3a>0，
即(x+1)(x−5)>0，
故x<−1或x>5，故(5)正确．
∴正确的有3个，
故选：B．
(1)正确．根据对称轴公式计算即可．
(2)错误，利用x=−3时，y<0，即可判断．
(3)正确．由图象可知抛物线经过(−1,0)和(5,0)，列出方程组，用a表示出b、c即可判断．
(4)错误．利用函数图象即可判断．
(5)正确．利用二次函数与二次不等式关系即可解决问题．
本题考查二次函数与系数关系，灵活掌握二次函数的性质是解决问题的关键，学会利用图象信息解决问题，属于中考常考题型．

11.【答案】(2,−3) 
【解析】解：∵A，B两点的坐标分别为(−2,2)，(−3,0)，
∴得出坐标轴如下图所示位置：

∴点C的坐标为(2,−3)．
故答案为：(2,−3)．
根据A，B的坐标确定出坐标轴的位置，点C的坐标可得．
本题主要考查了用坐标确定位置，和由点的位置得到点的坐标．依据已知点的坐标确定出坐标轴的位置是解题的关键．

12.【答案】45° 
【解析】解：延长ED交AC于点F，

∵△ABC是等腰三角形，∠ABC=126°，
∴∠A=∠ACB=180°−126°2=27°，
∵AB//DE，
∴∠CFD=∠A=27°，
∵∠CDE是△CFD的一个外角，
∴∠CDE=∠CFD+∠ACD，
∵∠CDE=72°，
∴72°=27°+∠ACD，
∴∠ACD=45°，
故答案为：45°．
根据△ABC是等腰三角形，∠ABC=126°即可求出∠A的度数，再根据平行线的性质即可求出∠CFD的度数，再根据三角形外角的性质即可求出∠ACD的度数．
本题考查了三角形内角和定理，平行线的性质，三角形外角的性质，等腰三角形的性质，熟练掌握这些性质是解题的关键．

13.【答案】60 
【解析】解：如图，

∵∠BAD=∠BAE=∠DAE，∠BAD+∠BAE+∠DAE=360°，
∴∠BAD=∠BAE=∠DAE=120°，
∵BC//AD，
∴∠ABC=180°−120°=60°，
故答案为：60．
先确定∠BAD的度数，再利用菱形的对边平行，利用平行线的性质即可求出∠ABC的度数．
本题考查了菱形的性质与学生读题审题的能力，理解题意，准确识图，求出∠BAD的度数是解题关键．

14.【答案】5 
【解析】解：根据题意得：x+3−1=4+y+3，
∴x−y=5．
故答案为：5．
根据大圆、小圆、横线、竖线上的四个数字加起来的和都相等，可得出关于x，y的二元一次方程，整理后，即可求出x−y的值．
本题考查了二元一次方程的应用以及数学常识，找准等量关系，正确列出二元一次方程是解题的关键．

15.【答案】 58 
【解析】解：如图，
延长CB到点E，过点A作AE⊥CB，
根据七巧板的特点可知，AB=4，BF= 2×12×4=2 2，FC=12BF= 2，
△ABF为等腰直角三角形，
∴∠ABF=45°，
∴∠ABE=45°，
∵∠AEB=90°，
所以△ABE是等腰直角三角形，
AE=BE=4 2=2 2，
CE=BE+BC=2 2+2 2+ 2=5 2，
∴AC= AE2+CE2= 58．
故答案为： 58．
根据七巧板的特性找出线段之间的关系，构造直角三角形，利用勾股定理求出对角线的长度．
本题以正方形为背景考查了正方形与等腰直角三角形的灵活运用，考查学生在几何中根据图形找出内在的线段关系的能力．本题难度之中，解决问题的关键是弄清几何条件，构造直角三角形，利用勾股定理求出答案．

16.【答案】9 3 
【解析】解：由题意得：当E运动到B时，S为0，当E运动AB中点时，F到C点处，此时S最大为a，
∴AB=6，∴BC=2AB=12，
∴S=12×12×3×sin60°=18× 32=9 3，
故答案为：9 3．
由题意得：当E运动到B时，S为0，当E运动AB中点时，F到C点处，此时S最大为a，再根据三角形的面积公式求解．
本题考查了动点问题的函数图象，掌握三角形的面积公式是解题的关键．

17.【答案】解：(1)(1− 3)0−|− 2|+3−27−(−12)−1
=1− 2−3+2
=− 2；
(2)4sin60°⋅cos30°+13tan260°− 2⋅cos45°
=4× 32× 32+13×( 3)2− 2× 22
=3+1−1
=3． 
【解析】(1)本题涉及零指数幂、负整数指数幂、绝对值、立方根4个考点．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果；
(2)先将特殊角的三角函数值代入，再根据实数的运算法则求得计算结果．
本题主要考查了实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值、特殊角的三角函数值等考点的运算．

18.【答案】解：∵点D、E分别是边AC、AB的中点，
∴DE是△ABC的中位线，
∴DE=12BC=3.5，
∵AB=5，BF=4，AF=3，
∴BF2+AF2=32+42=25=52=AB2，
∴△ABF是直角三角形，即∠AFB=90°，
∴EF=12AB=2.5，
∴DF=DE−EF=1． 
【解析】由三角形中位线定理得到DE=3.5，再证明△ABF是直角三角形，即∠AFB=90°，即可利用直角三角形斜边上的中线等于斜边的一半求出EF=2.5，则DF=DE−EF=1．
本题主要考查了三角形中位线定理，勾股定理的逆定理，直角三角形斜边上的中线的性质，证明△ABF是直角三角形是解题的关键．

19.【答案】解：(1)设该商家A种水果的单价是x元，
根据题意得：600x−6001.5x=20，
解得：x=10，
经检验，x=10是所列方程的解，
∴1.5x=1.5×10=15．
答：A种水果的单价是10元，B种水果的单价是15元．
(2)设购买A种水果m千克，
根据题意得：10×0.8m+15×0.8(150−m)≤1500，
解得：m≥75，
∴m的最小值为75．
答：至少购买A种水果75千克． 
【解析】(1)设该商家A种水果每千克的售价是x元，则B种水果每千克的售价是1.5x元，利用数量=总价÷单价，结合用600元购买A种水果数量比用600元购买B种水果数量多20千克，可得出关于x的分式方程，解之经检验后，可得出A种水果每千克的售价，再将其代入1.5x中，即可求出B种水果每千克的售价；
(2)设购买m千克A种水果，则购买(150−m)千克B种水果，利用总价=单价×数量，结合总价不超过1500元，可得出关于m的一元一次不等式，解之取其中的最小值，即可得出结论．
本题考查了分式方程的应用以及一元一次不等式的应用，解题的关键是：(1)找准等量关系，正确列出分式方程；(2)根据各数量之间的关系，正确列出一元一次不等式．

20.【答案】解：(1)把篮球、跳绳、立定跳远分别记为A、B、C，画树状图如图：

一共有12种等可能的结果，其中甲与乙至少有一个人自选篮球的结果有5种，
∴P(甲与乙至少有一人自选篮球)=59；
(2)①补全条形统计图如下：

②∵扇形统计图中自选项目的圆心角为：360°−108°−72°=180°，
∴自选项目：长跑：校内体育活动表现=180°：108°：72°=5：3：2，
甲的期末体育成绩为：
95×55+3+2+100×35+3+2+95×25+3+2=96.5(分)，
乙的期末体育成绩为：
100×55+3+2+95×35+3+2+95×25+3+2=97.5(分)，
∵96.5<97.5，
∴乙的期末体育成绩高． 
【解析】(1)利用列表法或树状图法列举出所有等可能的结果，从中找出甲与乙至少有一人自选篮球的结果数，再利用等可能事件的概率公式求出即可；
(2)①根据统计表中乙校内体育活动得分补全条形统计图即可；
②分别求出甲，乙成绩的平均数，比较即可．
本题考查条形统计图，扇形统计图，加权平均数，用列表法和树状图法求等可能事件的概率，能从统计图中获取有用信息，掌握列表法和树状图法求等可能事件的概率的方法是解题的关键．

21.【答案】解：过点C作CM⊥OE于M，过B作BN⊥CM于N，延长OA交BN于P，
∵∠OAB=143°，
∴∠BAP=180°−∠OAB=37°，
在Rt△BAP中AB=30，
cos∠BAP=APAB,AP≈AB×0.80=24，
∴OP=OA+AP=8+24=32，
∵BN⊥CM，CM⊥OE，OA⊥OE，
∴∠POM=∠OMN=∠MNP=90°，
∴四边形POMN为矩形，
∴MN=OP=32，∠APN=90°，
∵∠BAP=37°，
∴∠ABP=90°−∠BAP=53°，
∵∠CBA=80°，
∴∠CBN=∠CBA−∠ABP=27°，
在Rt△CBN中B=35，sin∠CBN=CNBC，
∴CN=BC×sin27°≈35×0.45=15.75，
∴CM=MN+CN=32+15.75≈47.8，
答：C到水平面OE的距离约为47.8cm． 
【解析】过点C分别作垂线，在直角三角形中，根据三角比，分别求出AP，CN进而求出CM．
本题考查解直角三角形，解题的关键是作辅助线构造直角三角形．

22.【答案】(1)证明：连接OM，如图1，

∵OC=OF，
∴∠OCF=∠OFC，
在Rt△ABC中，CD是斜边AB上的中线，
∴CD=12AB=BD，
∴∠DCB=∠DBC，
∴∠OFC=∠DBC，
∴OF//BD，
∵FG⊥BD，
∴OF⊥FG，
∵OF过O，
∴FG是⊙O的切线；
(2)解：连接DM，CE，

∵CD是⊙O的直径，
∴∠CED=90°，∠DFC=90°，
即DF⊥BC，CE⊥AB，
由(1)知：BD=CD=5，
∴F为BC的中点，
∵sinB=35，
∴cosB=45，
在Rt△BMD中，BF=BD⋅cosB=4，
∴BC=2BF=8，
在Rt△CEB中，BE=BC⋅cosB=325，
∴ED=BE−BD=325−5=75． 
【解析】(1)连接OM，求出OF//BD，求出OF⊥MG，根据切线的判定推出即可；
(2)连接DF和CE，求出DF⊥BC，CE⊥BD，解直角三角形求出BC和BE，再求出答案即可．
本题考查了切线的判定，圆周角定理，等腰三角形的性质和判定，解直角三角形等知识点，能综合运用知识点进行推理是解此题的关键．

23.【答案】(1)证明：∵△BAC关于AC的轴对称图形为△DAC，
∴∠ACB=∠ACD，AB=AD，BC=DC，
∵AD//BC，
∴∠ACB=∠CAD，
∴∠CAD=∠ACD，
∴AD=CD，
∴AB=AD=BC=CD，
∴四边形ABCD是菱形．
(2)①证明：∵△BAC关于AC的轴对称图形为△DAC，
∴AC⊥BD，BM=DM，
∴∠AMD=90°，
∵C是BG的中点，
∴CM//DG，
∴∠BDG=∠AMD=90°，
∴△BDG是直角三角形；
②解：∵BM=DM，C是BG的中点，BG=10，
∴CM是△BDG的中位线，
∴DG=2CM,CD=BC=12BG=5,AD=AB=6，
设CM=x，
∵AC=5，
∴AM=5−x，
在Rt△AMD中，DM2=AD2−AM2，
在Rt△CMD中，DM2=CD2−CM2，
∴AD2−AM2=CD2−CM2，
即62−(5−x)2=52−x2，
解得：x=75，
∴CM=75，
∴DG=2CM=145． 
【解析】(1)根据轴对称图形的性质得到∠ACB=∠ACD，AB=AD，BC=DC，根据平行线的性质推出∠CAD=∠ACD，根据等腰三角形的判定得出AD=CD，则AB=AD=BC=CD，根据菱形的判定定理即可得解；
(2)①根据轴对称图形的性质得到AC⊥BD，BM=DM，则CM是△BDG的中位线，根据三角形中位线性质得出CM//DG，根据平行线的性质及直角三角形的判定即可得解；
②根据三角形中位线的判定与性质及直角三角形的性质求出DG=2CM,CD=BC=12BG=5,AD=AB=6，设C=x，则AM=5−x，根据勾股定理推出62−(5−x)2=52−x2，据此求出x=75，根据三角形中位线性质即可得解．
此题是四边形综合题，考查了轴对称图形的性质、三角形中位线的判定与性质、等腰三角形的判定、勾股定理等知识，熟练运用轴对称图形的性质、三角形中位线的判定与性质、等腰三角形的判定、勾股定理是解题的关键．

24.【答案】(1)解：由题意得y=12(x−32)2−258=12x2−32x−2，
由12x2−32x−2=0，
得x1=4，x2=−1，
∴点A的坐标为(−1,0)，点B的坐标为(4,0)；
(2)证明：由抛物线的表达式知：点C(0,−2)，则点D(0,2)，
∴OD=2，OB=4，OA=1，
∵ODOB=24=12=OAOD,∠AOD=∠BOD=90°，
∴△DOB∽△AOD．
∴∠ADO=∠DBO；
(3)解：设点Q(m,−12m+2)，点P(m,n)，n=12m2−32m−2，
当CD为平行四边形的对角线时，由中点坐标公式得：
0+0=t+m−2+2=n−12t+2，
整理得：12m2=m，
解得：m=0(舍去)或2，
则t=−2，即点Q(−2,3)；
当CQ是平行四边形的对角线时，同理可得：
0+t=0+m−2−12t+2=n+2，
解得：m=2t=2，
即点Q(2,1)；
当CP是平行四边形的对角线时，同理可得：
0+m=0+t−2+n=2−12t+2，
解得：t=m=1± 17，
综上，点Q的坐标为：(1+ 17,3− 172)或(1− 17,3+ 172)或(−2,3)或(2,1)． 
【解析】(1)令y=12(x−32)2−258=12x2−32x−2=0，解得x=4或−1，即可求解；
(2)由tan∠ADO=OAOD=12，tan∠DBO=ODOB=24=12=tan∠ADO，即可求解；
(3)当CD为平行四边形的对角线时，由中点坐标公式列出方程组，进而求解；当CQ、CP是平行四边形的对角线时，同理可解．
本题是二次函数的综合题，主要考查了利用待定系数法求抛物线的解析式，解直角三角形，平行四边形的性质，综合性较强，难度适中．运用数形结合、分类讨论及方程思想是解题的关键．