2022-2023学年海南省海口市部分校八年级（下）期末数学试卷（B卷）（含解析）

这是一份2022-2023学年海南省海口市部分校八年级（下）期末数学试卷（B卷）（含解析），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年海南省海口市部分校八年级（下）期末数学试卷（B卷）
一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）
1. 约分−2xy2x2y的结果是(    )
A. −2 B. −4yx C. 2yx D. −2yx
2. 计算aa−3+33−a的结果是(    )
A. 1 B. −1 C. 2 D. −2
3. 数据0.000056用科学记数法表示为(    )
A. 56×10−5 B. 5.6×10−5 C. 5.6×10−4 D. 5.6×105
4. 点P(4,−3)关于y轴对称的点的坐标为(    )
A. (−4,3) B. (−4,−3) C. (4,3) D. (−3,4)
5. 将直线y=x平移，使得它经过点(−2,0)，则平移后的直线为(    )
A. y=x−2 B. y=x+1 C. y=−x−2 D. y=x+2
6. 已知点A(−2,a)，B(−1,b)，C(3,c)都在函数y=−6x的图象上，则a、b、c的大小关系是(    )
A. a 7. 小颖八年级第一学期的数学成绩分别为：平时90分，期中90分，期末85分．若这三项成绩分别按1：3：6的比例计入总评成绩，则小颖该学期总评成绩为(    )
A. 86分 B. 87分 C. 88分 D. 89分
8. 如图，在▱ABCD中，∠BAC=68°，∠ACB=36°，则∠D等于(    )


A. 68° B. 72° C. 76° D. 104°
9. 如图，在菱形ABCD中，E是BC的中点，AE⊥BC，连接AC，则∠BAD等于(    )
A. 60°
B. 100°
C. 110°
D. 120°
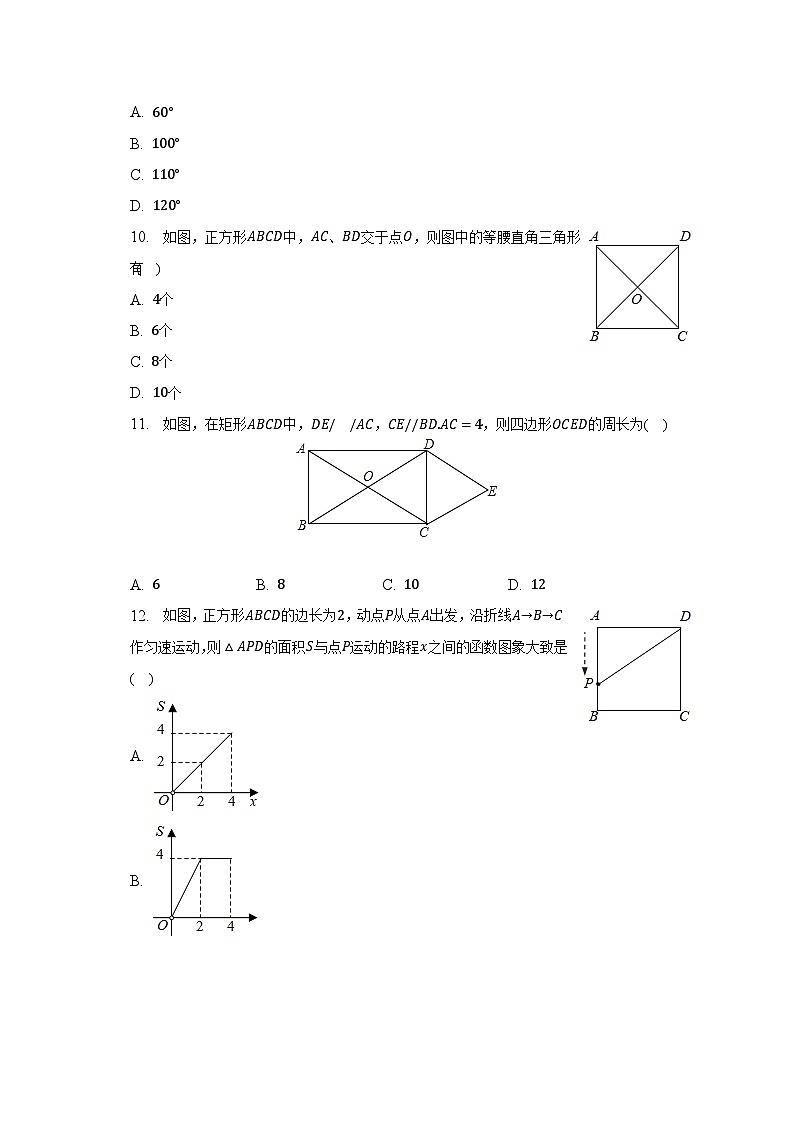
10. 如图，正方形ABCD中，AC、BD交于点O，则图中的等腰直角三角形有(    )
A. 4个
B. 6个
C. 8个
D. 10个
11. 如图，在矩形ABCD中，DE/​/AC，CE//BD.AC=4，则四边形OCED的周长为(    )

A. 6 B. 8 C. 10 D. 12
12. 如图，正方形ABCD的边长为2，动点P从点A出发，沿折线A→B→C作匀速运动，则△APD的面积S与点P运动的路程x之间的函数图象大致是(    )
A.
B.
C.
D.
二、填空题（本大题共4小题，共16.0分）
13. 方程3x=2x−1的解是______．
14. 已知一根弹簧在不挂重物时长6cm，在一定的弹性限度内，每挂1kg重物弹簧伸长0.3cm.则该弹簧总长y(cm)随所挂物体质量x(kg)变化的函数关系式为___          __ ．
15. 如图，矩形ABOC的面积为6，若反比例函数y=kx的图象经过点A，则k的值为______．


16. 如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于12AB的长为半径画弧，两弧相交于C、D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是______ ．


三、解答题（本大题共6小题，共68.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题12.0分)
计算
(1)(x2−2y)3⋅6xy2x4；
(2)a2−1a2−2a+1⋅2aa2+a．
18. (本小题8.0分)
某工程队承接了3000米的修路任务，在修好600米后，引进了新设备，工作效率是原来的2倍，一共用30天完成了任务．求引进新设备前平均每天修路多少米？
19. (本小题9.0分)
某校高中一年级组建篮球队，对甲、乙两名备选同学进行定位投篮测试，每次投10个球，共投10次．甲、乙两名同学测试情况如图所示：

平均数
众数
方差
甲
7
______
1.2
乙
______
______
2.2
(1)根据图所提供的信息把上表填写完整；
(2)如果你是高一学生会文体委员，会选择哪名同学进入篮球队？请说明理由．

20. (本小题10.0分)
甲、乙两人骑自行车前往A地，他们距A地的路程s(km)与行驶时间t(h)之间的关系如图所示．请根据图象所提供的信息解答下列问题：
(1)甲的速度是______km/h，乙的速度是______km/h；
(2)求出甲或乙距A地的路程s与行驶时间t之间的函数关系式(任求一个)；
(3)直接写出在什么时间段内乙比甲离A地更近？

21. (本小题14.0分)
如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作
AF/​/BC，交BE的延长线于点F，连接CF．
(1)求证：①△AEF≌△DEB；
②四边形ADCF是平行四边形；
(2)若AB=AC，试判断四边形ADCF的形状，并证明你的结论．

22. (本小题15.0分)
如图，在平面直角坐标系中，点A、B、C的坐标分别为(0,2)、(−1,0)、(3,0)，P是直线AB上的一点(与点A、B不重合)，设点P的横坐标为t．
(1)求直线AB的函数表达式；
(2)求满足下列条件时点P的坐标．
①PB=PC；
②△PBC的面积等于12；
(3)设点D与A、B、C点构成平行四边形，直接写出所有符合条件的点D的坐标．


答案和解析

1.【答案】D 
【解析】解：−2xy2x2y=−2yx，
故选：D．
根据分子、分母的公因式是xy，约分即可．
本题考查的是分式的约分，正确确定公因式是解题的关键．

2.【答案】A 
【解析】解：原式=aa−3−3a−3
=a−3a−3
=1．
故选：A．
根据同分母分式的加减法则计算即可．
本题考查同分母分式的加减，解题关键是掌握运算法则．

3.【答案】B 
【解析】
【分析】
绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．本题考查用科学记数法表示较小的数，一般形式为a×10−n，其中1≤|a|<10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．
【解答】
解：0.000056=5.6×10−5．
故选B．  
4.【答案】B 
【解析】解：点P(4,−3)关于y轴对称的点的坐标是：(−4,−3)．
故选：B．
直接利用关于y轴对称点的性质得出答案．关于y轴对称点的性质，纵坐标不变，横坐标互为相反数．
此题主要考查了关于y轴对称点的性质，正确把握横纵坐标的关系是解题关键．

5.【答案】D 
【解析】
【分析】
本题要注意利用一次函数的特点，求出未知数的值从而求得其解析式，求直线y=kx+b(k≠0)平移后的解析式时要注意平移时k的值不变．
根据平移不改变k的值可设y=x+b，然后将点(−2,0)代入即可得出直线的函数解析式．
【解答】
解：设平移后直线的解析式为y=x+b．
把(−2,0)代入直线解析式得0=−2+b，
解得b=2，
所以平移后直线的解析式为y=x+2．
故选D．  
6.【答案】C 
【解析】解：∵点A(−2,a)，B(−1,b)，C(3,c)都在函数y=−6x的图象上，
∴a=−6−2=3，b=−6−1=6，c=−63=−2，
∴c 故选：C．
把点A(−2,a)，B(−1,b)，C(3,c)代入函数y=−6x，求出a、b、c的值，再进行比较即可．
本题考查了反比例函数图象上点的坐标特点，即反比例函数图象上点的坐标一定适合此函数的解析式

7.【答案】B 
【解析】解：根据题意得：小颖该学期总评成绩为90×1+90×3+85×61+3+6=87(分)，
故选：B．
利用加权平均数的定义列式计算即可．
本题主要考查加权平均数，解题的关键是掌握加权平均数的定义．

8.【答案】C 
【解析】解：∵四边形ABCD是平行四边形，
∴∠B=∠D，
∵∠BAC=68°，∠ACB=36°，
∴∠B=180°−68°−36°=76°，
∴∠D=∠B=76°，
故选：C．
由平行四边形的性质得∠B=∠D，再由三角形内角和定理得∠B=76°，即可得出结论．
本题考查了平行四边形的性质以及三角形内角和定理，熟练掌握平行四边形的性质是解题的关键．

9.【答案】D 
【解析】解：如图，∵E是BC的中点，AE⊥BC，
∴AB=AC，
∵四边形ABCD是菱形，
∴AB=BC，AD//BC，
∴AB=BC=AC，∠BAD+∠ABC=180°，
∴△ABC是等边三角形，
∴∠ABC=60°，
∴∠BAD=180°−∠ABC=180°−60°=120°，
故选：D．
先证△ABC是等边三角形，得∠ABC=60°，即可得出结果．
本题考查了菱形的性质、平行线的性质、等腰三角形的判定、等边三角形的判定与性质等知识，熟练掌握菱形的性质，求得∠ABC的度数是解题的关键．

10.【答案】C 
【解析】解：∵正方形ABCD的对角线相交于点O，
∴等腰直角三角形有：△ABC，△BCD，△ACD，△ABD，△OAB，△OBC，△OCD，△OAD，
∴图中共有等腰直角三角形共有8个，
故选：C．
根据正方形的性质及等腰直角三角形的定义即可得到答案．
此题考查了正方形的性质，难度不大，注意不重不漏的数出图中的等腰直角三角形．

11.【答案】B 
【解析】解：∵DE/​/AC，CE/​/BD，
∴四边形ODEC为平行四边形，
∴DE=OC，CE=OD，
∵四边形ABCD为矩形，
∴AC=BD，OD=OC=OA=OB，
∴OD=OC=2，
∴DE=CE=2，
∴四边形OCED的周长为8．
故选：B．
首先利用平行四边形的判定证明四边形ODEC为平行四边形，然后利用矩形的性质得到OD=OC=2即可求出四边形OCED的周长．
本题主要考查了矩形的性质，同时也利用了平行四边形的判定与性质，题目比较简单．

12.【答案】D 
【解析】解：当点P在AB上运动时，AP=x，所以S△APD=12AD⋅AP=12×2x=x(0 当点P在CB上运动时，如图，

所以S△APD=12AD⋅AB=12×2×2=2(2 故选：D．
分类讨论：当点P在AB上运动时，AP=x，根据三角形面积公式得到S△APD=x，自变量x的取值范围为0 本题以动态的形式考查了分类讨论的思想、函数的知识、正方形的性质和三角形的面积公式．注意自变量的取值范围．

13.【答案】x=3 
【解析】解：3x=2x−1，
3(x−1)=2x，
解得：x=3，
检验：当x=3时，x(x−1)≠0，
∴x=3是原方程的根，
故答案为：x=3．
按照解分式方程的步骤，进行计算即可解答．
本题考查了解分式方程，一定要注意解分式方程必须检验．

14.【答案】y=0.3x+6 
【解析】
【分析】
本题考查了根据实际问题列一次函数关系式；得到弹簧总长的等量关系是解决本题的关键．
弹簧总长=挂上xkg的重物时弹簧伸长的长度+弹簧原来的长度，把相关数值代入即可．
【解答】
解：∵每挂1kg重物弹簧伸长0.3cm，
∴挂上x kg的物体后，弹簧伸长0.3x cm，
∴弹簧总长y=0.3x+6．
故答案为y=0.3x+6．  
15.【答案】6 
【解析】解：由题意得：S=|k|=6，则k=±6；
又由于反比例函数图象位于一、三象限，k>0，
则k=6．
故答案为：6．
因为过双曲线上任意一点引x轴、y轴垂线，所得矩形面积S是个定值，即S=|k|，再根据反比例函数的图象所在的象限确定k的值．
本题考查了反比例函数y=kx中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．

16.【答案】菱形 
【解析】
【分析】
根据垂直平分线的画法得出四边形ADBC四边的关系进而得出四边形一定是菱形．
此题主要考查了线段垂直平分线的性质以及菱形的判定，得出四边形四边关系是解决问题的关键．
【解答】
解：∵分别以A和B为圆心，大于12AB的长为半径画弧，两弧相交于C、D，
∴AC=AD=BD=BC，
∴四边形ADBC是菱形．
故答案为菱形．  
17.【答案】解：(1)( x2−2y )3⋅6xy2x4
=x6−8y3⋅6xy2x4
=−3x34y；
(2)a2−1a2−2a+1⋅2 aa2+a
=(a+1)(a−1)(a−1)2⋅2aa(a+1)
=2a−1． 
【解析】(1)原式先计算乘方运算，再计算乘除运算即可得到结果；
(2)先把分式的分子和分母因式分解，再约分即可得到结果．
本题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．

18.【答案】解：设引进新设备前平均每天修路x米．
根据题意，得：600x+3000−6002x=30．
解得：x=60．
经检验：x=60是原方程的解，且符合题意．
答：引进新设备前平均每天修路60米． 
【解析】本题考查分式方程的应用，分析题意，找到关键描述语，得出合适的等量关系是解决问题的关键．设引进新设备前平均每天修路x米，根据“引进新设备前的工作时间+引进新设备后的工作时间=30天”列方程，求解并检验即可求出答案．

19.【答案】6  7  8 
【解析】解：(1)据折线图的数据，甲的数据中，6出现的最多，故众数是6；
乙的数据中，8出现的最多，故众数是8；平均数为110×(4+5+7+6+8+7+8+8+8+9)=7；

平均数
众数
方差
甲
7
6
1.2
乙
7
8
2.2
(2)(答案不唯一，只要说理正确)．
选甲：平均数与乙一样，甲的方差小于乙的方差，甲的成绩较乙的成绩稳定．
选乙：平均数与甲一样，乙投中篮的众数比甲投中篮的众数大，且从折线图看出，乙比甲潜能更大．
(1)根据平均数和众数的定义求解；
(2)根据折线图分析：平均数一样，而乙的众数大，甲的方差小，成绩稳定；故选甲或乙均有道理，只要说理正确即可．
本题考查了平均数、众数、方差的意义与求法及折线图的意义与运用．将统计学知识与实际生活相联系，有利于培养学生学数学、用数学的意识，同时体现了数学来源于生活、应用于生活的本质．

20.【答案】20  30 
【解析】解：(1)从函数图象可知：甲用2.5小时行走了50km；
乙用2小时行走了60km．
所以甲的速度是：502.5=20(km/h)；乙的速度是602=30(km/h)；
故答案为：20，30；
(2)由函数图象知，甲函数过(0,50)、(2.5,0)两点，
设函数关系式为s=at+b，
则有b=502.5a+b=0，
解得：a=−20b=50，
所以所求函数关系式为：s=−20t+50；
同理即可得出乙距A地的路程S与行驶时间t之间的函数关系式为：s=60−30t；
(3)从函数图象可知，在1～2.5小时这段时间内，乙比甲离A地更近．
(1)由图中的时间和路程，可求出速度；
(2)点(0,50)、(2.5,0)在直线上，运用待定系数法即可解答；
(3)t=1时二者相遇，由图可知，在1～2.5小时这段时间内，乙比甲离A地更近．
此题主要考查了一次函数的应用，培养学生从图象上获取信息的能力．

21.【答案】(1)①证明：∵AF/​/BC，
∴∠AFE=∠DBE，∠EAF=∠EDB，
∵点E是AD的中点，
∴AE=DE，
在△AEF和△DEB中，
∠AFE=∠DBE∠EAF=∠EDBAE=DE，
∴△AEF≌△DEB(AAS)，
②证明：∵AD是BC边上的中线，
∴BD=CD，
由①得，△AEF≌△DEB，
∴AF=BD，
∴CD=AF，
∵AF/​/BD，
∴四边形ADCF是平行四边形；
(2)解：四边形ADCF是矩形，理由如下：
∵AB=AC，BD=CD，、
∴AD⊥BC，
∴∠ADC=90°，
∴▱ADCF是矩形． 
【解析】(1)①由AF/​/BC，得∠AFE=∠DBE，∠EAF=∠EDB，结合AE=DE证得结论；
②可得AF=CD，结合AF/​/BC得出结论；
(2)根据等腰三角形“三线合一”可得AD⊥BC，进而得出结论．
本题考查了全等三角形的判定和性质，等腰三角形性质，平行四边形的判定，矩形的判定等知识，解决问题的关键是熟练掌握相关基础知识．

22.【答案】解：(1)设直线AB的函数表达式为y=kx+b(k≠0)，
将A(0,2)，B(−1,0)代入y=kx+b得：b=2−k+b=0，
解得：k=2b=2，
∴直线AB的函数表达式为y=2x+2．
(2)∵点P是直线AB上的一点(与点A、B不重合)，且点P的横坐标为t，
∴点P的坐标为(t,2t+2)．
①∵PB=PC，
∴ [t−(−1)]2+(2t+2−0)2= (t−3)2+(2t+2−0)2，
解得：t=1，
∴点P的坐标为(1,4)．
②∵点B的坐标为(−1,0)，点C的坐标为(3,0)，
∴BC=3−(−1)=4．
∵△PBC的面积等于12，
∴12×4×|2t+2|=12，
解得：t=−4或t=2，
∴点P的坐标为(−4,−6)或(2,6)．
(3)设点D的坐标为(m,n)．
分三种情况考虑：
(i)当AB为对角线时，m+3=−1+0n+0=0+2，
解得：m=−4n=2，
∴点D的坐标为(−4,2)；
(ii)当AC为对角线时，m−1=0+3n+0=2+0，
解得：m=4n=2，
∴点D的坐标为(4,2)；
(iii)当BC为对角线时，m+0=−1+3n+2=0+0，
解得：m=2n=−2，
∴点D的坐标为(2,−2)．
综上所述，点D的坐标为(−4,2)或(4,2)或(2,−2)． 
【解析】(1)根据点A，B的坐标，利用待定系数法即可求出直线AB的函数表达式；
(2)由点P的横坐标，可得出点P的坐标为(t,2t+2)．
①由PB=PC，利用两点间的距离公式(勾股定理)，即可得出关于t的方程，解之即可得出t的值，进而可得出点P的坐标；
②由点B，C的坐标可得出线段BC的长，利用三角形的面积计算公式，结合△PBC的面积等于12，即可得出关于t的方程，解之即可得出t的值，进而可得出点P的坐标；
(3)设点D的坐标为(m,n)，分AB为对角线、AC为对角线及BC为对角线三种情况考虑，利用平行四边形的性质，即可求出m，n的值，进而可得出点D的值．
本题考查了待定系数法求一次函数解析式、两点间的距离公式、三角形的面积、一次函数图象上点的坐标特征以及平行四边形的性质，解题的关键是：(1)根据给定点的坐标，利用待定系数法求出直线AB的函数表达式；(2)①利用两点间的距离公式，找出关于t的方程；②利用三角形的面积计算公式，找出关于t的方程；(3)分AB为对角线、AC为对角线及BC为对角线三种情况，求出点D的坐标．