

2023年湖南省怀化市中考数学三模试卷(含解析)
展开2023年湖南省怀化市中考数学三模试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
1. 12023的相反数是( )
A. 2023 B. −2023 C. 12023 D. −12023
2. 对称美是和谐平衡思想的体现,常被运用于建筑、器物、绘画、标识等作品的设计上,下列大学的校徽图案是轴对称图形的是( )
A. B. C. D.
3. 《2022年国务院政府工作报告》回顾了2021年取得的成就,工作回顾中提到“十四五”实现良好开局,人民生活水平稳步提高,脱贫攻坚成果得到巩固和拓展,新开工改造城镇老旧小区5.6万个,惠及近千万家庭.这个数5.6万用科学记数法表示为(数据来源百度百科《2022年国务院政府工作报告》).( )
A. 5.6×103 B. 0.56×104 C. 5.6×104 D. 56.0×103
4. 下列计算正确的是( )
A. x3−x=x2 B. (−2x2)3=−6x5
C. (x+2)2=x2+4 D. (2x2y)÷(2xy)=x
5. 以下调查中,最适合采用抽样调查的是( )
A. 了解全国中学生的视力和用眼卫生情况
B. 了解全班50名同学每天体育锻炼的时间
C. 学校招聘教师,对应聘人员进行面试
D. 为保证飞机正常飞行,对其零部件进行检查
6. 如图,直线a//b,∠1=35°,∠2=90°,则∠3的大小是( )
A. 25°
B. 35°
C. 45°
D. 55°
7. 如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形ABCD,其中一张纸条在转动过程中,下列结论一定成立的是( )
A. 四边形ABCD周长不变 B. AD=CD
C. 四边形ABCD面积不变 D. AD=BC
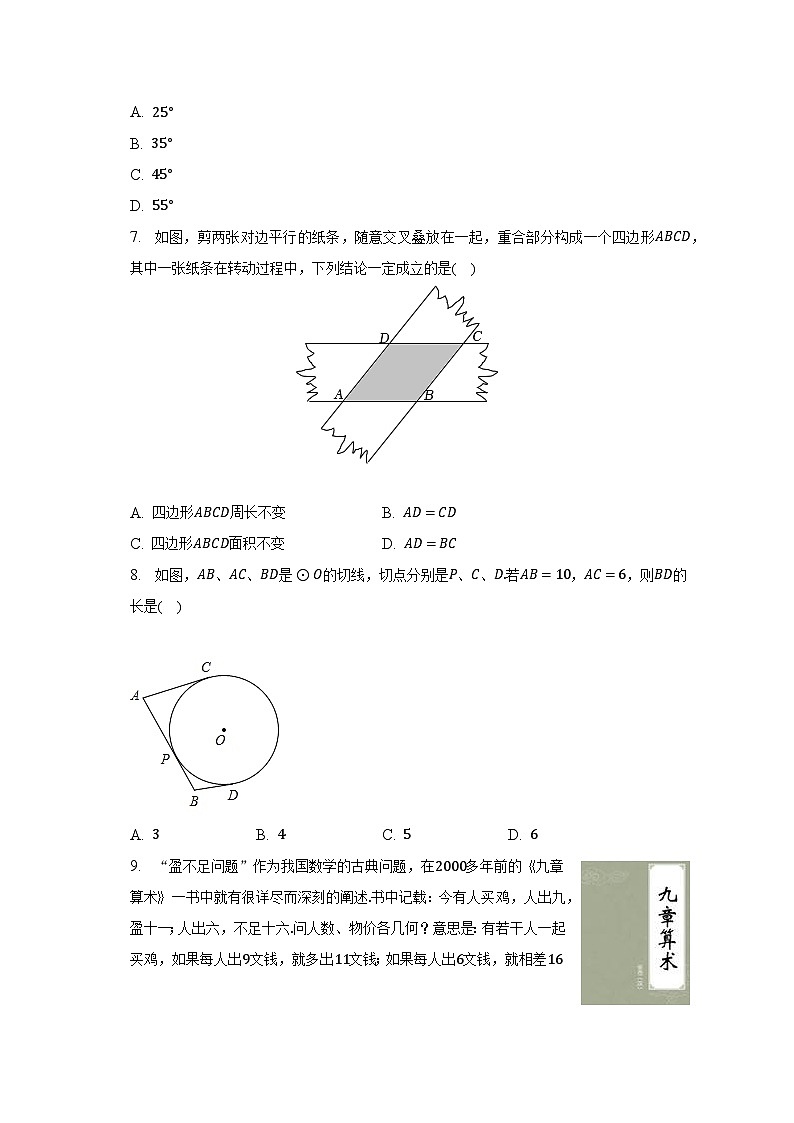
8. 如图,AB、AC、BD是⊙O的切线,切点分别是P、C、D.若AB=10,AC=6,则BD的长是( )
A. 3 B. 4 C. 5 D. 6
9. “盈不足问题”作为我国数学的古典问题,在2000多年前的《九章算术》一书中就有很详尽而深刻的阐述.书中记载:今有人买鸡,人出九,盈十一;人出六,不足十六.问人数、物价各几何?意思是:有若干人一起买鸡,如果每人出9文钱,就多出11文钱;如果每人出6文钱,就相差16文钱.买鸡的人数、鸡的价钱各是多少?若设鸡的价钱是x文钱,根据题意列一元一次方程正确的是( )
A. x−119=x+166 B. x+119=x−166
C. x−116=x+169 D. x−169=x+116
10. 函数y=|ax2+bx+c|(a>0,b2−4ac>0)Noe的图象是由函数y=ax2+bx+c(a>0,b2−4ac>0)的图象x轴上方部分不变,下方部分沿x轴向上翻折而成,如图所示,则下列结论正确的是( )
①2a+b=0;
②4a−2b+c>0;
③c=3;
④将图象向上平移1个单位后与直线y=5有3个交点.
A. ①② B. ①③④ C. ①②④ D. ①②③④
二、填空题(本大题共6小题,共24.0分)
11. 单项式−2a2b3的系数是______ .
12. 分解因式:m3−16m=______.
13. 已知x=2y=3是二元一次方程2x−ky=−5的一个解,那么k的值是______.
14. 一块圆形玻璃镜面碎成了几块,其中一块如图所示,测得弦AB长20厘米,弓形高CD为2厘米,则镜面半径为______厘米.
15. 近年来,洞庭湖区环境保护效果显著,南迁的候鸟种群越来越多.为了解南迁到该区域某湿地的A种候鸟的情况,从中捕捉40只,戴上识别卡并放回;经过一段时间后观察发现,200只A种候鸟中有8只佩有识别卡,由此估计该湿地约有______ 只A种候鸟.
16. 刘徽是我国魏晋时期伟大的数学家,他在《九章算术注》中指出:“勾、股幂合为弦幂,明矣.”也就是说,图1中直角三角形的三边a、b、c存在的关系.他在书中构造了一些基本图形来解决问题.如图2,分别将以a为边长的正方形和b为边长的正方形置于以c为边长的大正方形的左下角和右上角,则图中阴影部分面积等于______ (用含字母a的代数式表示);若(c−a)(c−b)=18,则a+b−c= ______ .
三、解答题(本大题共9小题,共86.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题8.0分)
计算:|−5|+(3− 2)0−2tan45°.
18. (本小题8.0分)
先化简,再求值:(x−yx−x−3yx−y)÷x+yx−y,其中x=1,y=100.
19. (本小题8.0分)
如图所示,工人赵师傅用10块高度都是1.5m的相同长方体新型建筑材料,垒了两堵与地面垂直的墙AB、CD和EF、GH,点P在BE上,已知AP=PF,∠APF=90°.
(1)求证:△ABP≌△PEF;
(2)求BE的长.
20. (本小题9.0分)
我国的教育方针是:教育必须为社会主义现代化建设服务,为人民服务,与生产劳动和社会实践相结合,培养德智体美劳全面发展的社会主义建设者和接班人.为培养德智体美劳全面发展的优秀人才,丰都某中学开展了一系列精品课程,其中有一门课程《研学旅行》开展以来引起广泛关注,九年级2班数学兴趣小组对本班同学对《研学旅行》课的喜欢程度进行了调查,根据收集的数据绘制了两幅不完整的统计图,请根据图中信息,解答下列问题:
(1)九年级2班共有学生 名;
(2)九年级共有学生1200人,根据上述调查结果,估计九年级学生选择D类的大约有多少人?
(3)该校德育处决定从九年级二班调查的A类的4人中,抽2人到八年级开展研学宣讲,若在调查的A类4人中,刚好有2名男生2名女生,用画树状图或列表的方法求抽到的一男一女的概率.
21. (本小题9.0分)
如图,在△ABC中,点D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.
(1)求证:四边形DEFB是平行四边形;
(2)若∠ACB=90°,AC=8cm,DE=3cm,求四边形DEFB的面积.
22. (本小题10.0分)
在平面直角坐标系xOy中,直线l1:y=k1x+b过A(0,−3),B(5,2),直线l2:y=k2x+2.
(1)求直线l1的表达式;
(2)过动点P(0,t)且垂直于y轴的直线与l1,l2的交点分别是C,D.当t≤1时,点C位于点D右方,直接写出k2的取值范围.
23. (本小题10.0分)
某班在庆祝中国共产主义青年团成立100周年活动中,给学生发放笔记本和钢笔作为纪念品.已知每本笔记本比每支钢笔多2元,用240元购买的笔记本数量与用200元购买的钢笔数量相同.
(1)笔记本和钢笔的单价各多少元?
(2)若给全班50名学生每人发放一本笔记本或一支钢笔作为本次活动的纪念品,要使购买纪念品的总费用不超过540元,最多可以购买多少本笔记本?
24. (本小题12.0分)
如图,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2 3.过点D作DF//BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE= 7,求图中阴影部分的面积.
25. (本小题12.0分)
定义:若一个函数图象上存在横、纵坐标相等的点,则称该点为这个函数图象的“等值点”.例如,点(1,1)是函数y=12x+12的图象的“等值点”.
(1)分别判断函数y=x+2,y=x2−x的图象上是否存在“等值点”?如果存在,求出“等值点”的坐标;如果不存在,说明理由;
(2)设函数y=3x(x>0),y=−x+b的图象的“等值点”分别为点A,B,过点B作BC⊥x轴,垂足为C.当△ABC的面积为3时,求b的值;
(3)若函数y=x2−2(x≥m)的图象记为W1,将其沿直线x=m翻折后的图象记为W2.当W1,W2两部分组成的图象上恰有2个“等值点”时,直接写出m的取值范围.
答案和解析
1.【答案】D
【解析】解:由题意可得,12023的相反数是−12023,
故选:D.
根据相反数定义直接求值即可得到答案.
本题考查相反数定义:只有符号不同的两个数叫互为相反数.
2.【答案】B
【解析】解:A,C,D选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
B选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
3.【答案】C
【解析】解:5.6万=56000=5.6×104.
故选:C.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数,当原数绝对值<1时,n是负整数.
此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.【答案】D
【解析】解:A、x3与−x不能合并,故A不符合题意;
B、(−2x2)3=−8x6,故B不符合题意;
C、(x+2)2=x2+4x+4,故C不符合题意;
D、(2x2y)÷(2xy)=x,故D符合题意;
故选:D.
根据合并同类项,幂的乘方与积的乘方,完全平方公式,单项式除以单项式的法则,进行计算逐一判断即可解答.
本题考查了整式的混合运算,准确熟练地进行计算是解题的关键.
5.【答案】A
【解析】解:A、了解全国中学生的视力和用眼卫生情况,最适合采用抽样调查,故A符合题意;
B、了解全班50名同学每天体育锻炼的时间,最适合采用全面调查,故B不符合题意;
C、学校招聘教师,对应聘人员进行面试,最适合采用全面调查,故C不符合题意;
D、为保证飞机正常飞行,对其零部件进行检查,最适合采用全面调查,故D不符合题意;
故选:A.
根据全面调查与抽样调查的特点,逐一判断即可解答.
本题考查了全面调查与抽样调查,熟练掌握全面调查与抽样调查的特点是解题的关键.
6.【答案】D
【解析】解:反向延长∠2的一边,如图,
∵a//b,
∴∠4=∠1=35°,
∵∠2=90°,
∴∠4+∠3=90°,
∴∠3=90°−∠4=55°,
故选:D.
根据平行线的性质以及三角形外角的性质即可得到∠3的度数.
本题考查平行线的性质、三角形外角的性质等知识,解题的关键是灵活运用所学知识解决问题.
7.【答案】D
【解析】解:由题意可知:AB//CD,AD//BC,
∴四边形ABCD为平行四边形,
∴AD=BC,
故选:D.
由条件可知AB//CD,AD//BC,可证明四边形ABCD为平行四边形,可得到AD=BC.
本题主要考查平行四边形的判定和性质;证明四边形ABCD为平行四边形是解题的关键.
8.【答案】B
【解析】解:∵AC、AP为⊙O的切线,
∴AC=AP=6,
∵BP、BD为⊙O的切线,
∴BP=BD,
∴BD=PB=AB−AP=10−6=4.
故选:B.
由于AB、AC、BD是⊙O的切线,则AC=AP,BP=BD,求出BP的长即可求出BD的长.
本题考查了切线长定理,两次运用切线长定理并利用等式的性质是解题的关键.
9.【答案】B
【解析】解:设鸡的价钱是x文钱,根据题意得,
x+119=x−166.
故选:B.
利用人数不变,结合“如果每人出9文钱,多出11文钱;如果每人出6文钱,还差16文钱”,即可得出关于x的一元一次方程.
本题考查了由实际问题抽象出一元一次方程,找准等量关系,正确列出一元一次方程是解题的关键.
10.【答案】C
【解析】解:∵由图象可知二次函数与x轴的交点为(−1,0)和(3,0),
∴二次函数的对称轴为x=−1+32=1,
∴−b2a=1,
∴2a+b=0,故①正确;
由图象可知x=−2时,y>0,
∴4a−2b+c>0,故②正确;
∵由图象可知二次函数y=|ax2+bx+c|与y轴的交点为(0,3),
∴二次函数y=ax2+bx+c与y轴的交点为(0,−3),
∴c=−3,故③错误;
∵将点(−1,0)和(3,0)代入y=ax2+bx−3,
∴a−b−3=09a+3b−3=0,解得a=1b=−2,
∴二次函数的表达式为:y=x2−2x−3,
∵当x=1时,y=1−2−3=−4,
∴图象上当−1
∴此时,直线y=5与函数图象有3个交点,故④正确,
综上:正确的有①②④,
故选:C.
根据图象判断出对称轴的位置,再利用二次函数的对称轴公式,即可得到2a+b=0,故①正确;由图象可知x=−2时,y=4a−2b+c>0,故②正确;由图象可判断二次函数y=ax2+bx+c与y轴的交点为(0,−3),即c=−3,故③错误;求出原二次函数的表达式y=x2−2x−3,即可判断函数顶点的坐标,可以得到将图象向上平移1个单位后,函数顶点的坐标为(1,5),继而得出直线y=5与平移后的函数图象有3个交点,故④正确.
本题考查了二次函数的图象和系数的关系,二次函数图象上点的坐标特征,待定系数法求二次函数的表达式,数形结合是解答本题的关键.
11.【答案】−2
【解析】解:单项式−2a2b3的系数是−2.
故答案为:−2.
根据单项式的系数定义得出答案即可.
本题考查了单项式,能熟记单项式的系数定义是解此题的关键,注意:单项式中的数字因数叫单项式的系数.
12.【答案】m(m+4)(m−4)
【解析】解:m3−16m
=m(m2−16)
=m(m+4)(m−4).
故答案为:m(m+4)(m−4).
先提公因式,再利用平方差公式继续分解即可解答.
本题考查了提公因式法与公式法的综合运用,一定要注意如果多项式的各项含有公因式,必须先提公因式.
13.【答案】3
【解析】解:把x=2y=3代入方程2x−ky=−5得:4−3k=−5,
解得:k=3,
故答案为:3.
把x=2y=3代入方程2x−ky=−5得出4−3k=−5,再求出方程的解即可.
本题考查了二元一次方程的解和解一元一次方程,能得出关于k的一元一次方程是解此题的关键.
14.【答案】26
【解析】解:如图,点O是圆形玻璃镜面的圆心,连接OC,则点C,点D,点O三点共线,
由题意可得:OC⊥AB,AC=12AB=10(厘米),
设镜面半径为x厘米,
由题意可得:x2=102+(x−2)2,
∴x=26,
∴镜面半径为26厘米,
故答案为:26.
根据题意,弦AB长20厘米,弓形高CD为2厘米,根据勾股定理和垂径定理可以求得圆的半径.
本题考查了垂径定理和勾股定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,由勾股定理可求解.
15.【答案】1000
【解析】解:设该湿地约有x只A种候鸟,
则200:8=x:40,
解得x=1000.
故答案为:1000.
在样本中“200只A种候鸟中有8只佩有识别卡”,即可求得有识别卡的所占比例,而这一比例也适用于整体,据此即可解答.
本题考查的是通过样本去估计总体,只需将样本“成比例地放大”为总体即可.
16.【答案】a2 6
【解析】解:图中阴影部分面积等于c2−b2=a2+b2−b2=a2,
如图所示:
AB=c−b,AC=c−a,DE=a−(c−b)=a+b−c,
∵(c−a)(c−b)=c2−bc−ca+ab=18,
∴AB⋅AC=18,即S矩形ACDB=18,
∵S阴影=2S矩形ACDB+a2−(a+b−c)2=a2,
∴(a+b−c)2=36,
∵a+b>c,即a+b−c>0,
∴a+b−c=6,
故答案为:a2,6.
根据阴影面积等于边长为c的正方形面积减去边长为b的正方形面积即可表示;先求出AB=c−b,AC=c−a,DE=a+b−c,再根据(c−a)(c−b)=18得到S矩形ACDB=18,再根据S阴影=2S矩形ACDB+a2−(a+b−c)2=a2,即可求出a+b−c=6.
本题主要考查了因式分解的应用,多项式乘多项式,勾股定理,三角形三边的关系,求平方根,正确理解题意推出(a+b−c)2=36是解题的关键.
17.【答案】解:|−5|+(3− 2)0−2tan45°
=5+1−2×1
=5+1−2
=4.
【解析】首先计算零指数幂、特殊角的三角函数值和绝对值,然后计算乘法,最后从左向右依次计算,求出算式的值即可.
此题主要考查了实数的运算,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.
18.【答案】解:(x−yx−x−3yx−y)÷x+yx−y
=x2−2xy+y2−x2+3xyx(x−y)⋅x−yx+y
=y(x+y)x(x−y)⋅x−yx+y
=yx,
当x=1,y=100时,
原式=100.
【解析】利用分式的相应的法则对式子进行化简,再代入相应的值运算即可.
本题主要考查分式的化简求值,解答的关键是对相应的运算法则的掌握.
19.【答案】(1)证明:∵∠ABP=∠FEP=90°,∠APF=90°,
∴∠APB+∠FPE=∠PFE+∠FPE=90°
∴∠APB=∠PFE(同角的余角相等).
在△ABP与△PEF中,
∠ABP=∠PEF∠APB=∠PFEAP=PF,
∴△ABP≌△PEF(AAS);
(2)由题意知,AB=1.5×3=4.5(m),EF=7×1.5=10.5(m).
由(1)知,△ABP≌△PEF,
∴BP=EF=10.5m,AB=PE=4.5m,
∴BE=BP+PE=15m.
【解析】(1)根据全等三角形的判定定理AAS证得结论;
(2)利用(1)中全等三角形的对应边相等得到:BP=EF=10.5m,AB=PE=4.5m,则BE=BP+PE.
本题主要考查了全等三角形的应用,全等的性质和判定往往是综合在一起应用的,这需要认真分析题目的已知和求证,分清问题中已知的线段和角与所证明的线段或角之间的联系.
20.【答案】40
【解析】解:(1)九年级2班共有学生:4÷10%=40(名),
故答案为:40;
(2)1200×640=180(人),
答:估计九年级学生选择D类的大约有180人;
(3)画树状图如下:
共有12种等可能的结果,其中抽到的一男一女的结果有8种,
∴抽到的一男一女的概率为812=23.
(1)由A类的人数除以所占的百分比得出九年级2班的人数,即可解决问题;
(2)由九年级共有学生人数乘以D类人数所占的比例即可;
(3)画树状图,共有12种等可能的结果,其中抽到的一男一女的结果有8种,再由概率公式求解即可.
本题考查的是用树状图法求概率以及条形统计图和扇形统计图等知识.树状图法可以不重复不遗漏的列出所有可能的结果,适合两步或两步以上完成的事件;解题时要注意此题是放回试验还是不放回试验.用到的知识点为:概率=所求情况数与总情况数之比.
21.【答案】(1)证明:∵点D,E分别是AC,AB的中点,
∴DE是△ABC的中位线,
∴DE//BC,BC=2DE,
∵CF=3BF,
∴BC=2BF,
∴DE=BF,
∴四边形DEFB是平行四边形;
(2)解:由(1)得:DE=BF=3cm,
∵D是AC的中点,AC=8cm,
∴CD=12AC=4cm,
∵∠ACB=90°,
∴四边形DEFB的面积=BF⋅CD=3×4=12(cm2).
【解析】(1)证DE是△ABC的中位线,得DE//BC,BC=2DE,再证DE=BF,即可得出四边形DEFB是平行四边形;
(2)由(1)得:BF=DE=3cm,四边形DEFB是平行四边形,得其面积=BF⋅CD,即可求解.
本题考查了平行四边形的判定与性质、三角形中位线定理、四边形的面积等知识;熟练掌握三角形中位线定理,证明四边形DEFB为平行四边形是解题的关键.
22.【答案】解:(1)∵直线l1:y=k1x+b过A(0,−3),B(5,2),
∴b=−35k1+b=2,解得:k1=1b=−3,
∴直线l1:y=x−3;
(2)∵y=k2x+2,
∴直线l2必过点(0,2),
∵过动点P(0,t)且垂直于y轴的直线与l1,l2的交点分别是C,D,当t≤1时,点C位于点D右方,
①当k2<0时,当t≤1时,必然存在点D位于点C右方,不符合题意;
②当k2>0时,l1,l2平行时,满足题意,此时:k2=1;
l1,l2相交时,则交点的横坐标恒大于5,此时:0
综上:k2的取值范围为0
(2)分k2<0和k2>0,两种情况分类讨论,利用数形结合的思想进行求解即可.
本题考查一次函数的综合应用.正确的求出函数解析式,利用数形结合的思想的进行求解,是解题的关键.
23.【答案】解:(1)设每支钢笔x元,依题意得:
240x+2=200x,
解得:x=10,
经检验:x=10是原方程的解,
故笔记本的单价为:10+2=12(元),
答:笔记本每本12元,钢笔每支10元;
(2)设购买y本笔记本,则购买钢笔(50−y)支,依题意得:
12y+10(50−y)≤540,
解得:y≤20,
故最多购买笔记本20本.
【解析】(1)可设每支钢笔x元,则每本笔记本(x+2)元,根据其数量相同,可列得方程,解方程即可;
(2)可设购买y本笔记本,则购买钢笔(50−y)支,根据总费用不超过540元,可列一元一次不等式,解不等式即可.
本题主要考查一元一次不等式的应用,分式方程的应用,解答的关键是理解清楚题意,找到等量关系和不等关系.
24.【答案】证明:(1)连结OD,
∵AD平分∠BAC交⊙O于D,
∴∠BAD=∠CAD,
∴BD=CD,
∴OD⊥BC,
∵BC//DF,
∴OD⊥DF,
∴DF为⊙O的切线;
(2)连结OB,连结OD交BC于P,作BH⊥DF于H,
∵∠BAC=60°,AD平分∠BAC,
∴∠BAD=30°,
∴∠BOD=2∠BAD=60°,
∴△OBD为等边三角形,
∴∠ODB=60°,OB=BD=2 3,
∴∠BDF=30°,
∵BC//DF,
∴∠DBP=30°,
在Rt△DBP中,PD=12BD= 3,PB= 3PD=3,
在Rt△DEP中,∵PD= 3,DE= 7,
∴PE= ( 7)2−( 3)2=2,
∵OP⊥BC,
∴BP=CP=3,
∴CE=3−2=1,
∵∠DBE=∠CAE,∠BED=∠AEC,
∴△BDE∽△ACE,
∴AE:BE=CE:DE,即AE:5=1: 7,
∴AE=5 77
∵BE//DF,
∴△ABE∽△AFD,
∴BEDF=AEAD,即5DF=5 7712 57,
解得DF=12,
在Rt△BDH中,BH=12BD= 3,
∴阴影部分的面积=△BDF的面积−弓形BD的面积
=△BDF的面积−(扇形BOD的面积−△BOD的面积)
=12⋅12⋅ 3−60π×(2 3)2360+ 34×(2 3)2
=9 3−2π.
【解析】(1)连结OD,根据垂径定理得到OD⊥BC,根据平行线的性质得到OD⊥DF,根据切线的判定定理证明;
(2)连结OB,连结OD交BC于P,作BH⊥DF于H,证明△OBD为等边三角形,得到∠ODB=60°,OB=BD=2 3,根据勾股定理求出PE,证明△ABE∽△AFD,根据相似三角形的性质求出AE,根据阴影部分的面积=△BDF的面积−弓形BD的面积计算.
本题考查的是切线的判定,扇形面积计算,相似三角形的判定和性质,圆周角定理的应用,等边三角形的判定和性质,掌握切线的判定定理,扇形面积公式是解题的关键.
25.【答案】解:(1)在y=x+2中,令x=x+2,得0=2不成立,
∴函数y=x+2的图象上不存在“等值点”;
在y=x2−x中,令x2−x=x,
解得:x1=0,x2=2,
∴函数y=x2−x的图象上有两个“等值点”(0,0)或(2,2);
(2)在函数y=3x(x>0)中,令x=3x,
解得:x= 3,
∴A( 3, 3),
在函数y=−x+b中,令x=−x+b,
解得:x=12b,
∴B(12b,12b),
∵BC⊥x轴,
∴C(12b,0),
∴BC=12|b|,
∵△ABC的面积为3,
∴12×12|b|×| 3−12b|=3,
当b<0时,b2−2 3b−24=0,
解得b=−2 3,
当0≤b<2 3时,b2−2 3b+24=0,
∵Δ=(−2 3)2−4×1×24=−84<0,
∴方程b2−2 3b+24=0没有实数根,
当b≥2 3时,b2−2 3b−24=0,
解得:b=4 3,
综上所述,b的值为−2 3或4 3;
(3)令x=x2−2,
解得:x1=−1,x2=2,
∴函数y=x2−2的图象上有两个“等值点”(−1,−1)或(2,2),
①当m<−1时,W1,W2两部分组成的图象上必有2个“等值点”(−1,−1)或(2,2),
W1:y=x2−2(x≥m),
W2:y=(x−2m)2−2(x
整理得:x2−(4m+1)x+4m2−2=0,
∵W2的图象上不存在“等值点”,
∴Δ<0,
∴(4m+1)2−4(4m2−2)<0,
∴m<−98,
②当m=−1时,有3个“等值点”(−2,−2)、(−1,−1)、(2,2),
③当−1
⑤当m>2时,W1,W2两部分组成的图象上没有“等值点”,
综上所述,当W1,W2两部分组成的图象上恰有2个“等值点”时,m<−98或−1
(1)根据“等值点”的定义建立方程求解即可得出答案;
(2)先根据“等值点”的定义求出函数y=3x(x>0)的图象上“等值点”A( 3, 3),同理求出B(12b,12b),根据△ABC的面积为3可得12×12|b|×| 3−12b|=3,求解即可;
(3)先求出函数y=x2−2的图象上有两个“等值点”(−1,−1)或(2,2),再利用翻折的性质分类讨论即可.
【高频真题解析】湖南省怀化市中考数学二模试题(含详解): 这是一份【高频真题解析】湖南省怀化市中考数学二模试题(含详解),共26页。试卷主要包含了如图个三角形.,如图,,如图,A等内容,欢迎下载使用。
2023年湖南省怀化市中考数学二模试卷(含解析): 这是一份2023年湖南省怀化市中考数学二模试卷(含解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年湖南省怀化市中考数学试卷(含解析): 这是一份2023年湖南省怀化市中考数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












