
2022-2023学年云南省昆明市五华区八年级(下)期末数学试卷(含解析)
展开2022-2023学年云南省昆明市五华区八年级(下)期末数学试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
1. 如果 a−3有意义,则a的取值范围是( )
A. a>3 B. a<3 C. a≥3 D. a≤3
2. 下列各组数中能作为直角三角形的三边长的是( )
A. 1,2,3 B. 1,1, 3 C. 13,14,15 D. 6,8,10
3. 如图所示,数学活动课上,某兴趣小组要测量池塘两端A,B的距离,他们先在平地上取一个点C,从点C不经过池塘可以直接到达点A和点B,连接AC,BC,并分别找出AC,BC的中点D,E,连接DE.并量出DE=24m,则A,B的距离为( )
A. 48m B. 60m C. 80m D. 不能确定
4. 《义务教育课程标准(2022年版)》首次把学生学会烹饪纳入劳动教育课程,并作出明确规定某班有七名同学已经学会烹饪的菜品种数依次为:3,5,4,6,3,3,4,则这组数据的众数、中位数和平均数分别是( )
A. 3,4,4 B. 4,3,4 C. 3,3,4 D. 4,4,3
5. 下列关于函数y=13x的结论正确的是( )
A. 函数图象经过点(1,3) B. 函数图象经过第一、三象限
C. y随x的增大而减小 D. 不论x为何值,总有y>0
6. 下列各式中,运算正确的是( )
A. 3 3− 3=3 B. (−2)2=−2 C. 2+ 3=2 3 D. 2× 8=4
7. 在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
A. AB//DC,AD=BC B. AB=DC,AD=BC
C. AO=CO,BO=DO D. AB//DC,AD//BC
8. 矩形具有而一般平行四边形不具有的性质是( )
A. 对角线相等 B. 对边相等 C. 对角相等 D. 对角线互相平分
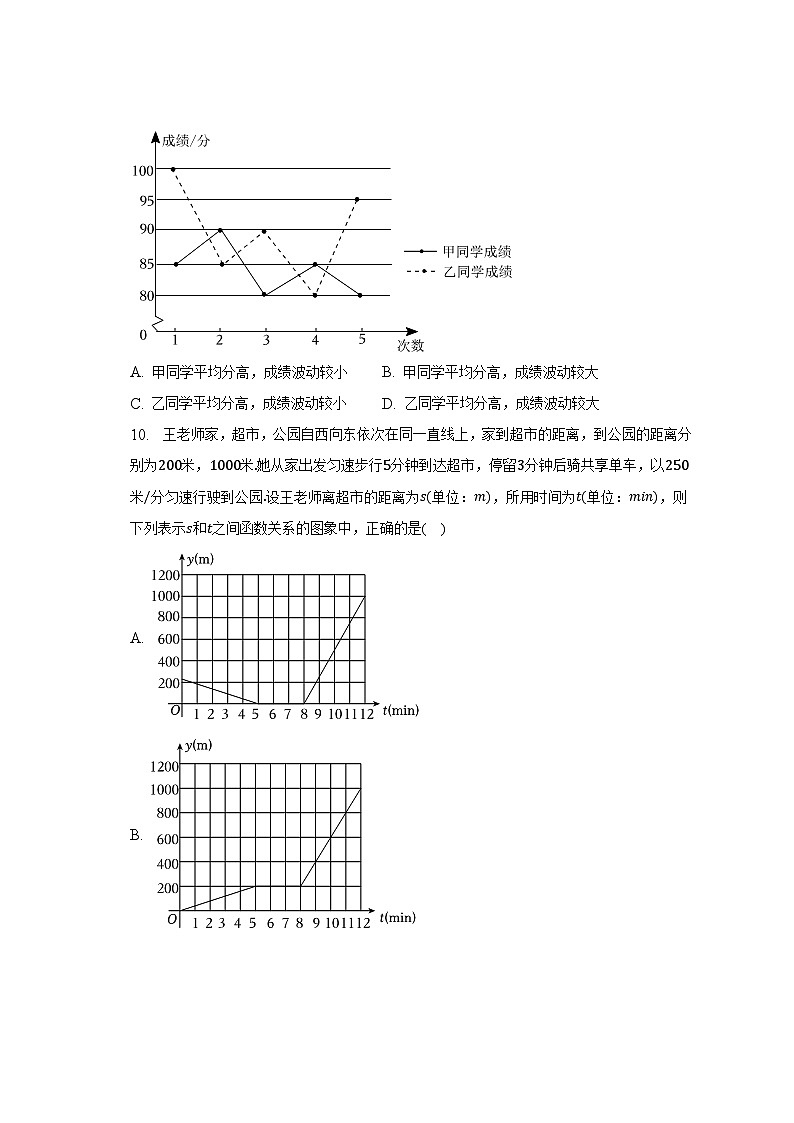
9. 如图是甲、乙两名同学五次数学测试成绩的折线图.比较甲、乙两名同学的成绩,下列说法正确的是( )
A. 甲同学平均分高,成绩波动较小 B. 甲同学平均分高,成绩波动较大
C. 乙同学平均分高,成绩波动较小 D. 乙同学平均分高,成绩波动较大
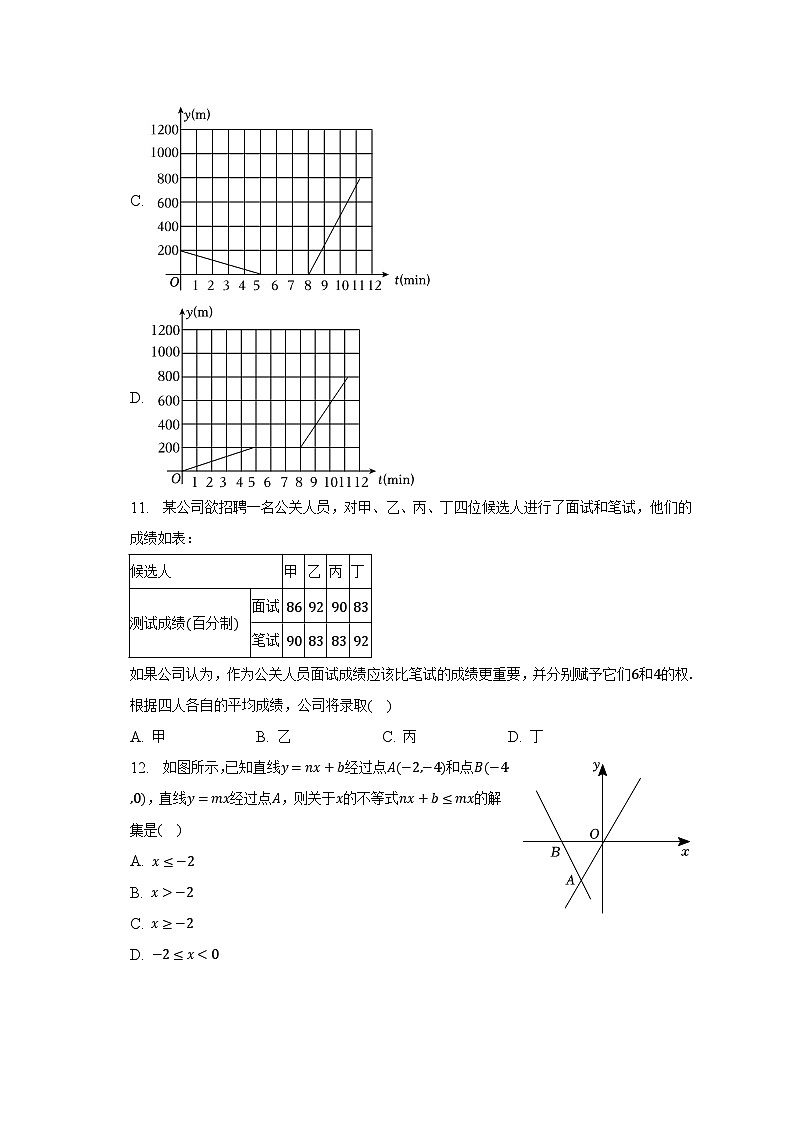
10. 王老师家,超市,公园自西向东依次在同一直线上,家到超市的距离,到公园的距离分别为200米,1000米.她从家出发匀速步行5分钟到达超市,停留3分钟后骑共享单车,以250米/分匀速行驶到公园.设王老师离超市的距离为s(单位:m),所用时间为t(单位:min),则下列表示s和t之间函数关系的图象中,正确的是( )
A.
B.
C.
D.
11. 某公司欲招聘一名公关人员,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人
甲
乙
丙
丁
测试成绩(百分制)
面试
86
92
90
83
笔试
90
83
83
92
如果公司认为,作为公关人员面试成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,公司将录取( )
A. 甲 B. 乙 C. 丙 D. 丁
12. 如图所示,已知直线y=nx+b经过点A(−2,−4)和点B(−4,0),直线y=mx经过点A,则关于x的不等式nx+b≤mx的解集是( )
A. x≤−2
B. x>−2
C. x≥−2
D. −2≤x<0
二、填空题(本大题共4小题,共8.0分)
13. 计算: 18÷ 2=______.
14. 如图,过正方形ABCD的顶点B作直线l,过A、C作l的垂线,垂足分别为E、F.若AE=1,CF=3,则AB的长度为______.
15. 如图所示,在△ABC中,∠C=90°,点D为BC边上一点,将△ACD沿AD翻折得到△AC′D,若点C′在AB边上,AC=6,BC=8,则AD的长为______ .
16. 对于实数a,b,定义符号min{a,b},其意义为:当a≥b时,min{a,b}=b;当a
17. (本小题6.0分)
计算:( 6−3)( 6+3)+( 2−1)2.
18. (本小题6.0分)
在正方形网格中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,如图所示,点A,B,O都在格点上,求∠AOB的度数.
19. (本小题7.0分)
某校开展了安全知识宣传教育活动,为了解这次活动的效果,从该校七、八年级学生中各随机抽取20名学生进行测试,其中抽测的八年级学生成绩如下:
81 83 84 89 86 87 87 88 89 90
92 92 93 95 95 95 99 99 100 100
对七、八年级参加测试学生成绩整理如下:
80≤x<85
85≤x<90
90≤x<95
95≤x≤100
七年级
4
6
2
8
八年级
3
a
4
7
对两组数据分析如下:
平均数
中位数
众数
方差
七年级
91
89
97
40.9
八年级
91
b
95
33.2
根据以上信息,解答下列问题:
(1)填空:a= ______ ,b= ______ ;
(2)样本数据中七年级甲同学和八年级乙同学的分数都是90分,把七、八年级各20名同学的分数按从高到底的顺序排列,______ 同学的成绩在本年级更靠前(填“甲”或“乙”);
(3)如果把成绩在90分以上(含90分)定为优秀,那么该校八年级300名学生中,成绩为优秀的学生约有多少人?
20. (本小题7.0分)
如图,在平行四边形ABCD中,E为线段AD的中点,延长BE与CD的延长线交于点F,连接AF,BD,∠BDF=90°.
(1)求证:四边形ABDF是矩形;
(2)若BC=4,DF=3,求四边形ABCF的面积S.
21. (本小题7.0分)
如图所示,一次函数y=−x+b的图象分别与x,y轴交于A,B两点,点A的坐标为(6,0),过点B的直线交x轴负半轴于点C,且OB:OC=3:1.
(1)求点B的坐标;
(2)求直线BC的解析式;
(3)若点P(m,2)在△ABC的内部,直接写出m的取值范围.
22. (本小题7.0分)
勾股定理是初等几何中最重要的定理之一,它的证明方法很多,如图1是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,通过对图形的切割、拼接,巧妙的利用面积关系证明了勾股定理.
(1)定理证明:
图1是由四个全等的直角三角形围成的一个大正方形,中间的部分是一个小正方形(阴影).如果直角三角形较小的直角边长为a,较大的直角边长为b,斜边长为c,请你根据图1证明勾股定理;
(2)问题解决:
如图2,圆柱的底面半径为40cm,高为30πcm,蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是多少厘米?(结果保留π)
23. (本小题8.0分)
某书店制订了“读书节”活动计划,以下是活动计划的部分信息:
书本类别
A类
B类
进价(单位:元)
18
12
备注
用不超过16800元购进两类图书共1000本,A类图书不少于600本.
(1)陈经理查看计划时发现:A类图书的标价是B类图书的1.5倍,若顾客用540元购买图书,单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A,B两类图书的标价;
(2)为了扩大影响,陈经理调整了销售方案:A类图书售价每本降低4元,B类图书价格不变.此时书店应如何进货才能获得最大利润?
24. (本小题8.0分)
在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE.
(1)如图1,当点E在菱形ABCD内部或边上时,连接CE.则BP与CE的数量关系是______ ,CE与AD的位置关系是______ ;
(2)如图2,当点E在菱形ABCD外部时,连接CE.那么(1)中的结论是否仍成立?若成立,请予以证明;若不成立,请说明理由;
(3)如图3,当点P在线段BD的延长线上时,连接BE,若AB=4 3,BE=4 19,请直接写出四边形ADPE的面积.
答案和解析
1.【答案】C
【解析】解:由题意得,a−3≥0,
解得a≥3.
故选:C.
根据被开方数大于等于0列式计算即可得解.
本题考查的知识点为:二次根式的被开方数是非负数.
2.【答案】D
【解析】解:A、∵12+22≠32,
∴1,2,3不能作为直角三角形边长,
故A不符合题意;
B、∵12+12≠( 3)2,
∴1,1, 3不能作为直角三角形边长,
故B不符合题意;
C、∵132+42≠152,
∴13,14,15不能作为直角三角形边长,
故C不符合题意;
D、∵62+82=102,
∴6,8,10能作为直角三角形边长,
故D符合题意;
故选:D.
根据勾股定理的逆定理,进行计算即可解答.
本题考查了勾股定理的逆定理,熟练掌握勾股定理的逆定理是解题的关键.
3.【答案】A
【解析】解:∵E、D分别是BC、AC中点,
∴DE是△ABC的中位线,
∴DE=12AB,
∵DE=24m,
∴AB=48m.
故选:A.
由E、D分别是BC、AC中点,得到DE是△ABC的中位线,由三角形的中位线定理即可求出AB的长.
本题考查三角形中位线定理,关键是掌握三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
4.【答案】A
【解析】解:∵这7个数据中出现次数最多的数据是3,
∴这组数据的众数是3.
把这组数据按从小到大顺序排列,为
3,3,3,4,4,5,6,
位于中间的数据为4,
∴这组数据的中位数为4,
(3+3+3+4+4+5+6)÷7=4,
∴这组数据的平均数为4.
故选:A.
这7个数据中出现次数最多的数据为众数是3;把这组数据按从小到大的顺序排列后,位于中间的数据是4.
本题主要考查众数的定义:一组数据中出现次数最多的数据就是这组数据的众数,中位数是指将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称中间位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
5.【答案】B
【解析】解:A.当x=1时,y=13×1=13≠3,
∴函数图象不经过点(1,3),选项A不符合题意;
B.∵k=13>0,
∴函数图象经过第一、三象限,选项B符合题意;
C.∵k=13>0,
∴y随x的增大而增大,选项C不符合题意;
D.只有当x>0时,y>0,选项D不符合题意.
故选:B.
利用正比例函数的性质以及图象上点的坐标性质,分别判断得出即可.
本题考查了一次函数图象上点的坐标特征、正比例函数的性质以及一次函数图象与系数的关系,逐一分析各选项的正误是解题的关键.
6.【答案】D
【解析】解:3 3− 3=2 3,故选项A错误,不符合题意;
(−2)2=2,故选项B错误,不符合题意;
2+ 3不能合并,故选项C错误,不符合题意;
2× 8= 16=4,故选项D正确,符合题意;
故选:D.
计算出各个选项中式子的正确结果,即可判断哪个选项符合题意.
本题考查二次根式的混合运算,熟练掌握运算法则是解答本题的关键.
7.【答案】A
【解析】解:A、错误.当AB//DC,AD=BC时,四边形ABCD可能是等腰梯形也可能是平行四边形,故错误.
B、正确.因为两组对边分别相等的四边形是平行四边形.
C、正确.因为对角线互相平分的四边形是平行四边形.
D、正确.因为两组对边分别平行的四边形是平行四边形,
故选A.
根据平行四边形的判定方法一一判断即可.
本题考查平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
8.【答案】A
【解析】解:由于矩形的对角线互相平分且相等,而平行四边形的对角线互相平分,不一定相等,
故矩形具有而一般平行四边形不具有的性质是对角线相等.
故选:A.
由于矩形是特殊的平行四边形,所以矩形具有一般平行四边形的性质;矩形具有对角线相等这个性质,一般的平行四边形不具有,根据选项即可得到本题答案.
本题考查了平行四边形的性质及矩形的性质,侧重考查知识点的理解、应用能力.
9.【答案】D
【解析】解:乙同学的平均分是:15×(100+85+90+80+95)=90,
甲同学的平均分是:15×(85+90+80+85+80)=84,
因此乙的平均数较高;
S乙2=15×[(100−90)2+(85−90)2+(80−90)2+(95−90)2]=50,
S甲2=15×[(85−84)2+(90−84)2+(80−84)2+(80−84)2+(85−84)2]=14,
∵50>14,
∴乙的离散程度较高,不稳定,甲的离散程度较低,比较稳定;
故选:D.
分别求出甲、乙的平均数、方差,比较得出答案.
本题考查平均数、方差的计算方法,从统计图中获取数据,是正确计算的前提.
10.【答案】C
【解析】解:由题意可得,王老师离超市的距离为s(单位:m),所用时间为t(单位:min),家到超市、超市到公园的距离分别为200m,800m,
∵王老师从家出发匀速步行5分钟到达超市,
∴这个过程y随x的增大而减小,
∵王老师到超市后,停留3min,
∴这个过程y随x的变化不改变,y的值都是0,
∵王老师250米/分匀速行驶到公园,
∴这个过程y随x的增大而增大,当x=5+3+800÷250=11.2时,y=800,
故选:C.
根据题意和题目中的数据,可以写出各段y随x的变化如何变化,然后即可判断哪个选项符合题意.
本题考查了函数的图象,利用数形结合思想解决问题是解题的关键.
11.【答案】B
【解析】解:甲的平均成绩为:(86×6+90×4)÷10=87.6(分),
乙的平均成绩为:(92×6+83×4)÷10=88.4(分),
丙的平均成绩为:(90×6+83×4)÷10=87.2(分),
丁的平均成绩为:(83×6+92×4)÷10=86.6(分),
因为乙的平均分数最高,所以乙将被录取.
故选:B.
首先根据权重,可知每个人的成绩可以用(面试成绩×6+笔试成绩×4)÷10进行计算得到;再比较四个人成绩的高低,则成绩最高的人即为公司录取的人,从而解决问题.
本题考查加权平均数,解答本题的关键是明确加权平均数的计算方法,求出甲乙丙丁的成绩.
12.【答案】C
【解析】解:由图象可知,当x≥−2时,直线y=nx+b在直线y=mx下方,
∴关于x的不等式nx+b≤mx的解集是x≥−2,
故选:C.
根据A点的坐标结合图象即可求解.
本题考查了一次函数与一元一次不等式,一次函数的性质,理解图象是本题的关键.
13.【答案】3
【解析】解:原式= 18÷2= 9=3.
故答案为:3.
直接运用二次根式的除法法则进行计算即可.
本题考查了二次根式的除法.
14.【答案】 10
【解析】解:∵四边形ABCD是正方形,
∴∠CBF+∠FBA=90°,AB=BC,
∵CF⊥BE,
∴∠CBF+∠BCF=90°,
∴∠BCF=∠ABE,
∵∠AEB=∠BFC=90°,AB=BC,
∴△ABE≌△BCF(AAS)
∴AE=BF,BE=CF,
∴AB= 1+9= 10.
故答案为: 10.
先利用AAS判定△ABE≌△BCF,从而得出AE=BF,BE=CF,最后得出AB的长.
此题主要考查了正方形的性质及全等三角形的判定方法,做题时要注意各个条件之间的关系并灵活运用.
15.【答案】3 5
【解析】解:由折叠可知:DC=DC′,∠DC′A=∠C=90°,AC′=AC=6,
在Rt△ABC中,由勾股定理得:AB= AC2+BC2=10,
∴BC′=AB−AC′=4,
设BD=x,则CD=DC′=8−x,
在Rt△BDC′中,由勾股定理得:x2=42+(8−x)2,
∴x=5,
∴BD=5,CD=3,
∴AD= AC2+CD2= 62+32=3 5,
故答案为:3 5.
由勾股定理求出AB=10,由折叠的性质得出CD=DC′,∠C=∠AC′D=90°,AC′=AC=6,得出BC′=AB−AC′=4,∠BC′D=90°,设BD=x,则CD=DC′=8−x,在Rt△BDC′中,由勾股定理得出方程,可求BD长,由勾股定理可求AD的长.
本题考查了翻折变换的性质,勾股定理等知识;熟练掌握翻折变换的性质,由勾股定理得出方程是解题的关键.
16.【答案】53
【解析】解:由题意得:
y=2x−1y=−x+3,
解得:x=43y=53,
当2x−1≥−x+3时,x≥43,
∴当x≥43时,y=min{2x−1,−x+3}=−x+3,
由图象可知:此时该函数的最大值为53;
当2x−1≤−x+3时,x≤43,
∴当x≤43时,y=min{2x−1,−x+3}=2x−1,
由图象可知:此时该函数的最大值为53;
综上所述,y=min{2x−1,−x+3}的最大值是当x=43所对应的y的值,
如图所示,当x=43时,y=53,
故答案为:53.
根据定义先列不等式:2x−1≥−x+3和2x−1≤−x+3,确定其y=min{2x−1,−x+3}对应的函数,画图象可知其最大值.
本题考查了新定义问题、一元一次不等式及一次函数的交点问题,认真阅读理解其意义,并利用数形结合的思想解决函数的最值问题.
17.【答案】解:( 6−3)( 6+3)+( 2−1)2
=( 6)2−32+( 2)2−2 2+1
=6−9+2−2 2+1
=−2 2.
【解析】根据二次根式混合运算的法则计算即可.
本题考查了二次根式的混合运算,熟练掌握二次根式混合运算的法则是解题的关键.
18.【答案】解:连接AB,
∵AO=AB= 12+32= 10,OB= 22+42=2 10,
∴AO2+AB2=OB2,
∴∠OAB=90°,
∴△AOB是等腰直角三角形,
∴∠AOB=45°.
【解析】根据勾股定理和勾股定理的逆定理即可得到结论.
本题考查了勾股定理,勾股定理的逆定理,等腰直角三角形判定和性质,熟练掌握勾股定理的逆定理是解题的关键.
19.【答案】6 91 甲
【解析】解:(1)由题意可知,a=6,b=90+922=91,
故答案为:6;91;
(2)因为89<90<91,所以把七八年级这20名同学的分数按从高到低的顺序排列,甲同学的成绩在本年级靠前.
故答案为:甲;
(3)300×1120=165(人),
答:估计八年级优秀等次有165人.
(1)分别对数据进行分析,数出满足条件数的个数,将数据从小到大排列,找到中位数.
(2)根据七八年级学生成绩的中位数进行解答即可.
(3)利用样本估计总体即可.
本题考查频数分布表、用样本估计总体、方差、中位数、众数的意义及求法,理解各个统计量的意义,明确各个统计量的特点是解决问题的前提和关键.
20.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AB//CD,
即AB//DF,
∴∠ABF=∠BFD,∠BAD=∠ADF,
∵E为线段AD的中点,
∴AE=DE,
在△ABE与△DFE中,
∠ABE=∠DFB∠BAD=∠ADFAE=DE,
∴△ABE≌△DFE(AAS),
∴BE=EF,
∴四边形ABCD是平行四边形,
∵∠BDF=90°,
∴四边形ABDF是矩形;
(2)解:四边形ABCD是平行四边形,
∴BC=AD,
∵四边形ABDF是矩形,
∴AD=BF,
∴BC=BF=4,
∵BD⊥CF,
∴CD=DF=3,
∴BD= BC2−CD2= 42−32= 7,
∴四边形ABCF的面积S=△BCD+矩形ABDF=12× 7×3+ 7×3=9 72.
【解析】(1)根据平行四边形的性质得到AB//CD,即AB//DF,根据平行线的性质得到∠ABF=∠BFD,∠BAD=∠ADF,根据全等三角形的性质得到BE=EF,根据矩形的判定定理即可得到结论;
(2)根据平行四边形的性质得到BC=AD,根据矩形的性质得到AD=BF,根据勾股定理得到BD= BC2−CD2= 42−32= 7,根据矩形和三角形的面积公式即可得到结论.
本题考查了矩形的判定和性质,全等三角形的判定和性质,平行四边形的性质,勾股定理,熟练掌握矩形的性质是解题的关键.
21.【答案】解:(1)∵点A(6,0)在一次函数y=−x+b的图象上,
∴−6+b=0,
解得:b=6,
∴直线AB的解析式为y=−x+6,
令x=0得,y=6,
∴B(0,6);
(2)∵B(0,6),
∴OB=6,
∵OB:OC=3:1,
∴OC=2,
∴C(−2,0),
设直线BC的解析式为y=kx+6,
将点C(−2,0)代入得,−2k+6=0,
解得:k=3,
∴直线BC的解析式为y=3x+6;
(3)将y=2代入y=3x+6得,3x+6=2,
解得:x=−43,
将y=2代入y=−x+6得,−x+6=2,
解得:x=4,
如图,
结合图象可知,m的取值范围为−43
(2)由OB:OC=3:1可得C(−2,0),再设直线BC的解析式为y=kx+6,利用待定系数法即可求解;
(3)把y=2分别代入直线AB和BC的解析式中,求出对应的x值,结合函数图象即可确定m的取值范围.
本题主要考查用待定系数法求一次函数解析式,直线与x轴、y轴的交点坐标,确定自变量的取值范围,解题关键是熟练掌握利用待定系数法求函数解析式,并善于运用数形结合思想解决问题.
22.【答案】解:(1)∵阴影部分的面积=大正方形面积−4直角三角形面积,
∴(b−a)2=c2−4×12ab,
∴a2−2ab+b2=c2−2ab,
∴a2+b2=c2;
(2)画出圆柱侧面展开图:
根据圆柱底面半径为40cm,得出AC=2×40π2=40π(cm),
∵高为30πcm,
∴AB= AC2+BC2=50π(cm),
∴从点A爬到点B的最短路程是50π厘米.
【解析】(1)利用阴影部分的面积=大正方形面积−4直角三角形面积额即可得答案;
(2)画出圆柱侧面展开图矩形,利用勾股定理即可得答案.
本题考查勾股定理证明,掌握面积法是解题关键.
23.【答案】(1)设B类图书的标价为x元,则A类图书的标价为1.5x元,
根据题意可得540x−10=5401.5x,
化简得:540−10x=360,
解得:x=18,
经检验:x=18是原分式方程的解,
且符合题意,
则A类图书的标价为:1.5x=1.5×18=27(元),
答:A类图书的标价为27元,B类图书的标价为18元;
(2)设购进A类图书t本,总利润为w元,A类图书的标价为27−4=23元,
由题意得18t+12(1000−t)≤16800t≥600,
解得600≤t≤800,
则总利润w=(23−18)t+(18−12)(1000−t)=5t−6t+6000=−t+6000,
∴当t=600时,总利润最大,
∴此时书店A图书购进600本,B类图书购进400本时,才能获得最大利润.
【解析】(1)先设B类图书的标价为x元,则由题意可知A类图书的标价为1.5x元,然后根据题意列出方程,求解即可;
(2)先设购进A类图书t本,总利润为w元,则购进B类图书为(1000−t)本,根据题目中所给的信息列出不等式组,求出t的取值范围,然后根据总利润w=总售价一总成本,求出最佳的进货方案.
本题考查分式方程和一次函数的应用,根据题意列出分式方程和函数关系式是解题的关键.
24.【答案】BP=CE CE⊥AD
【解析】解:(1)如图1,连接AC,
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,
∴∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∵∠BAC=∠PAE,
∴∠BAP=∠CAE,
在△BAP和△CAE中,
AB=AC∠BAP=∠CAEAP=AE,
∴△BAP≌△CAE(SAS),
∴BP=CE,∠ABP=∠ACE=30°,
延长CE交AD于H,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,
∴CE⊥AD,
故答案为:BP=CE,CE⊥AD;
(2)当点E在菱形ABCD外部时,(1)中的结论还成立,
理由如下:
如图2,连接AC交BD于O,设CE交AD于H,
∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC,△ACD都是等边三角形,∠ABD=∠CBD=30°,
∴AB=AC,∠BAC=60°,
∵△APE是等边三角形,
∴AP=AE,∠PAE=60°,
∵∠BAP=∠CAE,
在△BAP和△CAE中,
AB=AC∠BAP=∠CAEAP=AE,
∴△BAP≌△CAE(SAS),
∴BP=CE,∠ABP=∠ACE=30°,
∵∠CAH=60°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,
∴CE⊥AD;
(3)如图3,连接AC交BD于O,连接CE,作EH⊥AP于H,
∵四边形ABCD是菱形,
∴AC⊥BD,BD平分∠ABC,
∴∠ABO=30°,
∵AB=4 3,
∴AO=2 3,
∴BO=DO= 3AO=6,
∴BD=12,
由(2)知CE⊥AD,
∵AD//BC,
∴CE⊥BC,
∵BE=4 19,BC=AB=4 3,
∴CE= BE2−BC2= (4 19)2−(4 3)2=16,
∴由(2)知BP=CE=16,
∴DP=BP−BD=16−12=4,
∴OP=10,
∴AP= AO2+OP2= (2 3)2+102=4 7,
∵△APE是等边三角形,
∴AH=12AP=2 7,AE=AP=EP=4 7,
∴EH= 3AH=2 21,
∵S四边形ADPE=S△ADP+S△APE,
∴S四边形ADPE=12DP⋅AO+12AP⋅EH=12×4×2 3+12×4 7×2 21=4 3+28 3=32 3,
∴四边形ADPE的面积是32 3.
(1)连接AC,根据SAS证△BAP≌△CAE,即可得出BP=CE,延长CE交AD于H,再根据∠CAH+∠ACH=90°得出CE⊥AD;
(2)连接AC交BD于O,设CE交AD于H,根据SAS证△BAP≌△CAE,即可得出BP=CE,再根据∠CAH+∠ACH=90°得出CE⊥AD;
(3)连接AC交BD于O,连接CE,作EH⊥AP于H,利用勾股定理分别求出OA,OP,AP,EH的长度,再根据S四边形ADPE=S△ADP+S△APE,即可求出四边形的面积.
本题是四边形综合题,考查菱形的性质,等边三角形的性质,全等三角形的判定和性质等知识,添加恰当辅助线构造全等三角形是解题的关键.
2023-2024学年云南省昆明市五华区九年级(上)期末数学试卷(含解析): 这是一份2023-2024学年云南省昆明市五华区九年级(上)期末数学试卷(含解析),共16页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年云南省昆明市五华区七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年云南省昆明市五华区七年级(下)期末数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年云南省昆明市五华区七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年云南省昆明市五华区七年级(下)期末数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












