第10讲 从函数观点看一元二次方程和一元二次不等式-新高一数学暑假精品课（苏教版必修第一册）

这是一份第10讲 从函数观点看一元二次方程和一元二次不等式-新高一数学暑假精品课（苏教版必修第一册），文件包含第10讲从函数观点看一元二次方程和一元二次不等式解析版docx、第10讲从函数观点看一元二次方程和一元二次不等式原卷版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
第10讲 从函数观点看一元二次方程和一元二次不等式

1．会结合一元二次函数的图象，判断一元二次方程实根的存在性及实根的个数．
2．了解函数的零点与方程根的关系．
3．经历从实际情境中抽象出一元二次不等式的过程，了解一元二次不等式的现实意义．能借助一元二次函数求解一元二次不等式，并能用集合表示一元二次不等式的解集．　
4．借助一元二次函数的图象，了解一元二次不等式与相应函数、方程的联系．

知识点一 二次函数的零点
1．一般地，一元二次方程ax2＋bx＋c＝0(a≠0)的根就是二次函数y＝ax2＋bx＋c(a≠0)当函数值取时自变量x的值，即二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴交点的横坐标，也称为二次函数y＝ax2＋bx＋c(a≠0)的零点．
2．函数的零点不是点，而是一个实数，是函数的图象与x轴交点的横坐标，也是函数值为零时自变量x的值，也是函数相应的方程的实数根．
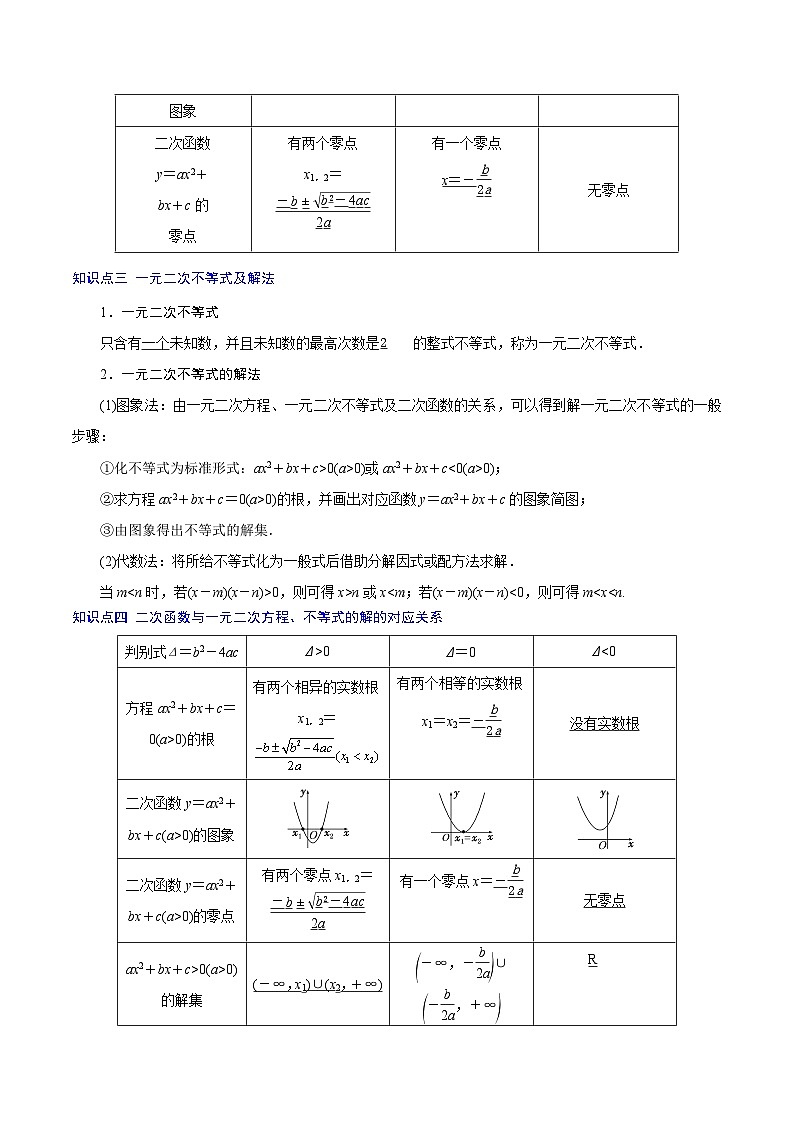
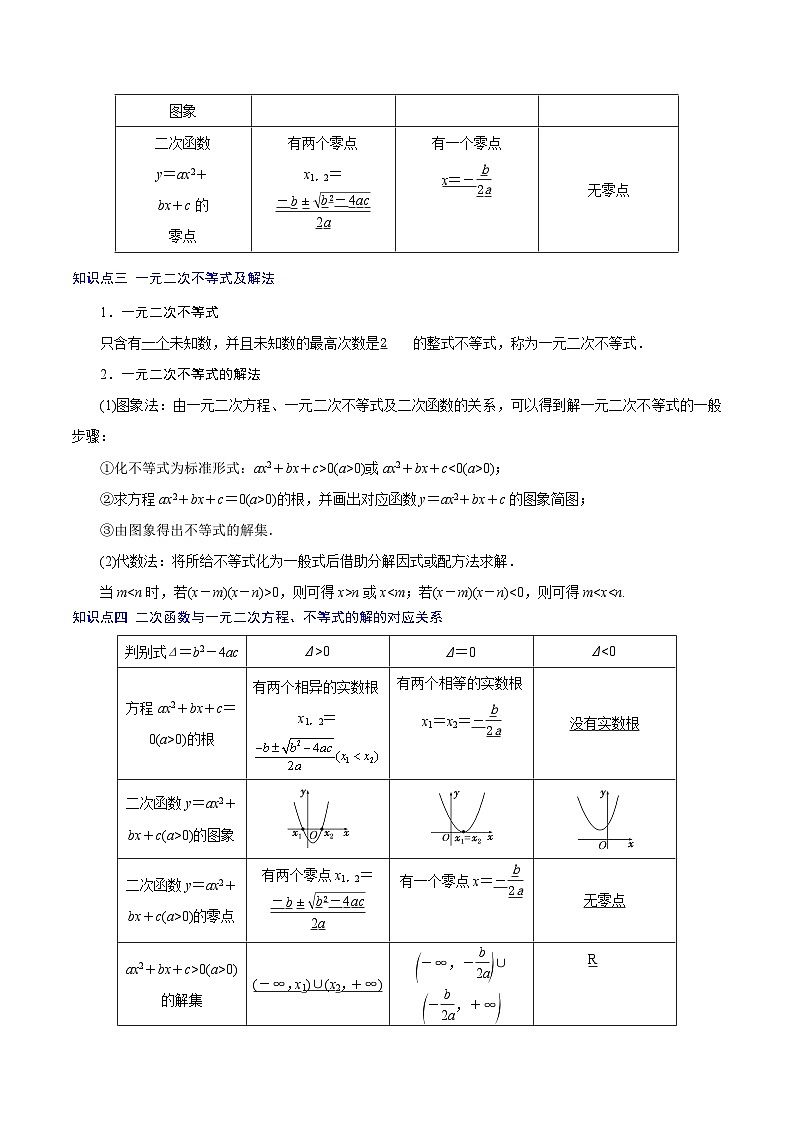
知识点二 一元二次方程的根、二次函数的图象、二次函数的零点之间的关系
当a>0时，一元二次方程ax2＋bx＋c＝0的根、二次函数y＝ax2＋bx＋c的图象、二次函数y＝ax2＋bx＋c的零点之间的关系如表所示：
判别式
Δ＝b2－4ac
Δ>0
Δ＝0
Δ0(a>0)或ax2＋bx＋c0)；
②求方程ax2＋bx＋c＝0(a>0)的根，并画出对应函数y＝ax2＋bx＋c的图象简图；
③由图象得出不等式的解集．
(2)代数法：将所给不等式化为一般式后借助分解因式或配方法求解．
当m0，则可得x>n或x0(a>0)的解集
(－∞，x1)∪(x2，＋∞)
∪

ax2＋bx＋c0)的解集
(x1，x2)


1．函数的角度：一元二次不等式ax2＋bx＋c>0表示二次函数y＝ax2＋bx＋c的函数值大于0，图象在x轴的上方；一元二次不等式ax2＋bx＋c>0的解集即二次函数图象在x轴上方部分的自变量的取值范围．
2．方程的角度：一元二次不等式ax2＋bx＋c>0的解集的端点值是一元二次方程ax2＋bx＋c＝0的根．


考点一：求二次函数的零点
例1 (1)二次函数y＝x2－7x＋12的零点为________；
(2)若函数y1＝x2－ax－b的图象如图所示，则函数y2＝bx2－ax－1的零点是________．

【答案】　(1)3和4　(2)－和－
【解析】(1)由x2－7x＋12＝0得x1＝3，x2＝4.
所以函数y＝x2－7x＋12的零点为3和4.
(2)由题图可知函数y1＝x2－ax－b的零点是2和3，由函数的零点与对应方程根的关系知方程x2－ax－b＝0的两根为2和3，再由根与系数的关系得a＝2＋3＝5，－b＝2×3＝6，即a＝5，b＝－6.所以y2＝－6x2－5x－1，易得y2＝－6x2－5x－1的零点为－和－.
【总结】
二次函数零点的求法
(1)代数法：求出方程ax2＋bx＋c＝0(a≠0)的实数根，即为函数y＝ax2＋bx＋c(a≠0)的零点；
(2)几何法：对于不能用求根公式或分解因式求解的方程，可以将它与对应函数的图象联系起来，利用函数的性质求零点．
变式 求下列函数的零点．
(1)y＝3x2－2x－1；
(2)y＝ax2－x－a－1(a∈R)；
(3)y＝ax2＋bx＋c，其图象如图所示．

【解析】(1)由3x2－2x－1＝0解得x1＝1，x2＝－，所以函数y＝3x2－2x－1的零点为1和－.
(2)①当a＝0时，y＝－x－1，由－x－1＝0得x＝－1，所以函数的零点为－1.
②当a≠0时，由ax2－x－a－1＝0得(ax－a－1)(x＋1)＝0，解得x1＝，x2＝－1，
又－(－1)＝.
当a＝－时，x1＝x2＝－1，函数有唯一的零点－1.
当a≠－且a≠0时，x1≠x2，函数有两个零点－1和.
综上，当a＝0或－时，函数的零点为－1.
当a≠－且a≠0时，函数有两个零点－1和.
(3)由图象可知，函数有两个零点－1和3.


考点二：函数的零点个数的判断与证明
例2 若a>2，求证： 函数y＝(a－2)x2－2(a－2)x－4有两个零点．
【证明】因为Δ＝4(a－2)2＋16(a－2)＝4(a－2)(a＋2)，
又a>2，所以Δ>0，
所以方程(a－2)x2－2(a－2)x－4＝0有两个根，故函数y＝(a－2)x2－2(a－2)x－4有两个零点．
【总结】
二次函数y＝ax2＋bx＋c(a≠0)的零点个数的判断
对于一元二次方程ax2＋bx＋c＝0(a≠0)的根的判别式Δ＝b2－4ac.
(1)Δ>0⇔函数y＝ax2＋bx＋c(a≠0)有两个零点；
(2)Δ＝0⇔函数y＝ax2＋bx＋c(a≠0)有一个零点；
(3)Δ2或a≤－2，
所以函数y＝(a－2)x2－2(a－2)x－4有零点的充要条件为a>2或a≤－2.
（2）求证：函数y＝ax2－x－a(a∈R)有零点．
【证明】当a＝0时，y＝－x，该函数有零点0；
当a≠0时，对于一元二次方程ax2－x－a＝0，Δ＝1＋4a2>0，函数y＝ax2－x－a有两个零点．
综上，函数y＝ax2－x－a(a∈R)有零点．

考点三：二次函数零点的分布探究
例3 (1)判断二次函数y＝－x2－2x＋1在(－3，－2)是否存在零点；
(2)若二次函数y＝(a－2)x2－2(a－2)x－4(a≠2)的两个零点均为正数，求实数a的取值范围．
【解析】(1)由－x2－2x＋1＝0得x1＝－1＋，x2＝－1－，因为－3