





中考数学一轮复习精选专题07 绝对值(讲测练)(2份打包,原卷版+教师版)
展开专题07 绝对值
![]()
1、初步理解绝对值的概念,能求一个数的绝对值,
2、会利用绝对值比较两个负数
的大小。
3、通过应用绝对值解决实际问题体会绝对值的意义和作用。

一、绝对值的概念
1.定义:一个数的绝对值就是数轴上表示![]() 的点与原点的距离,数
的点与原点的距离,数![]() 的绝对值记作
的绝对值记作![]() ,读作
,读作![]() 的绝对值。
的绝对值。
2.绝对值的代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值还是0。
3.绝对值的几何意义:一个数的绝对值就是表示这个数的点到原点的距离,离原点的距离越远,绝对值越大,离原点的距离越近,绝对值越小。
4绝对值的非负性:由于距离总是正数或0,故有理数的绝对值不可能是负数,即对任意有理数![]() ,总有
,总有![]()
![]() 0。
0。
5.互为相反数的两个数的绝对值相等,但绝对值相等的两个数相等或互为相反数。
6.绝对值等于它本身的数一定是非负数,绝对值等于它的相反数的数一定是非正数。
例1、![]() 的绝对值为( )
的绝对值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、绝对值的求法
绝对值是一种运算,这个运算符号是“![]() ”,求一个数的绝对值就是想办法去掉绝对值符号,对于任意有理数
”,求一个数的绝对值就是想办法去掉绝对值符号,对于任意有理数![]() ,有
,有
(1)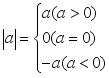 (2)
(2)![]() (3)
(3)![]()
例2、计算|﹣2+1|的结果是( )
A.﹣3 B.3 C.﹣1 D.1

1.(2022·如皋市实验初中九年级期末)-2的绝对值等于( )
A.![]() B.-2 C.
B.-2 C.![]() D.2
D.2
2.(2022·福建省福州杨桥中学)下列各数化简后与![]() 相等的是( )
相等的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.(2022·哈尔滨市虹桥初级中学校九年级二模)下列各数中,绝对值最小的是( )
A.﹣2 B.3 C.0 D.﹣3
4.(2022·福建省福州第一中学九年级开学考试)![]() 的绝对值是( )
的绝对值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.(2022·北京市陈经纶中学分校九年级月考)实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最小的是( )
![]()
A.a B.b C.c D.d
6.(2022·湖北黄石八中九年级三模)﹣ǀ﹣5ǀ的倒数是( )
A.5 B.﹣5 C.![]() D.
D.![]()
7.(2022·重庆实验外国语学校九年级三模)计算:![]() ______.
______.
8.(2022·厦门市松柏中学九年级二模)计算:(-2)2-|-3|=______.
9.(2022·长沙市开福区青竹湖湘一外国语学校)计算:![]()
10.(2022·苏州市胥江实验中学校九年级二模)计算:![]() .
.
专题07 绝对值
一、单选题
1.(2022·河南洛阳)下列各数中,绝对值为![]() 的数是( )
的数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.(2022·河南)下列各数中,最大的数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.(2022·安徽九年级三模)以下各数中绝对值最小的数是( )
A.0 B.-0.5 C.1 D.-2
4.(2022·山东)![]() 的绝对值是 ( )
的绝对值是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.(2022·山东临沂市·九年级一模)![]() 的绝对值是( )
的绝对值是( )
A.![]() B.6 C.
B.6 C.![]() D.
D.![]()
6.(2022·河北)实数a,b在数轴上的位置如图所示,下列结论中正确的是( )
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.(2022·江苏镇江·炎黄外国语学校九年级月考)下列运算错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.(2022·江苏九年级一模)计算![]() 的结果是( )
的结果是( )
A.![]() B.
B.![]() C.2 D.4
C.2 D.4
9.(2022·山东)下列四个数中,其绝对值小于2的数是( )
A.![]() B.
B.![]() C.
C.![]() D.﹣3
D.﹣3
10.(2022·河北邢台·九年级二模)若![]() ,则
,则![]() 的值可以是( )
的值可以是( )
A.![]() B.
B.![]() C.2 D.4
C.2 D.4
二、填空题
11.(2022·河南九年级专题练习)计算:![]() ______.
______.
12.(2022·辽宁盘锦·中考真题)计算:![]() =________
=________
13.(2022·重庆实验外国语学校九年级二模)计算:![]() =______.
=______.
14.(2022·河南省实验中学)请写出一个绝对值大于1小于3的无理数______.
15.(2022·沙坪坝·重庆一中九年级三模)计算:![]() ______.
______.
三、解答题
16.(2022·广西九年级三模)计算:![]() .
.
17.(2022·安徽九年级二模)![]() .
.
18.(2022·全国九年级)在有些情况下,不需要计算出结果也能把绝对值符号去掉,例如:![]() ,
,
根据上面的规律,把(1)(2)(3)中的式子写成去掉绝对值符号的形式,并计算第(4)题.
(1)![]() ___________.
___________.
(2)![]() __________.
__________.
(3)![]() __________.
__________.
(4)![]() .
.
19.(2020·北京101中学)计算:![]() .
.
20.(2022·山东)计算:![]()
21.(2022·山西九年级三模)(1)计算:![]() ;
;
(2)先化简,再求值:![]() ,其中
,其中![]() .
.
22.(2022·合肥市第四十二中学)计算:![]() .
.
23.(2019·浙江)已知有理数![]() ,
,![]() ,
,![]() 在数轴上的位置如图所示,化简:
在数轴上的位置如图所示,化简:![]() .
.
![]()
中考数学一轮复习精选专题24 求几何图形的面积(讲测练)(2份打包,原卷版+教师版): 这是一份中考数学一轮复习精选专题24 求几何图形的面积(讲测练)(2份打包,原卷版+教师版),文件包含中考数学一轮复习精选专题24求几何图形的面积讲测练教师版doc、中考数学一轮复习精选专题24求几何图形的面积讲测练原卷版doc等2份试卷配套教学资源,其中试卷共39页, 欢迎下载使用。
中考数学一轮复习精选专题22 四边形(讲测练)(2份打包,原卷版+教师版): 这是一份中考数学一轮复习精选专题22 四边形(讲测练)(2份打包,原卷版+教师版),文件包含中考数学一轮复习精选专题22四边形讲测练教师版doc、中考数学一轮复习精选专题22四边形讲测练原卷版doc等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。
中考数学一轮复习精选专题20 多边形内角和定理的应用(讲测练)(2份打包,原卷版+教师版): 这是一份中考数学一轮复习精选专题20 多边形内角和定理的应用(讲测练)(2份打包,原卷版+教师版),文件包含中考数学一轮复习精选专题20多边形内角和定理的应用讲测练教师版doc、中考数学一轮复习精选专题20多边形内角和定理的应用讲测练原卷版doc等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。












