中考数学一轮复习精选专题04 实数与二次根式的运算（讲测练）（2份打包，原卷版+教师版）

专题04 实数与二次根式的运算

1.了解有理数、无理数、实数的概念；

2.了解乘方与开方、平方根、算术平方根、立方根的概念，并理解这两种运算之间的关系；

3.掌握实数的运算法则，并能灵活运用；

4.了解二次根式的概念；

5.掌握二次根式的运算法则，并能灵活运用。

一、实数的基本概念 

1．无理数的概念：

（1）定义：无限不循环小数叫做无理数.

（2）解读：

   1）无理数的两个重要特征：①无限小数；②不循环.

   2）无理数的常见类型：

     ①具有特定意义的数。如π等；

     ②……（每相邻两个1之间依次多一个2）等；

     ③开方开不尽的数，如，等.  那么，是否所有带根号的数都是无理数呢

   3）有理数与无理数的区别：有理数总可以表示为有限小数或无限循环小数，反之，有限小数和无限循环小数也必定是有理数；而无理数是无限不循环小数，无限不循环小数也必定是无理数.

例1、下列实数、sin60°、、、3.14159、-、、中无理数有（  ）个

A．1      B．2        C．3       D．4

2．实数的概念及分类：

（1）定义：有理数和无理数统称为实数.

（2）分类：

①按定义分：

②按性质分：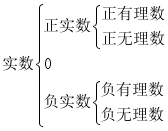

（3）实数的性质：

     ①相反数：与互为相反数.

     ②绝对值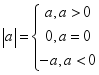：或或

（4）实数和数轴上的点是一一对应的.

π是一个超越数，用尺规作图的方法是不能在数轴上表示的；可以用物理方法来表示：用一个直径为1的圆形从数轴的零点开始转动，正好转一圈的那个点就是π，因为直径为1的圆的周长为π。

（5）实数的运算顺序：先算乘方、开方、再算乘除、最后算加减，同级运算按照从左到右的顺序进行，有括号的先算括号里的。

（6）实数中非负数的四种形式及其性质：

形式：①；②；③（）；④中.

性质：①非负数有最小值0；②有限个非负数之和仍然是非负数；③几个非负数之和等于0，则每个非负数都等于0.

（7）实数中无理数的常见类型：

①所有开不尽的方根都是无理数，且不可认为带根号的数都是无理数；

②圆周率π及含有π的数是无理数，例如：等；

③…….

例2、在中，哪些是有理数? 哪些是无理数?

例3、计算：+|2﹣3|﹣（）﹣1﹣（2015+）0．

例4、|﹣1|+20120﹣（﹣）﹣1﹣3tan30°．

【变式】计算：

二、二次根式的概念

1. 二次根式的定义：形如（a≥0）的式子叫做二次根式

2. 二次根式应满足两个条件：

第一，有二次根号“”。

第二，被开方数是正数或0。

第三，二次根式（≥0）表示非负数的算术平方根。

例5、当x取何值时，的值最小？最小值是多少？

3. 性质

(1)=a（a≥0）．

(2)      （a≥0）    （a＜0）

(3)=·（a≥0，b≥0）     ·＝（a≥0，b≥0）

(4)=（a≥0，b>0）            =（a≥0，b>0）

例6、计算：； 

4. 最简二次根式

二次根式（）中的称为被开方数．满足下面条件的二次根式我们称为最简

二次根式：

(1)被开方数的因数是整数，因式是整式（被开方数不能存在小数、分数形式）；

(2)被开方数中不含能开得尽方的因数或因式；

(3)分母中不含二次根式。

二次根式的计算结果要写成最简根式的形式．

5. 同类二次根式

几个二次根式化成最简二次根式后，如果被开方数相同，这几个二次根式叫同类二次根式。

合并同类二次根式：．同类二次根式才可加减合并．

1．（2022·山东济宁学院附属中学九年级期末）实数﹣，|﹣|，0，中，最小的数是（　　）

A．﹣ B．|﹣| C．0 D．

2．（2022·福建三明一中九年级开学考试）下列实数中，无理数是（　　）

A．3.14 B． C． D．

3．（2022·四川绵阳·中考真题）计算的结果是（    ）

A．6 B． C． D．

4．（2022·重庆实验外国语学校九年级月考）估计的值应在（    ）

A．1和2之间 B．2和3之间 C．3和4之间 D．4和5之间

5．（2022·常熟市第一中学九年级开学考试）在下列四个实数中，最小的数是（    ）

A． B． C．0 D．－

6．（2022·江苏泰州中学附属初中九年级三模）下列运算正确的是（    ）

A． B．

C．（a－b）（－a＋b）=－a2－2ab－b2 D．

7．（2022·北京交通大学附属中学）计算：

（1）

（2）

8．（2022·陕西西安市·交大附中分校九年级模拟预测）计算：．

9．（2022·长沙市雅礼实验中学九年级月考）计算：．

10．（2022·西宁市教育科学研究院中考真题）计算：．

专题04 实数与二次根式的运算

一、单选题

1．（2022·广东广州·铁一中学九年级二模）下列计算正确的是（    ）

A． B． C． D．

2．（2022·广东实验中学九年级三模）的相反数是（    ）

A． B． C． D．

3．（2022·山东日照·中考真题）在下列四个实数中，最大的实数是（　　）

A．-2 B． C． D．0

4．（2022·长沙市雅礼实验中学九年级月考）下列实数中，最大的数是（    ）

A．π B． C．﹣2 D．3

5．（2022·长沙市南雅中学九年级期中）下列计算错误的是（　　）

A．(π﹣3.14)0＝0 B．

C．(x2)3＝x6 D．a6÷a2＝a4

6．（2022·长沙市雅礼实验中学九年级月考）下列各运算中，正确的运算是（    ）

A． B．（2a）3＝8a3

C．a8÷a4＝a2 D．（a﹣b）2＝a2﹣b2

7．（2022·河南九年级期中）计算：＝（　　）

A．﹣ B．0 C． D．

8．（2022·河南九年级期中）下列运算正确的是（　　）

A． B．＝2

C．＝2﹣ D．＝3a2

9．（2022·广西南宁十四中）下列属于最简二次根式的是（    ）

A． B． C． D．

10．（2022·沙坪坝·重庆八中九年级月考）估计的值应在（  ）

A．1和2之间 B．2和3之间

C．3和4之间 D．4和5之间

二、填空题

11．（2022·莆田第二十五中学九年级月考）估计的值应在_____．

12．（2022·沭阳县怀文中学九年级月考）若式子在实数范围内有意义，则应满足的条件是_______________．

13．（2022·沙坪坝·重庆八中九年级月考）计算：__________．

14．（2022·重庆市育才中学九年级开学考试）计算________．

15．（2022·西安市铁一中学九年级模拟预测）计算：____________．

三、解答题

16．（2022·山东九年级期中）已知x、y是实数，若，求xy的立方根．

17．（2022·湖南师大附中博才实验中学九年级二模）计算：

18．（2022·四川广安中学）计算：

（1）；

（2）．

19．（2022·西城·北京四中）计算：．

20．（2022·深圳市罗湖区翠园初级中学）先化简，再求值：，其中m＝．

21．（2022·福建九年级模拟预测）计算：

22．（2022·福建三明一中九年级开学考试）计算

（1）

（2）

23．（2022·如皋市实验初中九年级期末）（1）计算；

（2）先化简，再求代数式的值，其中．