考点跟踪突破10　函数及其图象课件PPT

这是一份考点跟踪突破10　函数及其图象课件PPT，共22页。PPT课件主要包含了x≥－1且x≠0等内容，欢迎下载使用。

2．(2014·衡阳)小明从家出发，外出散步，到一个公共阅报栏前看了一会儿报后，继续散步了一段时间，然后回家．如图描述了小明在散步过程中离家的距离s(米)与散步所用的时间t(分)之间的函数关系．根据图象，下列信息错误的是( )A．小明看报用时8分钟B．公共阅报栏距小明家200米C．小明离家最远的距离为400米D．小明从出发到回家共用时16分钟
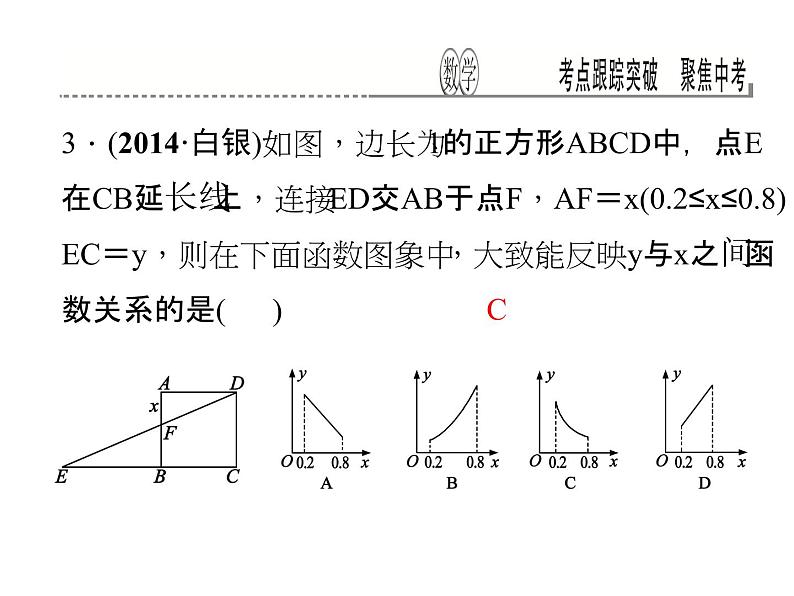
3．(2014·白银)如图，边长为1的正方形ABCD中，点E在CB延长线上，连接ED交AB于点F，AF＝x(0.2≤x≤0.8)，EC＝y，则在下面函数图象中，大致能反映y与x之间函数关系的是( )
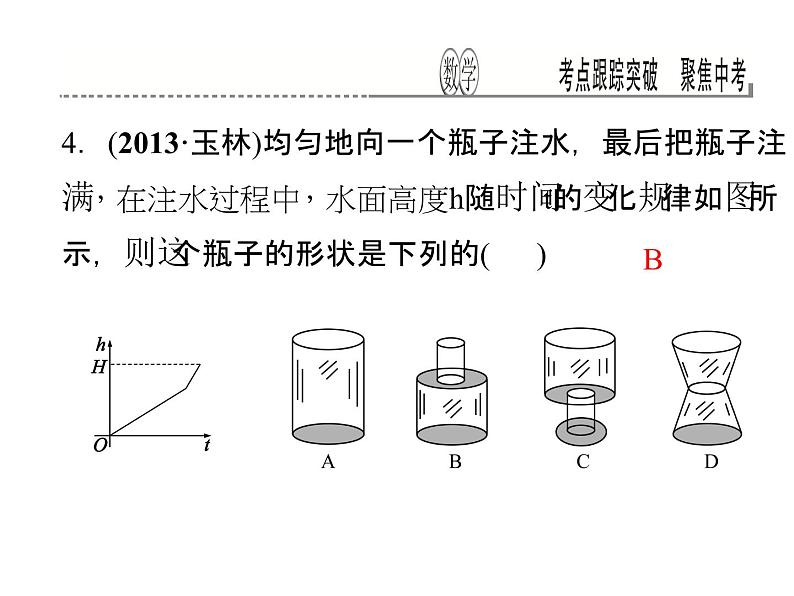
4．(2013·玉林)均匀地向一个瓶子注水，最后把瓶子注满，在注水过程中，水面高度h随时间t的变化规律如图所示，则这个瓶子的形状是下列的( )
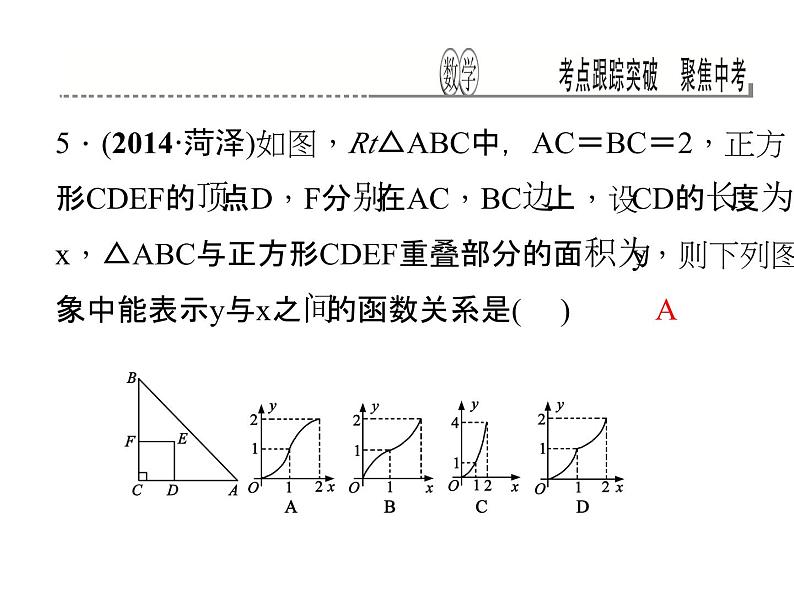
5．(2014·菏泽)如图，Rt△ABC中，AC＝BC＝2，正方形CDEF的顶点D，F分别在AC，BC边上，设CD的长度为x，△ABC与正方形CDEF重叠部分的面积为y，则下列图象中能表示y与x之间的函数关系是( )
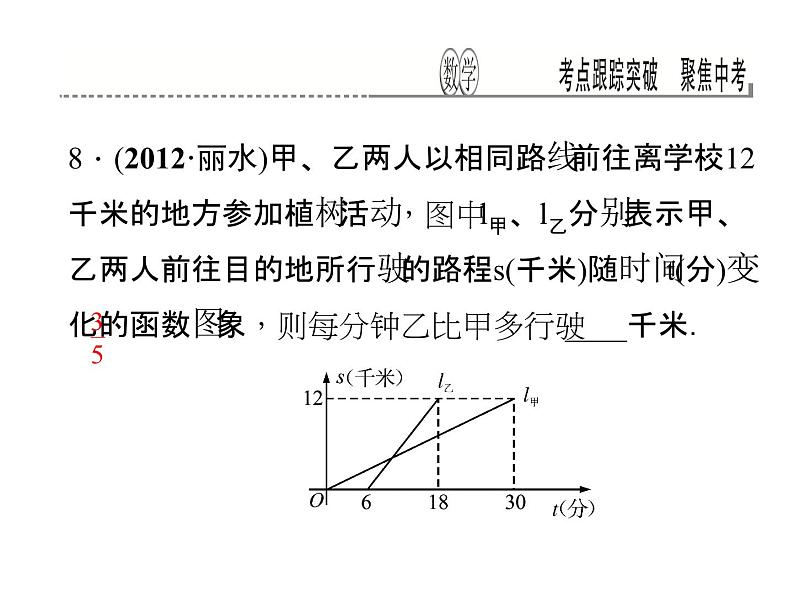
8．(2012·丽水)甲、乙两人以相同路线前往离学校12千米的地方参加植树活动，图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程s(千米)随时间t(分)变化的函数图象，则每分钟乙比甲多行驶____千米．
9．将完全相同的平行四边形和完全相同的菱形镶嵌成如图所示的图案．设菱形中较小角为x度，平行四边形中较大角为y度，则y与x的关系式是 ．
10．(2014·金华)小明从家跑步到学校，接着马上原路步行回家．如图是小明离家的路程y(米)与时间t(分)的函数图象，则小明回家的速度是每分钟步行____米．
三、解答题(共40分)11．(10分)某班师生组织植树活动，上午8时从学校出发，到植树地点植树后原路返校，如图为师生离校路程s与时间t之间的图象．请回答下列问题：
(1)求师生何时回到学校？
(2)如果运送树苗的三轮车比师生迟半小时出发，与师生同路匀速前进时，早半小时到达植树地点，请在图中，画出该三轮车运送树苗时，离校路程s与时间t之间的图象，并结合图象直接写出三轮车追上师生时，离学校的路程；
(3)如果师生骑自行车上午8时出发，到植树地点后，植树需2小时，要求14时前返回到学校，往返平均速度分别为每时10 km，8 km.现有A，B，C，D四个植树点与学校的路程分别是13 km，15 km，17 km，19 km，试通过计算说明哪几个植树点符合要求．
12．(10分)(2013·绍兴)某市出租车计费方法如图所示，x(km)表示行驶里程，y(元)表示车费，请根据图象回答下列问题：(1)出租车的起步价是多少元？当x＞3时，求y关于x的函数解析式；(2)若某乘客有一次乘出租车的车费为32元，求这位乘客乘车的里程．
13．(10分)(2012·株洲)如图，在△ABC中，∠C＝90°，BC＝5米，AC＝12米，M点在线段CA上，从C向A运动，速度为1米/秒；同时N点在线段AB上，从A向B运动，速度为2米/秒，运动时间为t秒．(1)当t为何值时，∠AMN＝∠ANM?(2)当t为何值时，△AMN的面积最大？并求出这个最大值．
实际应用(3)已知某汽车的一次运输成本包含以下三个部分：一是固定费用，共360元；二是燃油费，每千米为1.6元；三是折旧费，它与路程的平方成正比，比例系数为0.001.设该汽车一次运输的路程为x千米，求当x为多少时，该汽车平均每千米的运输成本最低？最低是多少元？