

2023年甘肃省陇南市西和县中考数学二模试卷(含解析)
展开2023年甘肃省陇南市西和县中考数学二模试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 的倒数是( )
A. B. C. D.
2. 的发现使人类了解到一个全新的碳世界如图是的分子结构图,包括个正六边形和个正五边形,其中正五边形的一个内角的大小是( )
A.
B.
C.
D.
3. 乌鞘岭是陇中高原和河西走廊的天然分界,主峰海拔超过米若用米表示乌鞘岭主峰的海拔高度,则满足的关系为( )
A. B. C. D.
4. 关于的一元二次方程有实数根,则的取值范围是( )
A. B. C. D.
5. 如图,和是以点为位似中心的位似图形若,则下列结论正确的是( )
A.
B.
C.
D.
6. 月日是世界无烟日,小林为了了解所住小区成年人吸烟的人数,随机调查了个成年人,结果有个成年人吸烟关于此次调查,下列说法错误的是( )
A. 调查的方式是抽样调查 B. 样本容量是
C. 小林还需要知道小区里成年人的人数 D. 小林所住小区共有个成年人吸烟
7. 利用圆的等分,在半径为的圆中作出如图的图案,则相邻两等分点之间的距离为( )
A.
B.
C.
D.
8. 古代劳动人民在实际生活中有这样一个问题:“耠子耧六十三,百根腿地里钻,两者各几何?”其大意为:耠子和耧共有个,共有条腿,问有多少个耠子,多少个耧?耠子有一条腿,耧有两条腿设耠子有个,耧有个,则下列方程组正确的是( )
A. B. C. D.
9. 如图是一个几何体的三视图,主视图和左视图均是面积为的等腰三角形,俯视图是直径为的圆,则这个几何体的全面积是( )
A.
B.
C.
D.
10. 如图,动点从正六边形的点出发,沿以的速度匀速运动到点,图是点运动时,的面积随着时间的变化的关系图象,则正六边形的边长为( )
A. B. C. D.
二、填空题(本大题共8小题,共32.0分)
11. 化简:______.
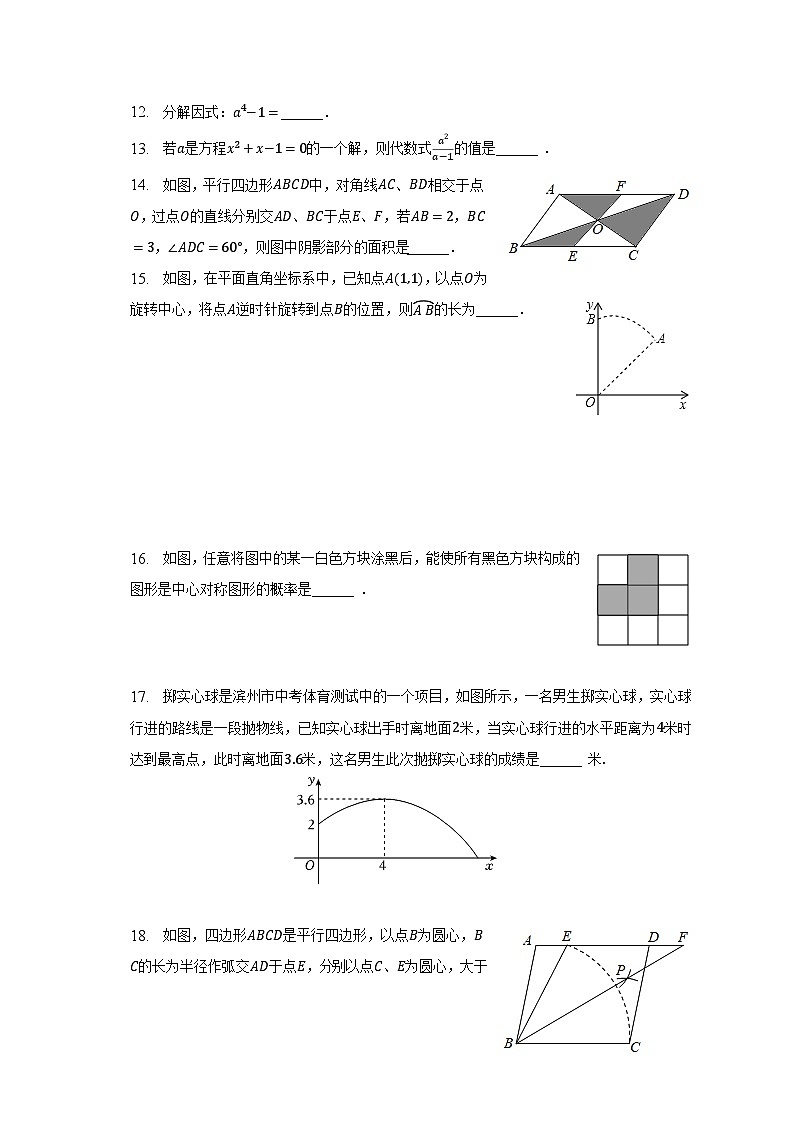
12. 分解因式:______.
13. 若是方程的一个解,则代数式的值是______ .
14. 如图,平行四边形中,对角线、相交于点,过点的直线分别交、于点、,若,,,则图中阴影部分的面积是______.
15. 如图,在平面直角坐标系中,已知点,以点为旋转中心,将点逆时针旋转到点的位置,则的长为______.
16. 如图,任意将图中的某一白色方块涂黑后,能使所有黑色方块构成的图形是中心对称图形的概率是______ .
17. 掷实心球是滨州市中考体育测试中的一个项目,如图所示,一名男生掷实心球,实心球行进的路线是一段抛物线,已知实心球出手时离地面米,当实心球行进的水平距离为米时达到最高点,此时离地面米,这名男生此次抛掷实心球的成绩是______ 米
18. 如图,四边形是平行四边形,以点为圆心,的长为半径作弧交于点,分别以点、为圆心,大于的长为半径作弧,两弧交于点,作射线交的延长线于点,,,则的长为______.
三、计算题(本大题共1小题,共6.0分)
19. 计算:.
四、解答题(本大题共9小题,共82.0分。解答应写出文字说明,证明过程或演算步骤)
20. 本小题分
化简:.
21. 本小题分
今年是“一带一路”倡议提出及建设开启的十周年十年来,我国与个国家、个国际组织签署了余份共建“一带一路”合作文件,在基础设施建设、能源建设、交通运输、脱贫等多个方面取得成果,为多个国家的合作发展带来好消息如图,北京与雅典、莫斯科建立了“一带一路”贸易合作关系,记北京为地,莫斯科为地,雅典为地,若想建一个货物中转仓,使其到,,三地的距离相等,那么如何选择中转仓的位置?请你用尺规作图设计出中转仓的位置,保留作图痕迹,不用说明理由,并描黑作图痕迹.
22. 本小题分
人工智能越来越多地应用于现实生活,某科技小组的成员小星在一次就餐中,对餐厅使用的“送菜机器人”很感兴趣,于是他与小组成员一起研制了一个简易的智能机器人如图,机器人底座固定在桌面桌面足够大上,且,,,和可以分别绕点,自由转动,且,,始终在同一平面内机器人工作时,某时刻的示意图如图所示,,,求此时点到桌面的距离结果保留一位小数.
参考数据:,,,,.
23. 本小题分
某校在践行以“安全在我心中,你我一起行动”为主题的手抄报评比活动中,共设置了“交通安全、消防安全、饮食安全、校园安全”四个主题内容,推荐甲和乙两名学生参加评比,若他们每人从以上四个主题内容中随机选择一个,每个主题被选择的可能性相同.
甲选择“校园安全”主题的概率为______ ;
请用画树状图法或列表法求甲和乙选择不同主题的概率.
24. 本小题分
“垃圾分类新时尚,文明之风我先行”某地自开展“创卫、创文工作”以来,广大群众积极参与各项工作新修订的生活垃圾分类标准为厨余垃圾、有害垃圾、其他垃圾和可回收物四类,为了促使居民更好地了解垃圾分类知识,小珂所在的小区随机抽取了名居民进行线上垃圾分类知识测试将参加测试的居民的成绩进行收集、整理,绘制成如下频数分布表和频数分布直方图:
线上垃圾分类知识测试频数分布表
成绩分组 | 频数 |
C.成绩在这一组的成绩为,,,,,,,,,,,.
根据以上信息,回答下列问题:
表中的值为______ ;
请补全频数分布图;
小到居住的社区大约有居民人,若测试成绩达到分为良好,那么估计小珂所在的社区成绩良好的人数约为______ 人;
若测试成绩在前十五名的居民可以领到“垃圾分类知识小达人”奖章已知居民的得分为分,请说明居民是否可以领到“垃圾分类知识小达人”奖章?
25. 本小题分
如图,在平面直角坐标系中,为坐标原点,的边垂直于轴,垂足为点,反比例函数的图象经过的中点,交于点,且若点的坐标为.
求反比例函数的表达式.
设点是轴上一动点,若的面积等于,求点的坐标.
26. 本小题分
如图,是的直径,是上一点,于点,过点作的切线,交的延长线于点,连接并延长与的延长线交于点.
求证:是的切线;
若,,求的长.
27. 本小题分
某校数学活动小组探究了如下数学问题:
问题发现:如图,中,,点是底边上一点,连接,以为腰作等腰,且,连接、则和的数量关系是______ ;
变式探究:如图,中,,点是腰上一点,连接,以为底边作等腰,连接,判断和的数量关系,并说明理由;
问题解决;如图,正方形的边长为,点是边上一点,以为对角线作正方形,连接若设正方形的面积为,求与的函数关系式.
28. 本小题分
如图,抛物线与坐标轴相交于,两点,点为直线下方抛物线上一动点,过点作轴的垂线,垂足为;交直线于点.
求抛物线的函数表达式;
求的最大值;
过点的直线交轴于点,交直线于点,是轴上一点,当四边形是矩形时,求点的坐标.
答案和解析
1.【答案】
【解析】解:的倒数是.
故选:.
乘积是的两数互为倒数,由此即可得到答案.
本题考查倒数,关键是掌握倒数的定义.
2.【答案】
【解析】解:正五边形的内角和为:,
该正五边形的每个内角为:,
故选:.
根据多边形的内角和公式及正多边形性质计算即可.
本题考查多边形的内角和与正多边形的性质,此为基础且重要知识点,必须熟练掌握.
3.【答案】
【解析】解:乌鞘岭是陇中高原和河西走廊的天然分界,主峰海拔超过米,米表示乌鞘岭主峰的海拔高度,
,
故选:.
根据乌鞘岭是陇中高原和河西走廊的天然分界和主峰海拔超过米得出答案即可.
本题考查了不等式的意义,能正确列出不等式是解此题的关键.
4.【答案】
【解析】解:根据题意得:,
解得.
故选:.
先根据判别式的意义得到,然后解关于的一元一次不等式即可.
本题考查了根的判别式:一元二次方程的根与有如下关系:当时,方程有两个不相等的实数根;当时,方程有两个相等的实数根;当时,方程无实数根.
5.【答案】
【解析】解:和是以点为位似中心的位似图形,,
,故A错误,不符合题意;
,故B正确,符合题意;
,故C错误,不符合题意;
,故D错误,不符合题意.
故选:.
根据位似三角形的性质逐项分析即可得出答案.
本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.
6.【答案】
【解析】解:、调查的方式是抽样调查,原说法正确,故此选项不符合题意;
B、样本容量是,原说法正确,故此选项不符合题意;
C、小林还需要知道小区里成年人的人数,原说法正确,故此选项不符合题意;
D、小林所住小区占的成年人吸烟,原说法错误,故此选项符合题意.
故选:.
直接利用样本容量的定义以及抽样调查的定义分别分析得出答案.
此题主要考查了样本容量以及抽样调查的定义,正确把握相关定义是解题关键.
7.【答案】
【解析】解:如图,连接,,
,,
是等边三角形,
,
相邻两等分点之间的距离为,
故选:.
如图,连接,,根据等边三角形的判定和性质定理即可得到结论.
本题考查了正多边形与圆,等边三角形的判定和性质,熟练掌握正六边形的性质是解题的关键.
8.【答案】
【解析】解:耠子和耧共有个,
;
耠子和耧共有条腿,
.
根据题意可列出方程组.
故选:.
根据“耠子和耧共有个,共有条腿”,即可得出关于,的二元一次方程组,此题得解.
本题考查了由实际问题抽象出二元一次方程组,找准等量关系,正确列出二元一次方程组是解题的关键.
9.【答案】
【解析】解:圆锥的高,
母线长,
圆锥的全面积.
故选:.
依据题意可得这个几何体为圆锥,其全面积侧面积底面积.
本题考查由三视图判断几何体,圆锥的计算.用到的知识点为:有个视图为三角形,另一个视图为圆的几何体是圆锥.
10.【答案】
【解析】解:如图,连接,,,交于点
由正六边形的对称性可得,易证
为等边三角形,为边上的高线
动点从正六边形的点出发,沿以的速度匀速运动
当点运动到点时的面积取最大值
设,则,
或舍
正六边形的每个内角均为
在中,
正六边形的边长为
故选:.
如图,连接,,,交于点,证明为等边三角形,根据的最大值求得的边长,再在直角三角形中用三角函数求得的长即可.
本题考查了动点问题的函数图象,以图中值的最大值为突破口,求得等边三角形的边长,是解题的关键.
11.【答案】
【解析】解:.
故答案为:.
利用二次根式的性质即可化简.
本题考查二次根式的化简,解题的关键是学会二次根式的化简方法,属于中考常考题型.
12.【答案】
【解析】解:,
,
.
故答案为:.
运用平方差公式进行两次分解即可.
本题考查了用平方差公式分解因式,注意利用平方差公式进行两次分解,注意分解要彻底.
13.【答案】
【解析】解:是方程的一个解,
,
,
,
故答案为:.
将代入一元二次方程可以得到,然后代入代数式中计算即可.
本题考查一元二次方程的解,明确方程的解一定使得方程成立是解题的关键.
14.【答案】
【解析】解:平行四边形中,对角线、相交于点,
,
阴影部分面积等于的面积,即为▱面积的一半,
过点作于点,
,,
,,
,
阴影部分面积为,
故答案为:.
由平行四边形的性质可知阴影部分面积为平行四边形面积的一半,进而可求出结果.
本题考查平行四边形的性质,熟练掌握平行四边形对边平行且相等的性质是解题关键.
15.【答案】
【解析】解:点,
,且点在第一象限的角平分线上,
以点为旋转中心,将点逆时针旋转到点的位置,
,
的长为.
故答案为.
由点,可得,且点在第一象限的角平分线上,则,再根据弧长公式计算即可.
本题考查弧长的计算,以及旋转中的坐标变化.
16.【答案】
【解析】解:如图,当涂黑、、区域时,所有黑色方块构成的图形是中心对称图形,
,
故答案为:.
把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形称为中心对称图形,结合概率公式计算即可.
本题考查了中心对称图形的定义,概率的计算,正确理解中心对称图形的定义,掌握概率公式是解题的关键.
17.【答案】
【解析】解:抛物线的顶点,设抛物线的解析式为:
把代入解析式可求得,
抛物线的解析式为:
当时,
解得:舍去,,
即这名男生此次抛掷实心球的成绩是米;
故答案是:.
已知抛物线的顶点,抛物线与轴的交点,可设抛物线的顶点式,并求出解析式;要得到实心球的成绩,即求出与轴交点对应的的值即可.
本题考查点的坐标的求法及二次函数的实际应用,此题为数学建模题,借助二次函数解决实际问题.
18.【答案】
【解析】解:由尺规作图知,平分,
,
四边形是平行四边形,
,
,
,
,
过点作于,则,
,
,
,
,
故答案为:.
由尺规作图知,平分,再利用平行线的性质和角平分线的定义可知,过点作于,则,再根据含角的直角三角形的性质可得,从而得出的长.
本题主要考查了平行四边形的性质,尺规作图,等腰三角形的性质等知识,证明是解题的关键.
19.【答案】解:原式
.
【解析】利用负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值分别化简得出答案.
此题主要考查了负整数指数幂的性质以及零指数幂的性质和特殊角的三角函数值等知识,正确化简各数是解题关键.
20.【答案】解:原式
.
【解析】先通分算括号内的,把除化为乘,再约分即可.
本题考查分式的混合运算,解题的关键是掌握分式的基本性质,把分式通分和约分.
21.【答案】解:如图,点即为所求.
【解析】作线段,的垂直平分线交于点,点即为所求.
本题考查作图应用与设计作图,线段的垂直平分线的性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题.
22.【答案】解:过点作,垂足为,过点作,交的延长线于点,延长与相交于点,
由题意得:,,
,
,
,
,
,
,
在中,,
,
,
,
,
在中,,
,
,
此时点到桌面的距离约为.
【解析】过点作,垂足为,过点作,交的延长线于点,延长与相交于点,根据题意可得:,,根据垂直定义可得,再利用平角定义可得,从而利用直角三角形的两个锐角互余可得,然后利用平角定义可得,在中,利用锐角三角函数的定义求出的长,从而求出的长,最后在中,利用锐角三角函数的定义求出的长,从而利用线段的和差关系进行计算,即可解答.
本题考查了解直角三角形的应用,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
23.【答案】
【解析】解:由题意,甲选择“校园安全”主题的概率为,
故答案为:;
设交通安全、消防安全、饮食安全、校园安全分别为、、、,
画树状图为:
共有种等可能的结果,其中甲和乙选择不同主题的结果有种,
则甲和乙选择不同主题的概率为.
直接利用概率公式求解即可;
画树状图,求得所有等可能的结果数,再找出甲和乙选择不同主题的结果数,利用概率公式求解即可.
本题考查的是用列表法或画树状图法求概率.画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
24.【答案】
【解析】解:由题意可得,表中的值为:,
故答案为:;
由值的值为,
由频数分布表可知这一组的频数为,
补全的频数分布直方图如图所示:
估计小珂所在的社区良好的人数约为人,
故答案为:;
由题意可得,分是第名,
故居民可以领到“垃圾分类知识小达人”奖章.
根据题意,可以得到样本容量,然后即可计算出的值;
根据频数分布表中的数据和的值,可以将频数分布表补充完整;
根据题目中的数据,可以计算出小珂所在的社区良好的人数;
根据题目中的数据,可以得到分是第多少名,从而可以得到居民是否可以领到“垃圾分类知识小达人”奖章.
本题考查频数分布表、频数分布直方图、用样本估计总体、样本容量,解答本题的关键是明确频率频数总数.
25.【答案】解:点的坐标为,,
点的坐标为,
点是的中点,
点的坐标为,
把点、的坐标代入,
得,
解得:,
则反比例函数的解析式为:;
设点的坐标为,
由知,,
,
,
当点在点左侧时,;
当点在点右侧时,.
综上所述,点的坐标为或.
【解析】根据线段中点的概念求出点的坐标,解方程组求出,得出反比例函数的解析式;
设点的坐标为,根据的面积等于求出的值即可.
本题考查的是待定系数法求反比例函数解析式,熟知待定系数法求反比例函数解析式的一般步骤是解题的关键.
26.【答案】证明:如图,连接,
,经过原点,
垂直平分,
,
在和中,
,
≌,
,
是的切线,
,
,即,
是的切线.
连接,如图,
是的直径,
,
,
,
,
,
,
∽,
::,
,
,,
,,
,
.
【解析】如图,连接,由“垂径定理”可知,垂直平分,所以,由可证明≌,所以,由切线的性质可知,,所以,即,由此可得结论;
连接,根据正切函数可得的长,利用勾股定理可得的长,因为是的直径,所以,所以,因为,所以,易证∽,所以::,代入数值可得答案.
本题考查了切线的性质及判定,相似三角形的判定和性质,全等三角形的判定和性质,证明圆的切线的问题常用的思路是根据切线的判定定理转化成证明垂直的问题.
27.【答案】
【解析】解:是等腰直角三角形,
,
在中,,,
,,
.
在和中,
,
≌,
,
故答案为:;
,理由如下:
是等腰直角三角形,中,,,
,.
,
,
∽,
,
;
连接,
四边形是正方形,四边形是正方形,
和都是等腰直角三角形,
,,
,
,
∽,
,
,,
,,
在中,,
即,
是正方形的对角线,正方形的面积为,
,
,
,,
.
根据已知条件利用边角边证明≌,再利用全等三角形的性质即可得到和的数量关系;
根据任意等腰直角三角形的直角边与斜边的比是相等的,利用两边成比例且夹角相等的判定定理证明∽,之后再由相似三角形对应边成比例即可得到和的数量关系;
连接,先由正方形的性质判断出和都是等腰直角三角形,再利用与第二问同样的方法证出∽,由相似比求出,再由勾股定理求得,则可列出关系式.
本题考查四边形的综合应用,掌握正方形的性质,等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,正确识图并能熟练地掌握几何图形的性质与判定定理进行证明是解题的关键.
28.【答案】解:抛物线与坐标轴相交于,两点,
,
解得,
抛物线的函数表达式为;
设直线的解析式为,把,代入得,
,
解得,
直线的解析式为,
设点的坐标是,则点的坐标是,
,
当时,的最大值是;
过点的直线交轴于点,
当时,,
点的坐标为,
,
,
四边形是矩形,
,,
,
过点作轴的垂线,垂足为,
轴,
,,
≌,
,
,,
,
≌
,
,
,
点的坐标是.
【解析】利用待定系数法即可求解抛物线的函数表达式;
利用待定系数法求出直线的解析式为,设点的坐标是,则点的坐标是,得到,根据二次函数的性质即可得到的最大值;
先求出,得到,根据四边形是矩形,得到,,则,由轴得到,,则≌,,同理可得≌,,则,得到,得到点的坐标.
此题考查了二次函数图象和性质、矩形的性质、全等三角形的判定和性质,数形结合和准确计算是解题的关键.
2023年甘肃省陇南市西和县中考数学二模试卷(含解析): 这是一份2023年甘肃省陇南市西和县中考数学二模试卷(含解析),共26页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2023年甘肃省陇南市西和县中考冲刺数学模拟试卷(五): 这是一份2023年甘肃省陇南市西和县中考冲刺数学模拟试卷(五),共8页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023年甘肃省陇南市西和县中考数学一模试卷(含答案): 这是一份2023年甘肃省陇南市西和县中考数学一模试卷(含答案),共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












