【暑假提升】(人教A版2019)数学高一（升高二）暑假-1.4.1《第2课时 空间中直线、平面的平行、垂直》讲学案（必修1）

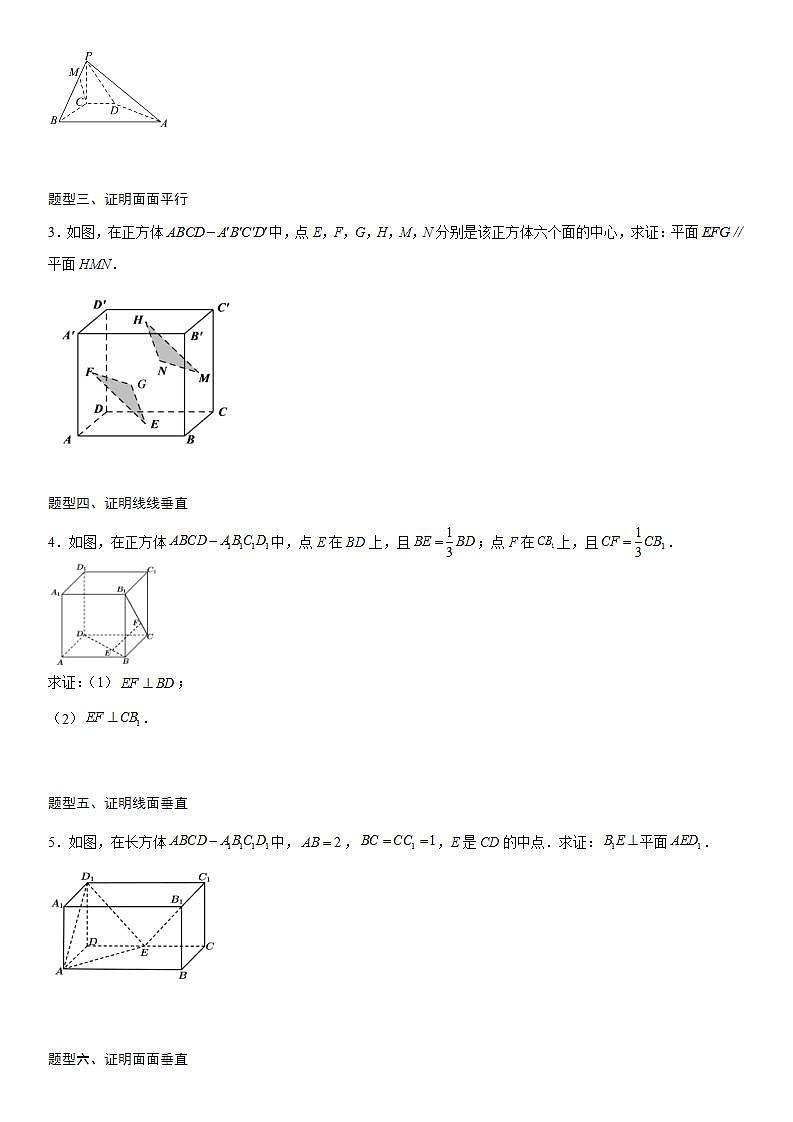
空间中直线、平面的平行、垂直知识点一　线线平行的向量表示设u1，u2分别是直线l1，l2的方向向量，则l1∥l2⇔u1∥u2⇔∃λ∈R，使得u1＝λu2.知识点二　线面平行的向量表示设u是直线 l 的方向向量，n是平面α的法向量，l⊄α，则l∥α⇔u⊥n⇔u·n＝0.知识点三　面面平行的向量表示设n1 ，n2 分别是平面α，β的法向量，则α∥β⇔n1∥n2⇔∃λ∈R，使得n1＝λn2 .知识点四　线线垂直的向量表示设 u1，u2 分别是直线 l1 , l2 的方向向量，则l1⊥l2⇔u1⊥u2⇔u1·u2＝0.知识点五　线面垂直的向量表示设u是直线 l 的方向向量，n是平面α的法向量， l⊄α，则l⊥α⇔u∥n⇔∃λ∈R，使得u＝λn.知识点六　面面垂直的向量表示设n1，n2 分别是平面α，β的法向量，则α⊥β⇔n1⊥n2⇔n1·n2＝0.题型一、证明线线平行1．如图，在正方体中，棱长为2，M，N分别为，AC的中点，证明：.【详解】连接,如图，由正方体知四边形是正方形，且M是的中点，所以， 即是的中点，又N是AC的中点，所以.题型二、证明线面平行2．如图，在四棱锥P-ABCD中，PC⊥平面ABCD，PC＝2，在四边形ABCD中，∠B＝∠C＝90°，AB＝4，CD＝1，点M在PB上，PB＝4PM，PB与平面ABCD成30°角.求证：CM∥平面PAD.【详解】证明：由题意知，CB，CD，CP两两垂直，以C为坐标原点，CB所在直线为x轴，CD所在直线为y轴，CP所在直线为z轴建立如图所示的空间直角坐标系Cxyz.因为PC⊥平面ABCD，所以∠PBC为PB与平面ABCD所成的角，所以∠PBC＝30°.因为PC＝2，所以BC＝2，PB＝4，所以D(0,1,0)，B(2，0,0)，A(2，4,0)，P(0,0,2)，M，所以＝(0，－1,2)， ＝(2，3,0)， ＝.设＝(x，y，z)为平面PAD的一个法向量，由 得 取y＝2，得x＝－，z＝1，所以＝(－，2,1)是平面PAD的一个法向量.因为，所以，.又平面PAD，所以CM∥平面PAD.题型三、证明面面平行3．如图，在正方体中，点E，F，G，H，M，N分别是该正方体六个面的中心，求证：平面平面HMN．【详解】由题意知，建立如图空间直角坐标系，设正方体的棱长为2，则，得，所以，即，又平面HMN，平面HMN，所以平面HMN，平面HMN，又平面EFG，平面EFG，，所以平面EFG平面HMN.题型四、证明线线垂直4．如图，在正方体中，点E在BD上，且；点F在上，且．求证：（1）；（2）．【详解】（1）如图建立空间直角坐标系，令正方体的棱长为，则，，，因为，，所以，，所以，，所以，所以（2）由（1）可知，所以，所以题型五、证明线面垂直5．如图，在长方体中，，，E是CD的中点．求证：平面．【详解】如图建立空间直角坐标系，则，，，所以，，所以，，所以，，因为，平面．所以平面．题型六、证明面面垂直6．如图，PA⊥平面ABCD，四边形ABCD是正方形，PA＝AD＝2，M、N分别是AB、PC的中点．求证：平面MND⊥平面PCD；【详解】∵PA⊥平面ABCD，AB⊥AD，∴AB、AD、AP两两互相垂直，如图所示，分别以AB、AD、AP所在直线为x轴、y轴和z轴建立空间直角坐标系，可得A（0，0，0），B（2，0，0），C（2，2，0），D（0，2，0），P（0，0，2），M（1，0，0），N（1，1，1），∴（0，1，1），（﹣1，1，﹣1），（0，2，﹣2）设（x，y，z）是平面MND的一个法向量，可得，取y＝﹣1，得x＝﹣2，z＝1，∴（﹣2，﹣1，1）是平面MND的一个法向量，同理可得（0，1，1）是平面PCD的一个法向量，∵•2×0+（﹣1）×1+1×1＝0，∴，即平面MND的法向量与平面PCD的法向量互相垂直，可得平面MND⊥平面PCD.1．如图，在正方体中，点M，N分别在线段，上，且，，P为棱的中点．求证：．【详解】证明：．因为，，所以，，．又因为P为中点，所以，从而与为共线向量．因为直线MN与BP不重合，所以．2．已知正方体中，棱长为2a，M是棱的中点.求证：平面.【详解】以点D为原点，分别以､与的方向为x､y与z轴的正方向，建立空间直角坐标系.则､､､､､､､，M是棱的中点得，.设面的一个法向量为，，，则令，则.又，因为平面，所以平面.3．在直四棱柱ABCD－A1B1C1D1中，底面ABCD为等腰梯形，AB∥CD，AB＝4，BC＝CD＝2，AA1＝2，F是棱AB的中点.试用向量的方法证明：平面AA1D1D∥平面FCC1. 【详解】证明：因为AB＝4，BC＝CD＝2，F是棱AB的中点，所以BF＝BC＝CF，所以△BCF为正三角形.因为ABCD为等腰梯形，AB＝4，BC＝CD＝2，所以∠BAD＝∠ABC＝60°.取AF的中点M，连接DM，则DM⊥AB，所以DM⊥CD.以D为原点，DM为x轴，DC为y轴，DD1为z轴建立空间直角坐标系Dxyz，则D(0,0,0)，D1(0,0,2)，A(，－1,0)，F(，1,0)，C(0,2,0)，C1(0,2,2)，所以＝(0,0,2)，＝(，－1,0)，＝(，－1,0)，＝(0,0,2)，所以∥，∥，所以DD1∥CC1，DA∥CF，因为CC1，CF⊂平面FCC1，CC1∩CF＝C，DD1，DA平面FCC1，所以DD1∥平面FCC1，DA∥平面FCC1，又DD1∩DA＝D， DD1，DA⊂平面AA1D1D， 所以平面AA1D1D∥平面FCC1.4．如图，在正方体中，E，F分别是，的中点．求证：．【详解】不妨设正方体的棱长为1，建立如图所示的空间直角坐标系，则，，所以．又，，所以．所以．所以，即．5．如图，在正方体中，O是AC与BD的交点，M是的中点．求证：平面MBD．【详解】建立如图所示空间直角坐标系，设正方体的边长为，则，，，由于，所以平面.6．如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD＝DE＝2AB.求证：平面BCE⊥平面CDE.【详解】设AD＝DE＝2AB＝2a，以A为原点，分别以AC，AB所在直线为x轴，z轴，以过点A在平面内垂直于AC的直线为y轴，建立如图所示的空间直角坐标系A－xyz，则A(0，0，0)，C(2a，0，0)，B(0，0，a)，D(a，a，0)，E(a，a，2a)．所以＝(a，a，a)，＝(2a，0，－a)，＝(－a，a，0)，＝(0，0，－2a)．设平面BCE的法向量为＝(x1，y1，z1)，由＝0，＝0可得即令z1＝2，可得＝(1，－，2)．设平面CDE的法向量为＝(x2，y2，z2)，由＝0，＝0可得即令y2＝1，可得＝(，1，0)．因为＝1×＋1×(－)＋2×0＝0.所以，所以平面BCE⊥平面CDE.1．直线l的一个方向向量为，平面的一个法向量为，若，则实数（       ）A． B．1 C． D．【答案】A【详解】直线l的一个方向向量为，平面的一个法向量为，且，所以，所以.故选：A.2．若直线l的一个方向向量为，平面α的一个法向量为，则（　　）A．l∥α或l⊂α B．l⊥αC．l⊂α D．l与α斜交【答案】A【详解】直线的一个方向向量为，平面α的一个法向量为，，， 或，故选：A3．已知向量，分别是直线､的方向向量，若，则下列几组解中可能正确的是（       ）A．， B．， C．， D．，【答案】C【详解】由题意，即，代入各选项中的值计算，只有C满足．故选：C.4．若，分别为直线，的一个方向向量，则（       ）．A． B．与相交，但不垂直C． D．不能确定【答案】C【详解】由，，得，所以，即.故选：C.5．设是直线l的方向向量，是平面α的法向量，则（       ）A．l⊥α B．lα C．lα或l⊂α D．l⊥α或l⊂α【答案】C【详解】，，可知l∥α或l⊂α.. 故选：C.6．设α，β是不重合的两个平面，α，β的法向量分别为，l和m是不重合的两条直线，l，m的方向向量分别为，那么αβ的一个充分条件是（       ）A．l⊂α，m⊂β，且 B．l⊂α，m⊂β，且C．，且 D．，且【答案】C【详解】对于A，由线面垂直的性质可知，只要l⊂α，m⊂β，都有，并不能说明αβ，则A错误；对于B，若l⊂α，m⊂β，且，则平面α，β平行或者相交，则B错误；对于C，由，且可得，，则，则C正确；对于D，若，且，则平面α，β平行或者相交，则D错误；故选：C7．（多选）已知为直线l的方向向量，，分别为平面，的法向量（，不重合），下列结论正确的有（       ）A． B． C． D．【答案】AB【详解】因为平面，不重合，所以平面，的法向量平行（或垂直）等价于平面，平行（或垂直），所以AB正确，因为直线的方向量平行于平面的法向量等价于直线垂直于平面，所以C错误，因为直线的方向量垂直于平面的法向量等价于直线平行于平面或直线在平面内，所以D错误，故选：AB8．（多选）给定下列命题，其中正确的命题是（       ）A．若是平面的法向量，且向量是平面内的直线的方向向量，则B．若，分别是不重合的两平面的法向量，则C．若，分别是不重合的两平面的法向量，则D．若两个平面的法向量不垂直，则这两个平面一定不垂直【答案】ACD【详解】对于A选项，由线面垂直的定义若一条直线和一个平面内所有的直线都垂直，我们称直线和平面垂直，所以，∴，A正确；对于B选项，两平面平行，则它们的法向量平行，所以B错误；对于C选项，两平面平行，则它们的法向量平行，∴或∴，C正确；对于D选项，两平面垂直它们的法向量垂直，所以两个平面的法向量不垂直，则这两个平面一定不垂直，D正确.故选：ACD.9．若直线的方向向量为，平面的法向量为，则当直线与平面垂直时，_________．【答案】【详解】由题可知：//，则10．已知直线的方向向量为，平面的法向量为若，则实数的值为___________.【答案】【详解】由题意，直线的方向向量为，平面的法向量为，因为，可得，可得，解得.故答案为：.11．已知直线的方向向量为，且直线经过点和点，则___________，___________.【答案】          【详解】因为，所以，解得，.故答案为：-3；3.12．已知是直线的方向向量，是平面的法向量，如果，则________________【答案】6【详解】∵，∴，∴，∴．故答案为：6．13．若平面外的一条直线的方向向量是，平面的法向量为，则与的位置关系是_____.【答案】平行【详解】因为直线的方向向量是，平面的法向量为，所以，所以，所以直线与平面平行，即l∥β.故答案为：平行.14．已知平面的一个法向量为，直线的一个方向向量为，且平面，则______.【答案】【详解】因为平面，所以，则，解得.故答案为：15．若为平面的一个法向量，为平面的一个法向量，已知，则的值为__________．【答案】【详解】根据题意，若∥，则∥，∴，解得， ∴.故答案为：.16．设，分别是平面，的法向量．若，则______．【答案】5【详解】∵，则，∴．故答案为：517．已知＝（3，a+b，a﹣b）（a，b∈R）是直线l的方向向量，＝（1，2，3）是平面α的法向量，若l⊥α，则5a+b＝__．【答案】36【详解】∵l⊥α，∴，∴，解得，∴．故答案为：36．18．如图，已知点E，F分别是正方体ABCD－A1B1C1D1的棱AB，AA1的中点，点M，N分别是线段D1E，C1F上的点，则与平面ABCD垂直的直线MN有________条．【答案】1【详解】假设存在满足条件的直线MN，建立空间直角坐标系如图所示，不妨设正方体的棱长为2，则D1(2,0,2)，E(1,2,0)，设M(x，y，z)，eq \o(D1M,\s\up6(—→))＝meq \o(D1E,\s\up6(—→))(0≤m≤1)，所以(x－2，y，z－2)＝m(－1,2，－2)，x＝2－m，y＝2m，z＝2－2m，所以M(2－m，2m，2－2m)，同理，若设eq \o(C1N,\s\up6(—→))＝neq \o(C1F,\s\up6(—→))(0≤n≤1)，可得N(2n，2n，2－n)，eq \o(MN,\s\up6(→))＝(m＋2n－2,2n－2m，2m－n)，又因为MN⊥平面ABCD，eq \o(CD,\s\up6(→))＝(2,0,0)，eq \o(CB,\s\up6(→))＝(0,2,0)，所以eq \b\lc\{\rc\ (\a\vs4\al\co1(m＋2n－2＝0，,2n－2m＝0，))解得eq \b\lc\{\rc\ (\a\vs4\al\co1(m＝\f(2,3)，,n＝\f(2,3)，))即存在满足条件的直线MN，有且只有一条．19．如图所示，在正方体ABCD－A1B1C1D1中，E，F分别为DD1和BB1的中点.求证：四边形AEC1F是平行四边形.【详解】如下图，以点D为坐标原点建立如图所示的空间直角坐标系，不妨设正方体的棱长为1，则,所以,所以，所以，又因为,所以，所以四边形AEC1F是平行四边形.20．如图，在四面体ABCD中，E是的中点．直线AD上是否存在点F，使得？【详解】假设直线AD上存在点F使，设， ，因为E是的中点，所以，，若，则，即，所以，即，所以 ，此时显然不成立，所以不存在点F，使得.21．如图，已知在正方体ABCD－A1B1C1D1中，M，N，P分别是AD1，BD，B1C的中点，利用向量法证明：（1）MN∥平面CC1D1D；（2）平面MNP∥平面CC1D1D．【详解】（1）证明：以D为坐标原点，，，的方向分别为x，y，z轴的正方向，建立空间直角坐标系，设正方体的棱长为2，则A(2，0，0)，C(0，2，0)，D(0，0，0)，M(1，0，1)，N(1，1，0)，P(1，2，1).由正方体的性质，知AD⊥平面CC1D1D，所以＝(2，0，0)为平面CC1D1D的一个法向量.由于＝(0，1，－1)，则＝0×2＋1×0＋(－1)×0＝0，所以⊥.又MN⊄平面CC1D1D，所以MN∥平面CC1D1D.（2）证明：因为＝(2，0，0)为平面CC1D1D的一个法向量，由于＝(0，2，0)，＝(0，1，－1)，则，即＝(2，0，0)也是平面MNP的一个法向量，所以平面MNP∥平面CC1D1D.22．如图，在正方体中，点E在棱上，且，点F是棱上的一个动点．点F在什么位置时，平面，并说明理由.【详解】点F位于的三等分点（靠近D点）时，平面，理由如下：以A为坐标原点，分别以AB，AD，所在直线为x轴，y轴，z轴建立空间直角坐标系，设正方体棱长为，则，设，故 ，设平面的法向量为，则 ，令得：，所以，因为，令，解得：，所以当点F位于的三等分点（靠近D点）时，平面.23．如图，在四棱锥中，平面ABCD，底面四边形ABCD为直角梯形，，，，，Q为PD的中点．求证：．【详解】证明：由题意，在四棱锥中，平面ABCD，底面四边形ABCD为直角梯形，．以A为原点，，，的方向分别为x轴、y轴、z轴正方向，建立空间直角坐标系：则，，，，．因为Q为PD的中点，所以，所以，，所以，所以．24．如图，四面体ABCD的每条棱长都等于a，M，N分别是AB，CD的中点．求证：，．【详解】由题意可知，三个向量两两间的夹角为，因为M，N分别是AB，CD的中点，所以,则，所以，同理可证.25．如图，正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD，AB＝AD＝2，CD＝4，M为CE的中点．（1）求证：BM∥平面ADEF；（2）求证：BC⊥平面BDE；（3）证明：平面BCE⊥平面BDE.【详解】证明　∵平面ADEF⊥平面ABCD，平面ADEF∩平面ABCD＝AD，AD⊥ED，ED⊂平面ADEF，∴ED⊥平面ABCD.以D为坐标原点，分别为x轴，y轴，z轴的正方向建立如图所示的空间直角坐标系．则D(0，0，0)，A(2，0，0)，B(2，2，0)，C(0，4，0)，E(0，0，2)，F(2，0，2)．（1）∵M为EC的中点，∴M(0，2，1)，则，，，，故共面．又BM⊄平面ADEF，∴BM∥平面ADEF.（2），，，，∴BC⊥DB.又，∴BC⊥DE.又DE∩DB＝D，DB，DE⊂平面BDE，∴BC⊥平面BDE.（3）证明　由（2）知BC⊥平面BDE，又BC⊂平面BCE，∴平面BCE⊥平面BDE.26．在正三棱锥P­ABC中，三条侧棱两两互相垂直，PA＝PB＝PC＝3，G是△PAB的重心，E，F分别为BC，PB上的点，且BE∶EC＝PF∶FB＝1∶2. 求证：平面EFG⊥平面PBC.【详解】建立如图所示空间直角坐标系，则E(0，2，1)，F(0，1，0)，G(1，1，0)．所以＝(0，－1，－1)，＝(1，－1，－1)．设平面EFG的一个法向量是＝(x，y，z)，则有⊥，⊥.所以 令y＝1，得z＝－1，x＝0，即平面EFG的一个法向量＝(0，1，－1)．显然＝(3，0，0)是平面PBC的一个法向量．又·＝0，所以⊥，即平面PBC的法向量与平面EFG的法向量互相垂直，所以平面EFG⊥平面PBC.27．在棱长是2的正方体中，E，F分别为的中点.(1)求的长；(2)证明：平面；(3)证明：平面.【详解】(1)以D点为原点建立如图所示的空间直角坐标系，则，∵E，F分别为的中点，∴，∴.(2)∵，∴，又平面平面，∴平面.(3)，∵，∴，又，､平面，∴平面.28．如图，在多面体中，四边形是梯形，四边形为矩形，面，，，．(1)求证：平面；(2)点为线段的中点，求证面．【详解】(1)证明：如图，建立空间坐标系，则，，，，，面，，且，又，面，为面的法向量，，，又平面，平面．(2)证明：由（1）可知，，，，，，， 又，面．29．如图，在直三棱柱中，，，D为AB的中点．试用向量的方法证明：(1)；(2)平面．【详解】(1)建立如图所示空间直角坐标系，设，则，，所以.(2)，，设平面的法向量为，则，故可令，，所以平面.30．如图所示，在直三棱柱ABCA1B1C1中，AB⊥BC，AB＝BC＝2，BB1＝1，E为BB1的中点，证明：平面AEC1⊥平面AA1C1C.【详解】由题意得AB，BC，B1B两两垂直．以B为原点，BA，BC，BB1分别为x，y，z轴，建立如图所示的空间直角坐标系．则A(2，0，0)，A1(2，0，1)，C(0，2，0)，C1(0，2，1)，E，则＝(0，0，1)，＝(－2，2，0)，＝(－2，2，1)，＝.设平面AA1C1C的一个法向量为＝(x1，y1，z1)．则令x1＝1，得y1＝1.∴＝(1，1，0)．设平面AEC1的一个法向量为＝(x2，y2，z2)．则⇒令z2＝4，得x2＝1，y2＝－1.∴＝(1，－1，4)．∵＝1×1＋1×(－1)＋0×4＝0.∴，∴平面AEC1⊥平面AA1C1C.31．如图所示，在直四棱柱中，底面为等腰梯形，，，，，，，分别是棱，，的中点．求证：（1）直线平面；（2）平面平面．【详解】（1）因为，，是棱的中点，所以，则为正三角形．因为底面为等腰梯形，所以．取的中点，连接，则，所以．以为坐标原点，，，所在直线分别为轴、轴、轴，建立空间直角坐标系，如图所示，则，，，，，所以，，．设平面的法向量为，则，令，可得平面的一个法向量为，则，所以．又直线平面，所以直线平面．（2）因为，，，所以，．设平面的法向量为，则，令，可得平面的一个法向量为．由（1）知，所以，即，所以平面平面．32．如图，在正三棱柱中，，，分别是，上的点，且，，求证：平面平面．【详解】以A为坐标原点，建立如图所示的空间直角坐标系，不妨设，则，，，∴，．∵轴平面，∴可取平面的一个法向量为．设平面的法向量为，则，取，得为平面的一个法向量．∵，∴，∴平面平面．33．如图，在正方体中，为底面的中心，是的中点．在棱上是否存在一点，使得平面平面？若存在，指出点的位置；若不存在，请说明理由．【详解】当为的中点时，平面平面．证明如下：设符合题意．连接，，．以为坐标原点，建立如图所示的空间直角坐标系，设正方体的棱长为2，则，，，，，∴，，．设平面的法向量为，则，即，令，则，，∴平面的一个法向量为．若平面平面，则也是平面的一个法向量．∵，∴，∴，又，∴当为的中点时，平面平面．34．如图，在四棱锥中，底面是矩形，平面，分别是的中点，求证：（1）直线平面；（2）直线直线.（用向量方法）【详解】证明：如图，建立空间直角坐标系，设，则.（1），，又平面，平面，直线平面.（2），.35．如图，在四棱锥中，平面ABCD．，四边形ABCD满足，，，点M为PC的中点，求证：平面PAB．【详解】证明：因为平面ABCD，所以，．又，所以PA，AB，AD两两垂直．以A为坐标原点建立空间直角坐标系，如图所示：则，，，．因为点M为PC的中点，所以，故．又，，所以．所以，，为共面向量．又平面PAB，所以平面PAB．36．如图，在三棱锥中，三条侧棱，，两两垂直，且，是的重心，，分别为，上的点，且．（1）求证：平面平面；（2）求证：与直线与都垂直．【详解】证明：（1）如图．以为坐标原点，，，所在的直线分别为轴、轴、轴，建立空间直角坐标系．则，，，，，，，于是，．设平面的法向量是，则，∴，令，得．显然是平面的一个法向量．又，∴．∴平面平面．（2）由（1），知，，，∴，，∴，，∴与直线与都垂直．37．如图，在平行六面体中，，，求证：直线平面．【详解】证明：设，，，则为空间中的一个基底，且因为，，所以，．，，．．故是平面的法向量，故直线平面．