备战2024高考一轮复习数学（理） 第四章 三角函数与解三角形 第四节 三角函数的图象与性质课件PPT

这是一份备战2024高考一轮复习数学（理） 第四章 三角函数与解三角形 第四节 三角函数的图象与性质课件PPT，共40页。PPT课件主要包含了一“点”就过等内容，欢迎下载使用。

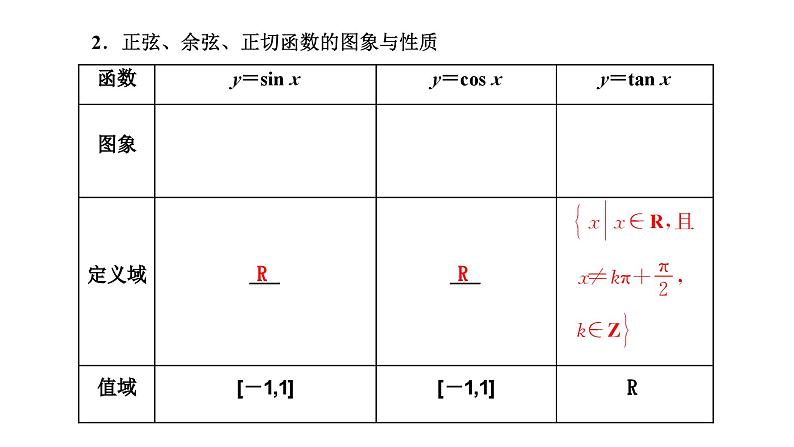
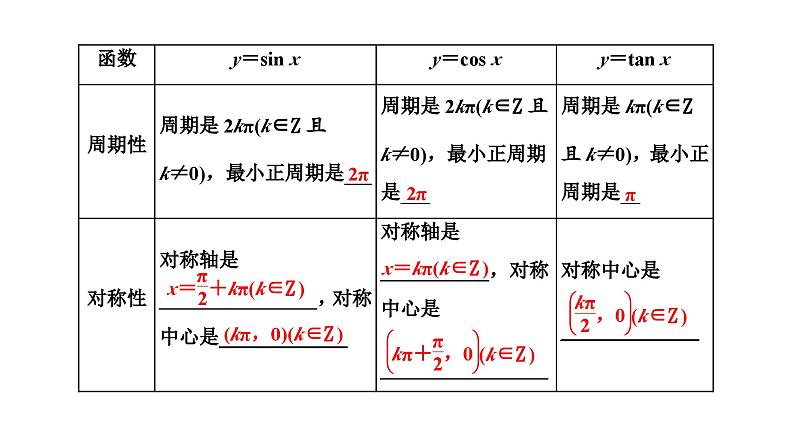
2．正弦、余弦、正切函数的图象与性质
1．函数y＝tan 2x的定义域是(　 )答案：D
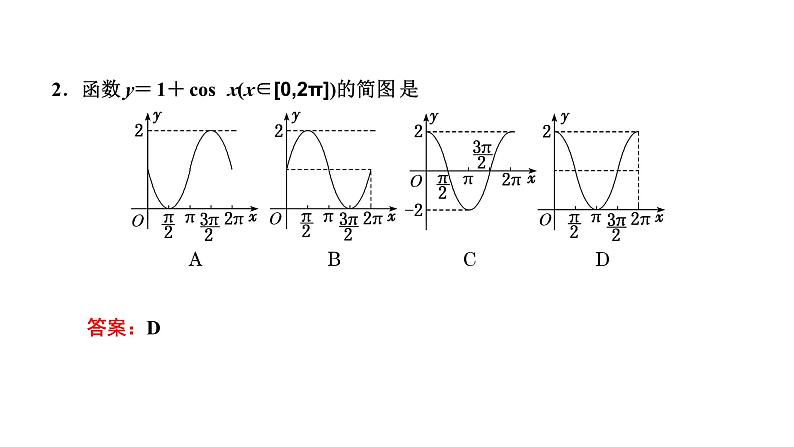
2．函数y＝1＋cs x(x∈[0,2π])的简图是(　 )答案：D
3．下列关系式中正确的是(　 )A．sin 11°＜cs 10°＜sin 168°B．sin 168°＜sin 11°＜cs 10°C．sin 11°＜sin 168°＜cs 10°D．cs 10°＜sin 168°＜sin 11°解析：sin 168°＝sin(180°－168°)＝sin 12°，cs 10°＝sin(90°－10°)＝sin 80°，∴sin 11°＜sin 12°＜sin 80°，即sin 11°＜sin 168°＜cs 10°.答案：C　
5．若函数y＝cs(x＋φ)为奇函数，则最小的正数φ＝________.
4．若函数f(x)＝sin(x＋φ)＋cs x的最大值为2，则常数φ的一个取值为_______．
[一“点”就过]求解三角函数的值域(最值)的常见类型(1)形如y＝asin x＋bcs x＋c的三角函数化为y＝Asin(ωx＋φ)＋c的形式，再求值域(最值)．(2)形如y＝asin2x＋bsin x＋c的三角函数，可先设sin x＝t，化为关于t的二次函数求值域(最值)．(3)形如y＝asin xcs x＋b(sin x±cs x)＋c的三角函数，可先设t＝sin x±cs x，化为关于t的二次函数求值域(最值)．
[方法技巧]1．求三角函数单调区间的2种方法(1)代换法：就是将比较复杂的三角函数中含自变量的代数式整体当作一个角u(或t)，利用复合函数的单调性列不等式求解．(2)图象法：画出三角函数的图象，结合图象求它的单调区间．2．已知三角函数的单调区间求参数范围的3种方法(1)求出原函数的相应单调区间，由所给区间是所求某区间的子集，列不等式(组)求解．(2)由所给区间求出整体角的范围，由该范围是某相应正、余弦函数的某个单调区间的子集，列不等式(组)求解．
层级三/ 细微点——优化完善(扫盲点)1．(链接生活实际)人的心脏跳动时，血压在增加或减少．血压的最大值、最小值分别为收缩压和舒张压，收缩压120 mmHg，舒张压80 mmHg为血压的标准值．设某人的血压满足函数式p(t)＝102＋24sin 160πt，其中p(t)为血压(单位：mmHg)，t为时间(单位：min)，则下列说法正确的是(　 )A．收缩压和舒张压均高于相应的标准值B．收缩压和舒张压均低于相应的标准值C．收缩压高于标准值、舒张压低于标准值D．收缩压低于标准值、舒张压高于标准值解析：因为p(t)＝102＋24sin 160πt，且－1≤sin 160πt≤1，所以p(t)∈[78,126]，即收缩压为126 mmHg，舒张压为78 mmHg.因为120＜126,80＞78，所以C正确．答案：C　
4．(逆向思维)(1＋tan 1°)·(1＋tan 2°)·(1＋tan 3°)·…·(1＋tan 44°)·(1＋tan 45°)的值是________．解析：若A＋B＝45°，则(1＋tan A)(1＋tan B)＝1＋tan A＋tan B＋tan Atan B＝1＋tan(A＋B)(1－tan Atan B)＋tan Atan B＝2，所以原式＝[(1＋tan 1°)(1＋tan 44°)]·[(1＋tan 2°)(1＋tan 43°)]·…·[(1＋tan 22°)(1＋tan 23°)]·(1＋tan 45°)＝223.答案：223
“课时验收评价”见“课时验收评价(二十五)” (单击进入电子文档)