专题08 焦长与焦比体系之双曲线-高考数学满分突破之解析几何篇
展开专题08 焦长与焦比体系之双曲线
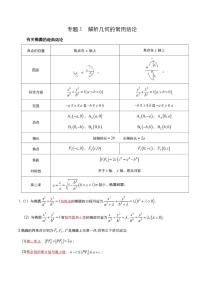
周长问题:双曲线(,)的两个焦点为、,弦过左焦点(、都在左支上),,则的周长为(如下图左)
焦长公式:(1)当AB交双曲线于一支时,,(图中)
(2)当AB交双曲线于两支时,,(图右)
双曲线焦比定理和椭圆的焦比定理一致:
令,即,代入弦长公式可得.
若交于两支时,,代入弦长公式可得.
例1.(1)、(2021·全国)已知,为双曲线的左、右焦点,斜率为的直线过分别交双曲线左、右支于、点,,则双曲线的渐近线方程为( )
A. B.
C. D.
【答案】D
【解析】
【分析】
设,由双曲线定义得:,,作,利用勾股定理求得参数关系,结合渐近线公式即可求解.
【详解】
设,由双曲线定义得:,,
所以,
作,△中,设直线的倾斜角为,则,可得,
△中,勾股定理得:①,
△中,勾股定理得:,
可得②,
由①②可得,整理可得,即可得.
所以渐近线的斜率为,故渐近线方程为.
故选:D.
(2)、(2021·天津·统考高考真题)已知双曲线的右焦点与抛物线的焦点重合,抛物线的准线交双曲线于A,B两点,交双曲线的渐近线于C、D两点,若.则双曲线的离心率为( )
A. B. C.2 D.3
【答案】A
【分析】设公共焦点为,进而可得准线为,代入双曲线及渐近线方程,结合线段长度比值可得,再由双曲线离心率公式即可得解.
【详解】设双曲线与抛物线的公共焦点为,
则抛物线的准线为,
令,则,解得,所以,
又因为双曲线的渐近线方程为,所以,
所以,即,所以,
所以双曲线的离心率.
故选:A.
【变式训练1-1】、(2019·陕西榆林·校联考一模)如图所示,,是双曲线:的左、右焦点,过的直线与的左、右两支分别交于A,两点.若,则双曲线的离心率为( )
A.
B.
C.
D.
【答案】C
【分析】不妨令,,,根据双曲线的定义可求得,,再利用勾股定理可求得,从而可求得双曲线的离心率.
【详解】,不妨令,,,
,,
又由双曲线的定义得:,,
,
,.
在中,,
又,,
双曲线的离心率.
故选;C
【变式训练1-2】、(2022·天津河西·统考一模)已知双曲线的左、右焦点分别为、,c是双曲线C的半焦距,点A是圆上一点,线段交双曲线C的右支于点B,,,则双曲线C的离心率为( ).
A. B. C. D.
【答案】A
【分析】根据已知及双曲线的定义,可把用a表示,再用勾股定理推出,在中,利用勾股定理建立a,c的关系式即可求出离心率.
【详解】如下图,由题意可知,由双曲线定义可知,
易得,由勾股定理可得,在中,再由勾股定理得,所以.
故选:A.
例2.(1)、(2022·安徽·高二开学考试)已知双曲线的左、右焦点分别为,,过的直线交双曲线C的左支于P,Q两点,若且的周长为,则双曲线C的离心率为___________.
【答案】##
【解析】
【分析】
由所给的条件,利用双曲线的定义即可.
【详解】
由双曲线定义知,
则,,
所以,
∴的周长为,
∴……①,,
由,得
∴……②,
由①②:
∴,,∴,
在中,,
.
故答案为: .
(2)、(2022·江西南昌·统考二模)已知、分别是双曲线的左、右焦点,也是抛物线的焦点,点是双曲线与抛物线的一个公共点,若,则双曲线的离心率为___________.
【答案】##
【分析】过点作抛物线准线的垂线,垂足为点,求出,求出、的余弦值,由题意可知,可得出关于、的齐次等式,结合可解得的值.
【详解】过点作抛物线准线的垂线,垂足为点,则,
因为,则,则,
因为,则,
由余弦定理可得,
因为,所以,,所以,,
整理可得,即,因为,解得.
故答案为:.
(3)、(2022·陕西·统考二模)已知椭圆,双曲线的离心率互为倒数,,为双曲线的左、右焦点,设点M为的渐近线上的一点,若(O为坐标原点),的面积为16,则的方程为___________.
【答案】
【分析】根据椭圆的离心率求得双曲线的离心率,从而求得双曲线渐近线的方程,根据以及的面积列方程,化简求得,从而求得的方程.
【详解】椭圆的离心率为,
所以双曲线的离心率为,
不妨设在直线上,设,则,设,,
则,
∵,∴.整理得①,
依题意:,即:②,
①②联立得.
∴,,,
∴的方程为:.
故答案为:
【变式训练2-1】、(2022·广东汕头·一模)已知双曲线,,为C的两条渐近线,过C的右焦点F作的垂线,垂足为A,且该垂线交于点B,若,则曲线C的离心率______.
【答案】##
【解析】
【分析】
不妨设为,为,则直线的方程为,联立联立,求得点的坐标,联立,求得点的坐标,再根据,得出的齐次式,从而可得出答案.
【详解】
解:不妨设为,为,
过C的右焦点F作的垂线,垂足为A,且该垂线交于点B,
,则直线的方程为,
联立,解得,
即,
联立,解得,
即,
则,,
因为,
所以,
所以,即,
所以,所以,
所以.
故答案为:.
【变式训练2-2】、(2022·河北·模拟预测)已知双曲线的左、右焦点分别为,直线在第一象限交双曲线C右支于点A.若双曲线的离心率满足,且,则k的取值范围是___________.
【答案】
【解析】
【分析】
由双曲线的定义结合勾股定理得出,再由等面积法得出,,再由结合离心率公式以及范围得出k的取值范围.
【详解】
设,由题可知,∴.
∴,∴,∴.
又由,可知,∴,解得.
∵,,∴.
∴,依题意,,∴.
故答案为:
【变式训练2-3】、(2022·浙江新昌·高三期末)梯形中,,线段交以,为焦点且过,的双曲线于点,若,则双曲线的离心率为_____.
【答案】
【解析】
【分析】
设,双曲线为,求坐标,应用定比分点求坐标,将代入双曲线方程得到齐次方程求离心率即可.
【详解】
由题设,如下图示,令双曲线为,
由,则,
令,可得,故,又,
则,,
所以,由E在双曲线上,可得,整理得,且,则.
故答案为:.
例3.(2022·全国·模拟预测)已知双曲线的焦点在轴上,中心在原点,离心率为,且过点.
(1)求双曲线的标准方程;
(2)双曲线的左右顶点为,,且动点,在双曲线上,直线与直线交于点,,,求的取值范围.
【答案】(1);
(2).
【解析】
【分析】
(1)利用离心率,点在双曲线上以及,,的关系,联立方程即可求得,的值,从而求得双曲线的标准方程;
(2)将直线和直线的方程分别用点斜式表示出来,并联立求得点的轨迹方程,易知,再由点的轨迹方程,可知的范围,从而求解.
(1)
解:设双曲线的标准方程为,
联立得,,所以双曲线的标准方程为.
(2)
解:已知,,,.
当时,动点与点,重合,
当时,直线,直线,
联立两直线方程得.
又因为,即,所以,即.
又,
且,所以.
例4、(2022·河南·襄城县教育体育局教学研究室二模(理))已知双曲线的右焦点为,过点F与x轴垂直的直线与双曲线C交于M,N两点,且.
(1)求C的方程;
(2)过点的直线与双曲线C的左、右两支分别交于D,E两点,与双曲线C的两条渐近线分别交于G,H两点,若,求实数的取值范围.
【答案】(1)
(2)
【解析】
【分析】
(1)根据双曲线右焦点为,且,由求解;
(2)设直线的方程为,与双曲线方程联立,求得,与双曲线C的渐近线方程联立,求得,根据求解.
(1)
解:由题意得,
解得
故C的方程为.
(2)
显然直线率存在,设直线的方程为,,,
联立,得,
因为与双曲线C的左,右两支分别交于D,E两点,
故,
解得,
此时有.
,
,
由,解得,同理可得,
所以.
因为,故.
因为,故,
故实数的取值范围是.
例5、(2022·福建漳州·统考一模)已知双曲线的左、右焦点分别为,,点是右支上一点,若I为的内心,且.
(1)求的方程;
(2)点A是在第一象限的渐近线上的一点,且轴,在点P处的切线l与直线相交于点M,与直线相交于点N.证明:无论点P怎么变动,总有.
【答案】(1);
(2)证明见解析.
【分析】(1)根据三角形面积公式及双曲线定义化简可得,求出即可得出方程;
(2)利用导数的几何意义求出切线斜率并化简可得,求出切线及切线与直线的交点,利用两点间距离公式并结合双曲线方程化简可得.
(1)
设的内切圆半径为r,
则,
因为,
所以,
即,可得,
所以,
由双曲线的定义和几何性质,得,
又,解得,
所以的方程为.
(2)
由题意可知,直线l的斜率存在,设直线l的方程为.
由可得
由题意知.
若点P在双曲线右支的上半支上,则
所以,故
因为, 所以,
若点P在双曲线右支的下半支上,则
同理可得
综上,,代入直线l的方程得,
即,
由,可得,
所以直线l的方程为, 即
因为直线的方程为x=2,
所以直线l与直线的交点,
直线l与直线的交点
所以,
,
即得证.
例6、(2022·安徽六安·安徽省舒城中学校考一模)椭圆:的焦点,是等轴双曲线:的顶点,若椭圆与双曲线的一个交点是P,的周长为.
(1)求椭圆的标准方程;
(2)过点任作一动直线交椭圆与两点,记,若在直线上取一点,使得,试判断当直线运动时,点是否在某一定直线上运动?若是,求出该直线的方程;若不是,请说明理由.
【答案】(1)
(2)是,
【分析】(1)由题知,进而根据焦点三角形的知识得,进而得,即可求得答案;
(2)根据题意,设直线的方程为,,进而与椭圆联立方程,结合韦达定理与向量坐标运算得,再根据得,进而得答案.
(1)
解:由题可知:,所以,
因为的周长为,
所以,即,
所以,
所以椭圆的方程为;
(2)
解:依题可知:直线的斜率存在,设方程为,,
所以,
所以,,
由,
设,由,
所以,
所以.
所以点是在直线上运动.
1.(2022·江西·模拟预测(文))如图,已知双曲线的右焦点为F,以原点为圆心,焦距为直径的圆交双曲线于A,B两点,线段经过右焦点F,若,则该双曲线的渐近线方程为( )
A. B. C. D.
【答案】D
【解析】
【分析】
记左焦点为,连接,由双曲线的对称性得,由得,然后由双曲线的定义和直角三角形、直角三角形建立的关系式求得渐近线方程.
【详解】
如图,记左焦点为,连接,由双曲线的对称性得,
由得,
设,则,
又,即,从而由得
,,,
从而,
所以,化简得,所以,
渐近线方程为.
故选:D.
2.(2021·全国·统考高考真题)已知是双曲线C的两个焦点,P为C上一点,且,则C的离心率为( )
A. B. C. D.
【答案】A
【分析】根据双曲线的定义及条件,表示出,结合余弦定理可得答案.
【详解】因为,由双曲线的定义可得,
所以,;
因为,由余弦定理可得,
整理可得,所以,即.
故选:A
【点睛】关键点睛:双曲线的定义是入手点,利用余弦定理建立间的等量关系是求解的关键.
3.(2022·黑龙江·铁人中学高二开学考试)已知点,分别为双曲线的左,右焦点,M为C的左支上一点,,若圆与直线相切,则C的离心率为( )
A. B. C. D.
【答案】A
【解析】
【分析】
根据直线与圆相切可得等腰三角形底边上的高,再结合双曲线的定义可得的关系式,从而可求双曲线的离心率.
【详解】
作,垂足为,
因为圆与直线相切,故.
因为,所以,而,
故三角形为等腰三角形,故,
又,即,所以,即.
故选:A.
4.(2022·吉林·长春外国语学校高三开学考试(文))已知双曲线的左、右焦点分别为,两条渐近线的夹角为,过点作轴的垂线,交双曲线的左支于两点,若的面积为,则该双曲线的方程为( )
A. B.
C. D.
【答案】D
【解析】
【分析】
根据渐近线夹角和可确定,结合三角形面积、双曲线关系可构造方程组求得,由此可得双曲线方程.
【详解】
为双曲线的通径,,又,
;
两条渐近线的夹角为,渐近线的倾斜角为或,
又,,渐近线倾斜角为,即;
由得:,双曲线方程为:.
故选:D.
5.(2022·内蒙古·赤峰二中高二期末(理))已知直线:与双曲线的两条渐近线分别相交于A、B两点,若C为直线与y轴的交点,且,则k等于( )
A.4 B.6 C. D.
【答案】D
【解析】
【分析】
先求出双曲线的渐近线方程,然后分别与直线联立,求出A、B两点的横坐标,再利用可求解.
【详解】
由双曲线方程可知其渐近线方程为:,
当时,与联立,得,
同理得,
由,且可知,
所以有,解得.
故选:D
6.(2022·河南·驻马店市基础教学研究室高二期末(理))设,为双曲线的上,下两个焦点,过的直线l交该双曲线的下支于A,B两点,且满足,,则双曲线的离心率为( )
A. B. C. D.
【答案】A
【解析】
【分析】
设,表示出,由勾股定理列式计算得,然后在,再由勾股定理列式,计算离心率.
【详解】
由题意得,,且,如图所示,
设,由双曲线的定义可得,,因为,所以,得,所以,在中,,即.
故选:A
【点睛】
双曲线的离心率是双曲线最重要的几何性质,求双曲线的离心率(或离心率的取值范围),常见有两种方法:
求出,代入公式;
②只需要根据一个条件得到关于的齐次式,结合转化为的齐次式,然后等式(不等式)两边分别除以或转化为关于的方程(不等式),解方程(不等式)即可得 (的取值范围).
7.(2021·天津津南·天津市咸水沽第一中学校考模拟预测)设,是双曲线()的左、右焦点,是坐标原点.过作的一条渐近线的垂线,垂足为.若,则的离心率为
A. B. C. D.
【答案】B
【详解】分析:由双曲线性质得到,然后在和在中利用余弦定理可得.
详解:由题可知
在中,
在中,
故选B.
点睛:本题主要考查双曲线的相关知识,考查了双曲线的离心率和余弦定理的应用,属于中档题.
8.(2021·四川成都·石室中学统考一模)已知双曲线的左、右焦点分别为,,过的直线l交双曲线C的渐近线于A,B两点,若,(表示的面积),则双曲线C的离心率的值为( )
A. B. C. D.或
【答案】D
【分析】以直线斜率是否存在进行分类.斜率存在时,直接代入题设中的式子,求出的值,进而求出离心率.斜率不存在时,由题意得出点的轨迹为圆,再利用解出点的坐标,根据“点差法”求出,进而求出离心率即可.
【详解】若直线斜率不存在,不妨设点,
则
所以,则离心率;
若直线斜率存在,设,
中点,不妨设M在x轴上方,
由,得,
故点M在圆上,
由,得,
则,所以.
由得,即.
当时,,得.
当时,,矛盾,舍去.
综上所述,或.
故选:D.
【点睛】关键点点睛:本题是求双曲线的离心率,在直线斜率不存在时,利用两点的中点,采用“点差法”求出是解题的关键.
9.(2022·山东临沂·一模)已知,分别为双曲线C:(,)的左,右焦点,点P在第二象限内,且满足,,线段与双曲线C交于点Q,若.则C的离心率为( )
A. B. C. D.
【答案】C
【解析】
【分析】
取的中点,由已知得,由三线合一得△是等腰三角形,表示出各边长,再由余弦定理表示,再由双曲线的定义表示,在△中由余弦定理列式,得关于的等式关系,即可求得离心率.
【详解】
取线段的中点,连接,
因为,所以,
所以△是等腰三角形,且,
在中,,
连接,又,点在双曲线上,由,则,
在△中,,整理得,
所以离心率.
故选:C
10.(2022·江西·南昌市实验中学高二阶段练习(理))如图所示,双曲线:的左、右焦点分别为、,过的直线与双曲线 C 的两条渐近线分别交于A、B两点,A是的中点,且,则双曲线C的离心率( )
A. B.2 C. D.
【答案】B
【解析】
【分析】
由已知可得,设,,,,由点在渐近线上,求得点坐标,再由为的中点,得到点坐标,把代入渐近线,即可求得的离心率.
【详解】
A是的中点,
为△的中位线,
,所以,所以.
设,,,,
点在渐近线上,
,得.
又为的中点,,
在渐近线上,
,得,则双曲线的离心率.
故选:B
11.(2022·福建漳州·高二期末)已知双曲线的左、右焦点分别为,,过点作直线交双曲线的右支于A,B两点.若,则双曲线的离心率为( )
A. B. C. D.
【答案】A
【解析】
【分析】
根据给定条件结合双曲线定义求出,,再借助余弦定理求出半焦距c即可计算作答.
【详解】
因,令,,而双曲线实半轴长,
由双曲线定义知,,
而,于是可得,在等腰中,,
令双曲线半焦距为c,在中,由余弦定理得:,
而,,,解得,
所以双曲线的离心率为.
故选:A
【点睛】
方法点睛:求双曲线的离心率的方法:
(1)定义法:通过已知条件列出方程组,求得得值,根据离心率的定义求解离心率 ;
(2)齐次式法:由已知条件得出关于 的二元齐次方程,然后转化为关于 的一元二次方程求解;
(3)特殊值法:通过取特殊值或特殊位置,求出离心率.
12.(2022·浙江上虞·高二期末)过双曲线右焦点F作双曲线一条渐近线的垂线,垂足为A,与另一条渐近线交于点B,若,则双曲线C的离心率为( )
A.或 B.2或 C.或 D.2或
【答案】A
【解析】
【分析】
分A,B在x轴上方和下方两种情况,联立直线方程,分别求得点A,B的坐标,利用求解.
【详解】
如图所示:
当A,B在x轴上方时,由题意得,解得,
即;
由得,即,
因为,
所以,
解得,则,
如图所示:
当A,B在x轴下方时,由题意得,解得,
即;
由,得,即,
因为,
所以,
解得,则,
故选:A
13.(2022·江西南昌·高二期末(理))设双曲线:的左、右焦点分别为、,P为C上一点,且,,则双曲线的渐近线方程为( )
A. B. C. D.
【答案】B
【解析】
【分析】
根据双曲线的定义结合,求得,在中,利用余弦定理求得之间的关系,即可得出答案.
【详解】
解:因为在双曲线中,因为,
所以,
所以,
在中,,,
由余弦定理可得,
即,所以,
所以,
所以,
所以双曲线的渐近线方程为.
故选:B.
14.(2022·河南·沈丘县第一高级中学高二期末(理))已知双曲线(,)的左、右焦点分别为,,点A的坐标为,点P是双曲线在第二象限的部分上一点,且,点Q是线段的中点,且,Q关于直线PA对称,则双曲线的离心率为( )
A.3 B.2
C. D.
【答案】C
【解析】
【分析】
由角平分线的性质可得,结合已知条件即可求双曲线的离心率.
【详解】
由题设,易知:,
由知:,即,整理得:.
故选:C
15.(2022·陕西·武功县普集高级中学一模(理))如图所示,已知是双曲线的右焦点,是坐标原点,是条渐近线,在上分别有点(不同于坐标原点 ),若四边形为菱形,且其面积为.则双曲线的离心率为( )
A.3 B.2 C. D.
【答案】B
【解析】
【分析】
根据菱形的面积可知,再根据勾股定理可得,即,进而求出,根据渐近线的斜率,可得,再利用离心率,即可求出结果.
【详解】
由四边形为菱形,则,
所以菱形的面积为
所以,
又,
所以,即,
又点分别是渐近线上的点,
所以渐近线的斜率,
故双曲线的离心率为.
故选:B.
16.(2022·广西·统考模拟预测)如图所示,已知双曲线:的右焦点为,双曲线的右支上一点,它关于原点的对称点为,满足,且,则双曲线的离心率是______.
【答案】
【分析】连接左焦点,得到平行四边形,通过余弦定理列方程即可解出.
【详解】
设双曲线的左焦点为,连接,,根据双曲线的对称性可知,
四边形为平行四边形,由题意以及双曲线定义,
可得,
则,,,
所以,
即,即,
所以双曲线的离心率为:.
故答案为:.
17.(2022·安徽·芜湖一中一模(理))设,分别是双曲线的左、右焦点,是右支上一点.若,点到直线的距离为,则的离心率为__________________.
【答案】
【解析】
【分析】
利用双曲线的定义,构造齐次式,进而可得离心率.
【详解】
如图所示,由已知得,且,,
则
又由双曲线定义可知,即,而,
可得,即,
所以的离心,
故答案为:.
18.(2022·全国·高三专题练习)已知椭圆与双曲线有公共的左、右焦点、,它们在第一象限交于点,其离心率分别为、,以、为直径的圆恰好过点,则_____.
【答案】2
【解析】
【分析】
根据椭圆与双曲线的定义列方程组,再由圆的性质可得齐次式,然后可得.
【详解】
椭圆与双曲线有公共的左、右焦点、,
由题意可知,以、为直径的圆恰好过点P,所以
又,,,
,,即.
故答案为:2.
19.(2022·广东广州·统考一模)设双曲线的左、右焦点分别为、,过点的直线分别与双曲线的左、右支交于点、,若以为直径的圆过点,且,则该双曲线的离心率为______.
【答案】
【分析】先根据题意,判断出△为等腰直角三角形,找到,在△中,利用余弦定理建立关于a、c的齐次式,求出离心率e.
【详解】
因为以为直径的圆过点,所以,又,所以△为等腰直角三角形,所以.
设,则由双曲线的定义可得:,两式相加得:,即.所以,解得:.
在△中,,,,
由余弦定理得:,
即,整理化简得:
.
故答案为:.
【点睛】求椭圆(双曲线)离心率的一般思路:
(1)直接求出a、b、c,计算离心率;
(2)根据题目的条件,找到a、b、c的关系,消去b,构造离心率e的方程或(不等式)即可求出离心率.
20.(2022·广西岑溪·高二期末(理))已知双曲线的左,右焦点分别为,P是该双曲线右支上一点,且(O为坐标原点),,则双曲线C的离心率为__________.
【答案】
【解析】
【分析】
由已知及向量数量积的几何意义易知,根据双曲线的性质可得,再由双曲线的定义及勾股定理构造关于双曲线参数的齐次方程求离心率.
【详解】
∵,
∴△为等腰三角形且,又,
∴,
∴.又,,
∴,则,可得,
∴双曲线C的离心率为.
故答案为:.
21.(2022·重庆沙坪坝·重庆南开中学校考模拟预测)已知,直线过椭圆的右焦点F且与椭圆交于A、B两点,l与双曲线的两条渐近线、分别交于M、N两点.
(1)若,且当轴时,△MON的面积为,求双曲线的方程;
(2)如图所示,若椭圆的离心率,且,求实数的值.
【答案】(1);
(2).
【分析】(1)由题设可得、,结合三角形面积可得,由椭圆参数关系求a、b,即可写出双曲线方程.
(2)由椭圆离心率可得,进而可得双曲线渐近线,假设,写出、l方程,联立求N坐标,由向量的数量关系及向量坐标表示求A坐标,根据A在椭圆上求值.
【详解】(1)由题设,且双曲线的渐近线为,
当轴时,,又,△MON的面积为,
所以,故,而,可得,
所以双曲线的方程为.
(2)对于椭圆有,而,则,
不妨假设,则且l为,
所以,又,,
令,则,故,
所以,而在椭圆上,
则,整理得,
综上,可得.
22.(2022·山东潍坊·统考模拟预测)已知双曲线的左、右焦点分别为、,双曲线的右顶点在圆上,且.
(1)求双曲线的方程;
(2)动直线与双曲线恰有1个公共点,且与双曲线的两条渐近线分别交于点、,设为坐标原点.求证:的面积为定值.
【答案】(1)
(2)证明见解析
【分析】(1)设,通过,求解,通过在圆上,求解,得到双曲线的标准方程.
(2)当动直线的斜率不存在时,求解三角形的面积;当动直线的斜率存在时,且斜率,不妨设直线,联立直线与双曲线方程,求出,然后求解的坐标,求解,结合原点到直线的距离,求解的面积是为定值即可.
【详解】(1)不妨设 , 因为,
从而 故由 ,
又因为, 所以 ,
又因为 在圆 上, 所以
所以双曲线的标准方程为:
(2)设直线与轴交于点,双曲线的渐近线方程为
由于动直线与双曲线恰有1个公共点, 且与双曲线的两条渐近线分别交于点,
当动直线的斜率不存在时, ,,,
当动直线的斜率存在时, 且斜率, 不妨设直线 ,
故由
依题意,且
,
化简得 ,
故由 ,
同理可求,,
所以
又因为原点到直线的距离,
所以,又由
所以,
故的面积是为定值,定值为
23.(2021·全国·模拟预测)双曲线C:(a>0,b>0)的左顶点为A,右焦点为F,动点B在C上,当BF⊥AF时,|AF|=|BF|.
(1)求C的离心率;
(2)若B在第一象限,证明:∠BFA=2∠BAF.
【答案】(1)2;
(2)证明见解析.
【分析】(1)运用代入法,结合双曲线的离心率公式进行求解即可;
(2)根据直线斜率公式,结合二倍角的正切公式进行证明即可.
(1)
设双曲线的离心率为e,焦距为2c,,
在中令x=c,则,解得,若|AF|=|BF|,则,
所以a2+ac=b2=c2-a2,所以e2-e-2=0,解得e=2或(舍去),所以e=2;
(2)
因为e=2,所以,
所以,,设B(x,y)(x>0,y>0),
kAB=,kBF=,设∠BAF=θ,则tan θ=,
tan2θ========-kBF=tan∠BFA,所以∠BFA=2∠BAF.
【点睛】关键点睛:利用二倍角的正切公式是解题的关键.
24.(2022·浙江宁波·统考一模)已知点,在双曲线E:上.
(1)求双曲线E的方程;
(2)直线l与双曲线E交于M,N两个不同的点(异于A,B),过M作x轴的垂线分别交直线AB,直线AN于点P,Q,当时,证明:直线l过定点.
【答案】(1)
(2)证明见解析
【分析】(1)将点坐标代入双曲线方程,即可求解的值,进而得双曲线方程;
(2)设直线方程,联立直线与双曲线方程,得到韦达定理,根据向量关系,转化为坐标关系,即可得的关系,进而可得直线过定点.
【详解】(1)由题知, ,得,
所以双曲线E的方程为.
(2)由题意知,当l⊥x轴时,与重合,由可知:是的中点,显然不符合题意,
故l的斜率存在,设l的方程为,
联立,消去y得,则
,即,且,
设,,,,
AB方程为,令,得,
AN方程为,令得,
由,得,即,
即,
即,
将,代入得
即,
所以,
得或,
当,此时由,得,符合题意;
当,此时直线l经过点A,与题意不符,
舍去所以l的方程为,即,
所以l过定点.
25.(2022·河南许昌·统考二模)已知双曲线的右焦点为,过点F与x轴垂直的直线与双曲线C交于M,N两点,且.
(1)求C的方程;
(2)过点的直线与双曲线C的左、右两支分别交于D,E两点,与双曲线C的两条渐近线分别交于G,H两点,若,求实数的取值范围.
【答案】(1)
(2)
【分析】(1)根据双曲线右焦点为,且,由求解;
(2)设直线的方程为,与双曲线方程联立,求得,与双曲线C的渐近线方程联立,求得,根据求解.
【详解】(1)解:由题意得,
解得
故C的方程为.
(2)显然直线率存在,设直线的方程为,,,
联立,得,
因为与双曲线C的左,右两支分别交于D,E两点,
故,
解得,
此时有.
,
,
由,解得,同理可得,
所以.
因为,故.
因为,故,
故实数的取值范围是.
26.(2022·上海普陀·统考二模)设分别是双曲线的左、右两焦点,过点的直线与的右支交于M,N两点,过点(﹣2,3),且它的虚轴的端点与焦点的距离为.
(1)求双曲线的方程;
(2)当时,求实数m的值;
(3)设点M关于坐标原点O的对称点为P,当时,求△PMN面积S的值.
【答案】(1)
(2)
(3)
【分析】(1)根据点在双曲线上及两点距离列方程组求双曲线参数,即可得方程;
(2)由点在直线上求得t=2,根据F1到直线的距离与等腰三角形底边上的高相等,列方程求参数m;
(3)设M(x1,y1),N(x2,y2),联立双曲线与直线方程,应用韦达定理得,,由向量的数量关系可得,根据对称点,三角形面积公式,可求△PMN面积.
【详解】(1)因为双曲线过点(﹣2,3),且它的虚轴的端点与焦点的距离为,
可得:,解得:,
所以双曲线的方程为.
(2)因为直线,且过点F2(2,0),
则,解得:,
由得:三角形为等腰三角形,
所以等腰三角形底边上的高的大小为,
又因为点F1到直线的距离等于等腰三角形底边上的高,
则,
化简得:,即.
(3)设M(x1,y1),N(x2,y2),
由直线与双曲线联立得:,
化简得:,
由韦达定理得:,,
又,即,则,,
即,则,
又点M关于坐标原点O的对称点为P,则:
.
则所求的△PMN面积为.
专题09 焦长与焦比体系之抛物线-高考数学满分突破之解析几何篇: 这是一份专题09 焦长与焦比体系之抛物线-高考数学满分突破之解析几何篇,文件包含专题09焦长与焦比体系之抛物线教师版docx、专题09焦长与焦比体系之抛物线学生版docx等2份试卷配套教学资源,其中试卷共60页, 欢迎下载使用。
专题04 轨迹方程的求法-高考数学满分突破之解析几何篇: 这是一份专题04 轨迹方程的求法-高考数学满分突破之解析几何篇,文件包含专题04轨迹方程的求法教师版docx、专题04轨迹方程的求法学生版docx等2份试卷配套教学资源,其中试卷共57页, 欢迎下载使用。
专题03 中点弦问题(点差法)-高考数学满分突破之解析几何篇: 这是一份专题03 中点弦问题(点差法)-高考数学满分突破之解析几何篇,文件包含专题03中点弦问题点差法教师版doc、专题03中点弦问题点差法学生版docx等2份试卷配套教学资源,其中试卷共74页, 欢迎下载使用。