

2021-2022学年广东省深圳市高一(下)期末数学试卷
展开2021-2022学年广东省深圳市高一(下)期末数学试卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1.(5分)已知集合A={x|﹣3<x<2},B={0,1,2,3},则A∩B=( )
A.{0,1} B.{0,2} C.{1,2} D.{2,3}
2.(5分)设复数z=i(i+2)(其中i为虚数单位),则复数z在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.(5分)已知向量,,且,则λ=( )
A.﹣2 B. C. D.2
4.(5分)已知,,则sin(π+α)的值为( )
A. B. C. D.
5.(5分)已知直线m,n与平面α,β,γ,则能使α⊥β成立的充分条件是( )
A.α⊥γ,β⊥γ B.m∥α,m∥β
C.m∥α,m⊥β D.m⊥n,α∩β=m,n⊂β
6.(5分)下列不等式恒成立的是( )
A. B.
C. D.a2+b2≥﹣2ab
7.(5分)如图,在平行四边形ABCD中,M为AB的中点,AC与DM交于点O,则=( )
A. B. C. D.
8.(5分)已知函数,则方程f(x)﹣3|x|=0的解的个数是( )
A.0 B.1 C.2 D.3
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
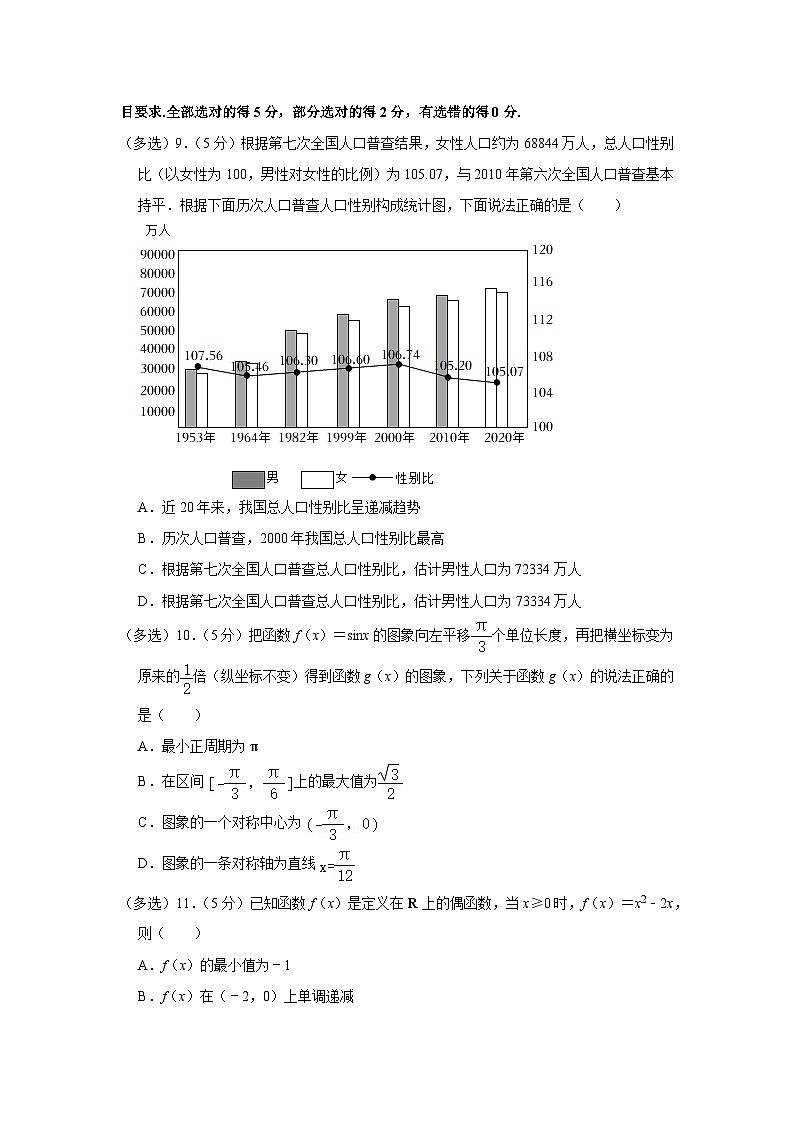
(多选)9.(5分)根据第七次全国人口普查结果,女性人口约为68844万人,总人口性别比(以女性为100,男性对女性的比例)为105.07,与2010年第六次全国人口普查基本持平.根据下面历次人口普查人口性别构成统计图,下面说法正确的是( )
A.近20年来,我国总人口性别比呈递减趋势
B.历次人口普查,2000年我国总人口性别比最高
C.根据第七次全国人口普查总人口性别比,估计男性人口为72334万人
D.根据第七次全国人口普查总人口性别比,估计男性人口为73334万人
(多选)10.(5分)把函数f(x)=sinx的图象向左平移个单位长度,再把横坐标变为原来的倍(纵坐标不变)得到函数g(x)的图象,下列关于函数g(x)的说法正确的是( )
A.最小正周期为π
B.在区间上的最大值为
C.图象的一个对称中心为
D.图象的一条对称轴为直线
(多选)11.(5分)已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x,则( )
A.f(x)的最小值为﹣1
B.f(x)在(﹣2,0)上单调递减
C.f(x)≤0的解集为[﹣2,2]
D.存在实数x满足f(x+2)+f(﹣x)=0
(多选)12.(5分)如图,在菱形ABCD中,AB=2,,将△ABD沿BD折起,使A到A',点A'不落在底面BCD内,若M为线段A'C的中点,则在△ABD翻折过程中,以下命题中正确的是( )
A.四面体A'﹣BCD的体积的最大值为1
B.存在某一位置,使得BM⊥CD
C.异面直线BM,A'D所成的角为定值
D.当二面角A'﹣BD﹣C的余弦值为时,四面体A'﹣BCD的外接球的半径为
三、填空题:本题共4小题,每小题5分,共20分.
13.(5分)计算的结果为 .
14.(5分)从2,3,4,5四个数中任取两个数,则两个数相差为2的概率是 .
15.(5分)将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积为 .
16.(5分)已知,若存在x2>x1>0,使得f(x2)=2f(x1),x1⋅f(x2)的取值范围是 .
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知函数(ω>0)的最小正周期为π.
(1)求的值;
(2)求函数f(x)的单调递减区间.
18.(12分)已知△ABC的内角A,B,C的对边分别为a,b,c,2asinC﹣3csinAcosB=0.
(1)求cosB的值;
(2)若,c=1,求b的值.
19.(12分)已知函数是定义在R上的奇函数.
(1)若,求x的值;
(2)若x∈[0,3]时,不等式f(t﹣2x)+f(x2)≤0恒成立,求实数t的取值范围.
20.(12分)BMI(身体质量指数)是目前国际上常用的衡量人体胖瘦程度以及是否健康的一个标准,其计算公式是:.在我国,成人的BMI数值参考标准为:BMI<18.5为偏瘦;18.5≤BMI<24为正常;24≤BMI<28为偏胖;28≤BMI为肥胖.某大学为了解学生的身体肥胖情况,研究人员从学校的学生体检数据中,采用比例分配的分层随机抽样的方法抽取了60名男学生,40名女学生的身高体重数据,计算出他(她)们的BMI,整理得到如图的频率分布表和频率分布直方图.同一组中的数据用该组区间的中点值作代表,用样本估计总体.
分组
频数
频率
[14,18)
15
0.15
[18,22)
40
0.40
[22,26)
30
0.30
[26,30)
10
0.10
[30,34)
5
0.05
合计
100
1.00
(1)根据BMI及频率分布直方图,估计该校学生为肥胖的百分比;
(2)已知样本中60名男学生BMI的平均数为μ1=22.8,根据频率分布直方图,估计样本中40名女学生BMI的平均数μ2.
21.(12分)如图,在四棱锥P﹣ABCD,底面ABCD为梯形,且,BC∥AD,等边三角形PCD所在的平面垂直于底面ABCD,BC⊥PD.
(1)求证:BC⊥平面PCD;
(2)若直线PB与平面ABCD所成角的正弦值为,求二面角P﹣AB﹣D的余弦值.
22.(12分)已知二次函数y=f(x)的图象经过原点,且y=f(x﹣1)是偶函数,方程f(x)+1=0有两相等实根.
(1)求y=f(x)的解析式;
(2)讨论函数与h(x)=2m2ex﹣m+2的图象的公共点个数.
2021-2022学年广东省深圳市高一(下)期末数学试卷
参考答案与试题解析
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求.
1.(5分)已知集合A={x|﹣3<x<2},B={0,1,2,3},则A∩B=( )
A.{0,1} B.{0,2} C.{1,2} D.{2,3}
【分析】利用交集定义直接求解.
【解答】解:∵集合A={x|﹣3<x<2},B={0,1,2,3},
∴A∩B={0,1}.
故选:A.
【点评】本题考查集合的运算,考查交集定义、不等式性质等基础知识,考查运算求解能力,是基础题.
2.(5分)设复数z=i(i+2)(其中i为虚数单位),则复数z在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【分析】根据复数的四则运算,先对z化简,再结合复数的几何意义,即可求解.
【解答】解:z=i(i+2)=﹣1+2i,
则复数z在复平面内对应的点(﹣1,2)位于第二象限.
故选:B.
【点评】本题主要考查复数的四则运算,以及复数的几何意义,属于基础题.
3.(5分)已知向量,,且,则λ=( )
A.﹣2 B. C. D.2
【分析】根据已知条件,结合向量垂直的性质,即可求解.
【解答】解:∵,,且,
∴1×λ﹣2×1=0,解得λ=2.
故选:D.
【点评】本题主要考查向量垂直的性质,属于基础题.
4.(5分)已知,,则sin(π+α)的值为( )
A. B. C. D.
【分析】由已知求得sinα,再由诱导公式求sin(π+α)的值.
【解答】解:∵,,∴sinα=,
∴sin(π+α)=﹣sinα=﹣.
故选:A.
【点评】本题考查三角函数的化简求值,考查诱导公式及同角三角函数基本关系式的应用,是基础题.
5.(5分)已知直线m,n与平面α,β,γ,则能使α⊥β成立的充分条件是( )
A.α⊥γ,β⊥γ B.m∥α,m∥β
C.m∥α,m⊥β D.m⊥n,α∩β=m,n⊂β
【分析】根据线面平行、垂直的判定定理和性质定理,逐项判断即可.
【解答】解:对于A,平面间的垂直关系,不具有传递性,故A错误;
对于B,如图,在长方体ABCD﹣EFGH中,EF∥平面ABCD,EF∥平面DCGH,但平面ABCD∩平面DCGH=CD,故B错误;
对于C,若m∥α,则必在α中存在直线l∥m,因为m⊥β,则l⊥β,故α⊥β,故C正确;
对于D,如图,平面ADHE∩平面BDHF=HD,AD⊥HD,HD⊂平面ADHE,但平面ADHE与平面BDHF不垂直,故D错误.
故选:C.
【点评】本题考查空间位置关系的判断,注意以长方体为载体分析解决有关问题,属于中档题.
6.(5分)下列不等式恒成立的是( )
A. B.
C. D.a2+b2≥﹣2ab
【分析】利用a,b异号可判断A,B不成立,a,b均小于0可判断C,利用(a+b)2≥0可判断D.
【解答】解:对于A:a,b异号是显然不成立,∴A不正确;
对于B:a,b异号是显然不成立,∴B不正确;
对于C:a,b均小于0时,显然不成立,∴C不正确;
对于D:∵(a+b)2≥0 (a,b∈R),∴a2+b2≥﹣2ab (a,b∈R),∴D正确;
故选:D.
【点评】本题主要考查了基本不等式的成立条件的检验,属于基础题.
7.(5分)如图,在平行四边形ABCD中,M为AB的中点,AC与DM交于点O,则=( )
A. B. C. D.
【分析】首先由三角形AOM与三角形DOC相似可得DO=2OM,从而可得,再利用三角形法则转化即可.
【解答】解:因为ABCD为平行四边形,故AB∥CD,故易知△AOM∽△COD,
故可得,
故=,
故选:A.
【点评】本题主要考查平面向量基本定理的应用,属于基础题.
8.(5分)已知函数,则方程f(x)﹣3|x|=0的解的个数是( )
A.0 B.1 C.2 D.3
【分析】令y=3|x|,则方程f(x)﹣3|x|=0的解的个数即函数y=f(x)与函数y=3|x|的图象的交点的个数.作出函数与函数的图象,即可得到两个函数图象的交点的个数.
【解答】解:令f(x)﹣3|x|=0,得f(x)=3|x|,
则方程f(x)﹣3|x|=0的解的个数即函数y=f(x)与函数y=3|x|的图象的交点的个数.
作出函数y=f(x)与函数y=3|x|的图象,可知两个函数图象的交点的个数为2,
故方程的解的个数为2个.
故选:C.
【点评】本题考查了方程的解的个数,也考查了转化思想、数形结合思想,作出图象是解答本题的关键,属于基础题.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
(多选)9.(5分)根据第七次全国人口普查结果,女性人口约为68844万人,总人口性别比(以女性为100,男性对女性的比例)为105.07,与2010年第六次全国人口普查基本持平.根据下面历次人口普查人口性别构成统计图,下面说法正确的是( )
A.近20年来,我国总人口性别比呈递减趋势
B.历次人口普查,2000年我国总人口性别比最高
C.根据第七次全国人口普查总人口性别比,估计男性人口为72334万人
D.根据第七次全国人口普查总人口性别比,估计男性人口为73334万人
【分析】根据统计图提供的数据判断.
【解答】解:近20年来,我国总人口性别比呈递减趋势,所以A正确;
由统计图数据知,历次人口普查,1953年我国总人口性别比最高,所以B不正确;
根据第七次全国人口普查总人口性别比,设男性人口为x,,x≈72334,则估计男性人口为72334万人,故C正确,D不正确.
故选:AC.
【点评】本题考查由频率分布直方图求频数,属于基础题.
(多选)10.(5分)把函数f(x)=sinx的图象向左平移个单位长度,再把横坐标变为原来的倍(纵坐标不变)得到函数g(x)的图象,下列关于函数g(x)的说法正确的是( )
A.最小正周期为π
B.在区间上的最大值为
C.图象的一个对称中心为
D.图象的一条对称轴为直线
【分析】首先利用平移变换和伸缩变换的应用求出函数g(x)的关系式,进一步利用函数的性质求出结果.
【解答】解:f(x)=sinx的图象向左平移个单位长度,再把横坐标变为原来的倍(纵坐标不变)得到函数g(x)=sin(2x+)的图象;
所以函数的最小正周期为π,
当x=时,函数取得最大值1.
故选:AD.
【点评】本题考查的知识要点:三角函数关系式的平移变换和伸缩变换,函数的性质的应用,主要考查学生的运算能力和数学思维能力,属于基础题.
(多选)11.(5分)已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x,则( )
A.f(x)的最小值为﹣1
B.f(x)在(﹣2,0)上单调递减
C.f(x)≤0的解集为[﹣2,2]
D.存在实数x满足f(x+2)+f(﹣x)=0
【分析】由偶函数的定义可得f(x)的解析式,由二次函数的最值求法和单调性的判断、二次不等式的解法和f(0)=f(2)=f(﹣2)=0,可得结论.
【解答】解:函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x=(x﹣1)2﹣1,
可得f(x)=,
可得x≥0时,f(x)在x=1时取得最小值﹣1,由偶函数的图象关于y轴对称,可得f(x)在 R上取得最小值﹣1,故A正确;
f(x)在(﹣∞,﹣1)递减,在(﹣1,0)递增,故 B错误;
由或,
解得:0≤x≤2,或﹣2≤x<0,故C正确;
由f(0)=0,f(﹣2)=f(2)=0,即存在实数x满足f(x+2)+f(﹣x)=0,故D正确.
故选:ACD.
【点评】本题考查函数的奇偶性和单调性的性质和运用,考查转化思想、运算能力,属于中档题
(多选)12.(5分)如图,在菱形ABCD中,AB=2,,将△ABD沿BD折起,使A到A',点A'不落在底面BCD内,若M为线段A'C的中点,则在△ABD翻折过程中,以下命题中正确的是( )
A.四面体A'﹣BCD的体积的最大值为1
B.存在某一位置,使得BM⊥CD
C.异面直线BM,A'D所成的角为定值
D.当二面角A'﹣BD﹣C的余弦值为时,四面体A'﹣BCD的外接球的半径为
【分析】连接AC交BD于O,连接OA′,取CD的中点N,连接MN,BN,当平面A′BD⊥平面BCD时,四面体A'﹣BCD的体积最大,从而可判断A;
易得BN⊥CD,说明成立MN⊥CD,再根据线面垂直的判定定理及性质即可判断B;
证明异面直线BM,A′D,所成的角即为∠BMN或其补角,再根据BM不为定值,即可判断C;
说明∠A′OC即为二面角的平面角,再根据二面角的余弦值可得A′C=2,补全为正方体,从而可判断D.
【解答】解:连接AC交BD于O,连接OA′,取CD的中点N,连接MN,BN,
对于A,当平面A′BD⊥平面BCD时,四面体A'﹣BCD的体积最大,
点A′到平面BCD的距离最大,此时在菱形ABCD中AB=2,∠BAD=,
则△ABD,△BCD都是等边三角形,
则OA′=OA=OC=,
此时四面体A'﹣BCD的体积为=1,
所以四面体A'﹣BCD的体积的最大值为1,故A正确;
对于B,因为M,N分别为′C,CD的中点,
所以BN⊥CD,MN∥A′D且MN=A′D=1,
由题意∠A′DC∈(0,),则∠MNC∈(0,),
当∠MNC=时,MN⊥CD,
因为MN∩BN=N,
所以当∠MNC=时,CD⊥平面BMN,
又BM⊂平面BMN,
所以CD⊥BM,
所以存在某一位置,使得BM⊥CD,故B正确;
对于C,因为MN∥A′D,
所以异面直线BM,A′D所成的角即为∠BMN或其补角,
cos∠BMN==﹣,
因为BM不为定值,所以cos∠BMN不为定值,
即异面直线BM,A′D,所成的角不为定值,故C错误;
对于D,因为OC⊥BD,OA′⊥BD,
所以∠A′OC即为二面角A'﹣BD﹣C的平面角,
则∠A′OC===,所以A′C=2,
所以四面体A'﹣BCD为正四面体,
如图,补全正四面体A'﹣BCD为正方体,
则正方体的棱长为,
则这个正方体外接球的半径为=,
即四面体的A'﹣BCD外接球的半径为,故D正确.
故选:ABD.
【点评】本题考查了直线与直线所成角、二面角、棱锥的体积公式及用补形法求几何体外接圆的半径,属于中档题.
三、填空题:本题共4小题,每小题5分,共20分.
13.(5分)计算的结果为 2 .
【分析】根据指数与对数的运算性质化简即可求解.
【解答】解:(+ln=[(3]+ln
==2,
故答案为:2.
【点评】本题考查了指数与对数的运算性质,考查了学生的运算能力,属于基础题.
14.(5分)从2,3,4,5四个数中任取两个数,则两个数相差为2的概率是 .
【分析】由题意可得:从2,3,4,5这四个数中任取两个共有6个基本事件,而符合条件的共有2个,由古典概型的公式可得答案.
【解答】解:由题意可得:从2,3,4,5四个数中任取两个数,共有6个基本事件,
即(2,3),(2,4),(2,5),(3,4),(3,5),(4,5);
而符合条件的共有(2,4),(3,5)共2个,
故所求概率为:=.
故答案为:.
【点评】本题主要考查古典概型的问题,熟记概率的计算公式即可,属于常考题型.
15.(5分)将边长为1的正方形以其一边所在直线为旋转轴旋转一周,所得几何体的侧面积为 2π .
【分析】边长为1的正方形,绕其一边所在直线旋转一周,得到的几何体为圆柱,从而可求圆柱的侧面积.
【解答】解:边长为1的正方形,绕其一边所在直线旋转一周,得到的几何体为圆柱,
则所得几何体的侧面积为:1×2π×1=2π,
故答案为:2π
【点评】本题是基础题,考查旋转体的侧面积的求法,考查计算能力.
16.(5分)已知,若存在x2>x1>0,使得f(x2)=2f(x1),x1⋅f(x2)的取值范围是 (0,)∪[4,+∞) .
【分析】分0<x1<x2<1,0<x1<1≤x2,1≤x1<x2三种情况讨论,由题意x1⋅f(x2)=2x1⋅f(x1),分别确定x1的范围,再结合函数的单调性即可得出答案.
【解答】解:当0<x1<x2<1时,
则f(x2)=2f(x1)∈(0,1),
所以f(x1)∈(0,),即x12∈(0,),
所以x1∈(0,),
则x1⋅f(x2)=2x1⋅f(x1)=2x13,
因为函数y=x3在(0,1)上递增,
所以x1⋅f(x2)=2x13∈(0,);
当0<x1<1≤x2,
f(x1)=x12∈(0,1),
所以f(x2)=∈[2,+∞),
所以f(x2)>2f(x1),不存在0<x1<1≤x2,使得f(x2)=2f(x1);
当1≤x1<x2时,
则f(x1)=,f(x2)=,
因为f(x2)=2f(x1),
所以=×2,
所以x2=x1+1,
则x1⋅f(x2)=2x1⋅f(x1)=2x1•,
令g(x)=2x•2x,x∈[1,+∞),
则==•,
因为1≤x1<x2,
所以<1,x1﹣x2<0,
所以<1,所以•<1,
即g(x1)<g(x2),
所以函数g(x)=2x•2x在[1,+∞)上递增,
所以g(x)≥g(1)=4,即x1⋅f(x2)∈[4,+∞),
综上所述,x1⋅f(x2)的取值范围是(0,)∪[4,+∞).
故答案为:(0,)∪[4,+∞).
【点评】本题考查了求函数的值域,也考查了转化思想、分类讨论思想,属于中档题.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(10分)已知函数(ω>0)的最小正周期为π.
(1)求的值;
(2)求函数f(x)的单调递减区间.
【分析】(1)由题意利用正弦函数的周期公式可求ω,可得函数解析式为f(x)=2sin(2x+),即可计算求解.
(2)利用正弦函数的单调性即可求解.
【解答】解:(1)因为函数(ω>0)的最小正周期为π,
所以π=,可得ω=2,可得f(x)=2sin(2x+),
所以=2sin(2×+)=;
(2)由(1)可得f(x)=2sin(2x+),
令2kπ+≤2x+≤2kπ+,k∈Z,解得kπ+≤x≤kπ+,k∈Z,
可得函数f(x)的单调递减区间为:[kπ+,kπ+],k∈Z.
【点评】本题考查了正弦函数的周期公式以及正弦函数的单调性,考查了函数思想,属于基础题.
18.(12分)已知△ABC的内角A,B,C的对边分别为a,b,c,2asinC﹣3csinAcosB=0.
(1)求cosB的值;
(2)若,c=1,求b的值.
【分析】(1)利用正弦定理将角化边,即可求出cosB;
(2)根据数量积的定义求出ac,即可求出a,再由余弦定理计算可得.
【解答】(1)解:因为2asinC﹣3csinAcosB=0,
由正弦定理可得2ac﹣3accosB=0,因为ac≠0,所以;
(2)解:因为,所以accosB=2,所以ac=3,
因为c=1,所以a=3,
由余弦定理,
所以.
【点评】本题考查了正余弦定理在解三角形中的应用,属于基础题.
19.(12分)已知函数是定义在R上的奇函数.
(1)若,求x的值;
(2)若x∈[0,3]时,不等式f(t﹣2x)+f(x2)≤0恒成立,求实数t的取值范围.
【分析】(1)根据奇函数的性质得到f(0)=0,即可求出a,从而得到f(x)的解析式,再解方程即可;
(2)首先判断函数的单调性,结合奇偶性与单调性得到t﹣2x≤﹣x2在x∈[0,3]上恒成立,参变分离可得t≤﹣x2+2x,x∈[0,3]恒成立,根据二次函数的性质求出﹣x2+2x的最小值,即可得解.
【解答】解:(1)因为函数是定义在R上的奇函数,所以f(0)=0,
即,解得a=1,
所以,即f(x)=2x﹣2﹣x,则f(﹣x)=2﹣x﹣2x=﹣f(x),符合题意,
又,即,
即2⋅4x﹣3⋅2x﹣2=0,即(2⋅2x+1)(2x﹣2)=0,
即2x﹣2=0,解得x=1;
解:因为,
所以f(x)在定义域上单调递增,又f(x)是定义在R上的奇函数,
所以f(t﹣2x)+f(x2)≤0在x∈[0,3]恒成立,
等价于f(t﹣2x)≤﹣f(x2)=f(﹣x2)在x∈[0,3]上恒成立,
即t﹣2x≤﹣x2在x∈[0,3]上恒成立,即t≤﹣x2+2x,x∈[0,3]恒成立,
令g(x)=﹣x2+2x=﹣(x﹣1)2+1,x∈[0,3],
所以g(x)在[0,1]上单调递增,在(1,3]上单调递减,g(0)=0,g(3)=﹣3,
所以g(x)min=﹣3,所以t≤﹣3,
即t∈(﹣∞,﹣3];
【点评】本题考查了函数的奇偶性的应用以及不等式的恒成立问题,属于中档题.
20.(12分)BMI(身体质量指数)是目前国际上常用的衡量人体胖瘦程度以及是否健康的一个标准,其计算公式是:.在我国,成人的BMI数值参考标准为:BMI<18.5为偏瘦;18.5≤BMI<24为正常;24≤BMI<28为偏胖;28≤BMI为肥胖.某大学为了解学生的身体肥胖情况,研究人员从学校的学生体检数据中,采用比例分配的分层随机抽样的方法抽取了60名男学生,40名女学生的身高体重数据,计算出他(她)们的BMI,整理得到如图的频率分布表和频率分布直方图.同一组中的数据用该组区间的中点值作代表,用样本估计总体.
分组
频数
频率
[14,18)
15
0.15
[18,22)
40
0.40
[22,26)
30
0.30
[26,30)
10
0.10
[30,34)
5
0.05
合计
100
1.00
(1)根据BMI及频率分布直方图,估计该校学生为肥胖的百分比;
(2)已知样本中60名男学生BMI的平均数为μ1=22.8,根据频率分布直方图,估计样本中40名女学生BMI的平均数μ2.
【分析】(1)由频率分布直方图求得28≤BMI≤30的频率,从而可得该校学生为肥胖的百分比;
(2)先根据频率分布直方图求出样本的BMI的平均数,再根据样本的BMI的平均数等于,即可得解.
【解答】解:(1)由频率分布直方图可知28≤BMI≤30的频率为=0.05,
所以28≤BMI的频率为:0.05+0.05=0.1,
所以估计该校学生为肥胖的百分比为10%;
(2)样本的BMI的平均数为16×0.15+20×0.4+24×0.3+28×0.1+32×0.05=22,
则=22,
解得:μ2=20.8,
所以估计样本中40名女学生BMI的平均数20.8.
【点评】本题考查由频率分布表、直方图求频率、平均数,属于基础题.
21.(12分)如图,在四棱锥P﹣ABCD,底面ABCD为梯形,且,BC∥AD,等边三角形PCD所在的平面垂直于底面ABCD,BC⊥PD.
(1)求证:BC⊥平面PCD;
(2)若直线PB与平面ABCD所成角的正弦值为,求二面角P﹣AB﹣D的余弦值.
【分析】(1)利用面面垂直证明线面垂直,进而可得异面直线垂直,可证线面垂直;
(2)分别过点D与点P作直线AB的垂线,再通过平行,构造二面角的平面角,进而可得二面角余弦值.
【解答】证明:(1)如图所示,取CD中点O,连接PO,
∵△PCD是正三角形,∴PO⊥CD
又平面PCD⊥平面ABCD,且平面PCD∩平面ABCD=CD,
∴PO⊥平面ABCD,BC⊂平面ABCD,∴PO⊥BC,
∵BC⊥PD,且PO∩PD=P,
∴BC⊥平面PCD;
如图所示,连接OB,BD,过点D,P作DM⊥AB,PN⊥AB,分别与AB交于点M,N,过点M作MQ∥NP,交AP于点Q
,连接DQ,
设AD=2BC=2,CD=2a,a>0,则,
由(1)得OP⊥平面ABCD,∴∠OBP即为直线PB与平面ABCD所成角的平面角,
BC⊥平面PCD,∴BC⊥CP,
则,
解得:a=1,
故,且,
即,解得
又BC∥AD,所以AD⊥平面PCD,AD⊥PD,
,且,
即,解得,
所以点M为线段AN的中点,故点Q也为线段AP中点,
所以,
所以∠DMQ即为二面角P﹣AB﹣D的平面角,
.
【点评】本题考查二面角,考查学生的运算能力,属于中档题.
22.(12分)已知二次函数y=f(x)的图象经过原点,且y=f(x﹣1)是偶函数,方程f(x)+1=0有两相等实根.
(1)求y=f(x)的解析式;
(2)讨论函数与h(x)=2m2ex﹣m+2的图象的公共点个数.
【分析】(1)设f(x)=ax2+bx+c(a≠0),易得c=0,根据y=f(x﹣1)是偶函数,可得a,b的一个关系式,再根据方程ax2+2ax+1=0有两相等实根,可得根的判别式Δ=0,从而可求得a,b,即可得解;
(2)函数g(x)与h(x)的图象的公共点个数,即方程=2m2ex﹣m+2的实数根的个数,即方程(2m2﹣1)(ex)2﹣mex﹣1=0的实数根的个数,令t=ex,t∈(0,+∞),故所求转化为方程(2m2﹣1)t2﹣mt﹣1=0在t∈(0,+∞)在实根的个数,再分2m2﹣1=0,2m2﹣1>0,2m2﹣1<0三种情况讨论,从而可得出结论.
【解答】解:(1)设f(x)=ax2+bx+c(a≠0),
因为二次函数y=f(x)的图象经过原点,
所以c=0,
y=f(x﹣1)=a(x﹣1)2+b(x﹣1)=ax2+(b﹣2a)x+a﹣b,
因为y=f(x﹣1)是偶函数,
所以b﹣2a=0,
即b=2a,
所以f(x)=ax2+2ax(a≠0),
又方程ax2+2ax+1=0有两个相等的实数根,
所以Δ=4a2﹣4a=0,
解得a=1(a=0舍去),
所以f(x)=x2+2x;
(2)由(1)得=,
令g(x)=h(x),
则=2m2ex﹣m+2,
即(ex)2+2ex+1=2m2(ex)2﹣mex+2ex,
即(2m2﹣1)(ex)2﹣mex﹣1=0,
令t=ex,t∈(0,+∞),
则(2m2﹣1)t2﹣mt﹣1=0,
故所求转化为方程(2m2﹣1)t2﹣mt﹣1=0在t∈(0,+∞)实根的个数,
令φ(t)=(2m2﹣1)t2﹣mt﹣1,t∈(0,+∞),
①当2m2﹣1=0,即m=时,
若m=,则﹣t﹣1=0,故t=﹣<0,
所以m=时,方程无实根;
若m=﹣,则t﹣1=0,故t=,
所以m=﹣时,方程有1个实根;
②当2m2﹣1>0,即m<﹣或m>时,
因为Δ=m2+8m2﹣4=9m2﹣4>0,且φ(0)=﹣1,两根之积<0,
所以当m<﹣或m>时,方程有1正个实根;
③当2m2﹣1<0,即﹣<m<时,>0,即如果有两根,则两根同号
若,即﹣<m<﹣时,方程有两正实数根,
若,即<m<时,方程有两个不相等的负实根,不符题意;
若,即m=﹣时,方程有1个实根,
若,即m=时,方程无正实根,
若,即﹣<m<时,方程无实根,
综上所述,m=时,方程无实根;
当m∈(﹣∞,﹣]∪{﹣}∪(,+∞)时,函数的g(x),h(x)图象有1个公共点;
当m∈(﹣,﹣)时,函数g(x),h(x)的图象有2个公共点
当(﹣,)时,函数g(x),h(x)的图象没有公共点;
当m∈(,)时,函数g(x),h(x)的图象没有公共点.
【点评】本题考查了根据待定系数法球二次函数的解析式,考查了偶函数的性质及一元二次方程的根的问题,考查了一元二次方程在某个区间上的实根的个数问题,考查了分类讨论思想,对数据分析的能力要求较高,属于难题.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2023/5/27 16:18:32;用户:数学;邮箱:13172290467;学号:37324361
2022-2023学年广东省深圳市高一(上)期末数学试卷: 这是一份2022-2023学年广东省深圳市高一(上)期末数学试卷,共16页。试卷主要包含了选择题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年广东省深圳市龙华区高一(上)期末数学试卷: 这是一份2022-2023学年广东省深圳市龙华区高一(上)期末数学试卷,共14页。试卷主要包含了单项选择题,多项选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年广东省深圳市高一(下)期末数学试卷(含解析): 这是一份2022-2023学年广东省深圳市高一(下)期末数学试卷(含解析),共18页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












