浙江温州市2023年各地区中考数学模拟（一模）试题按题型难易度分层分类汇编（7套）-02填空题（提升题）

这是一份浙江温州市2023年各地区中考数学模拟（一模）试题按题型难易度分层分类汇编（7套）-02填空题（提升题），共18页。

浙江温州市2023年各地区中考数学模拟（一模）试题按题型难易度分层分类汇编（7套）-02填空题（提升题）
一．解一元一次不等式组（共1小题）
1．（2023•龙湾区一模）不等式组的解为 　 　．
二．反比例函数系数k的几何意义（共1小题）
2．（2023•平阳县一模）如图，点A，B，C在函数（常数k＞0，x＞0）图象上的位置如图所示，分别过点A，C作x轴与y轴的垂线，过点B作y轴与CD的垂线．若OD：DE：EF＝2：1：3，图中所构成的阴影部分面积为2，则矩形IGHC的面积为 　 　．

三．勾股定理（共1小题）
3．（2023•龙湾区一模）图1是某收纳盒实物图，图2是盒子打开时部分侧面示意图，两平行的支撑杆AC，BE与收纳盒相连．当支撑杆绕点A或B旋转时，收纳盒CD，EF沿斜上方平移，且CD，EF始终保持与MN平行．点A位于PQ的中垂线上，其到PQ的距离是到MN距离的1.5倍，已知PQ＝31cm，AB∥PQ，AB＝8.5cm．转动BE，当点E在点B的正上方时，E到MN的距离为18cm，盒子关闭时，支撑杆BE绕点B旋转，点E恰好与点M重合，则支撑杆BE的长为 　 　cm；将盒子完全打开如图3所示，支撑杆BE经过点N，则EF与PQ的距离为 　 　cm．

四．菱形的性质（共1小题）
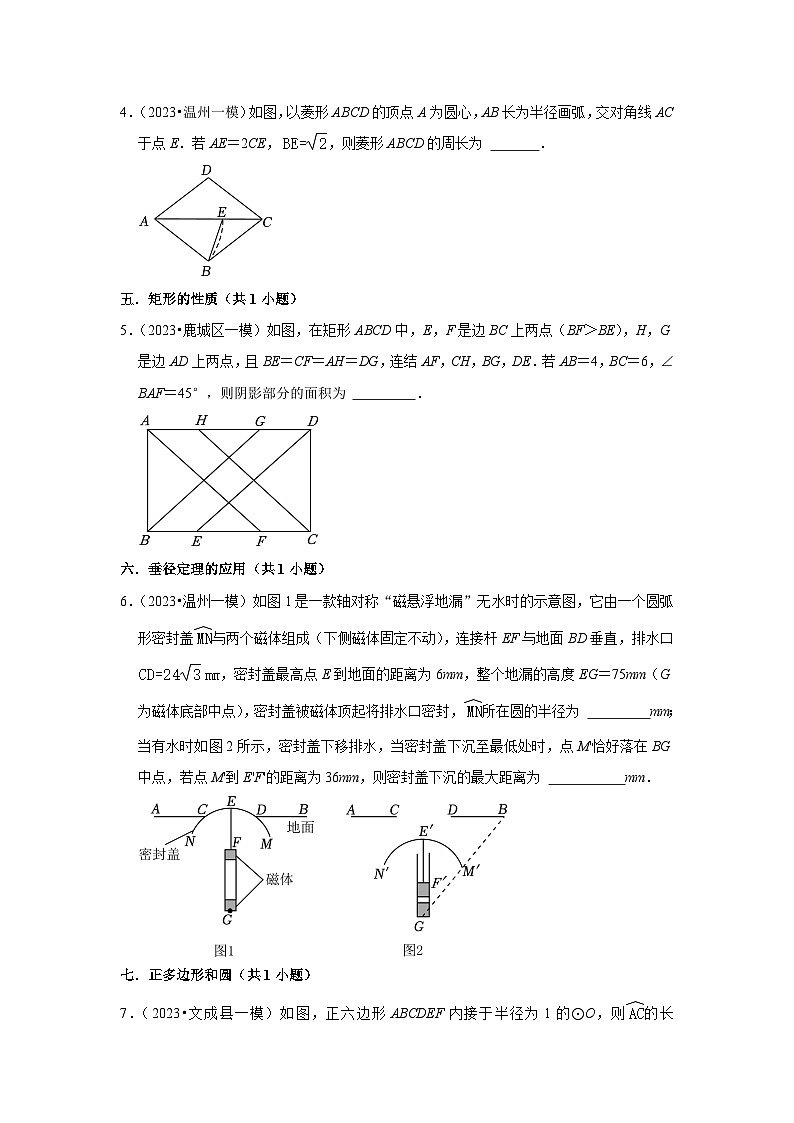
4．（2023•温州一模）如图，以菱形ABCD的顶点A为圆心，AB长为半径画弧，交对角线AC于点E．若AE＝2CE，，则菱形ABCD的周长为 　 　．

五．矩形的性质（共1小题）
5．（2023•鹿城区一模）如图，在矩形ABCD中，E，F是边BC上两点（BF＞BE），H，G是边AD上两点，且BE＝CF＝AH＝DG，连结AF，CH，BG，DE．若AB＝4，BC＝6，∠BAF＝45°，则阴影部分的面积为 　 　．

六．垂径定理的应用（共1小题）
6．（2023•温州一模）如图1是一款轴对称“磁悬浮地漏”无水时的示意图，它由一个圆弧形密封盖与两个磁体组成（下侧磁体固定不动），连接杆EF与地面BD垂直，排水口，密封盖最高点E到地面的距离为6mm，整个地漏的高度EG＝75mm（G为磁体底部中点），密封盖被磁体顶起将排水口密封，所在圆的半径为 　 　mm；当有水时如图2所示，密封盖下移排水，当密封盖下沉至最低处时，点M'恰好落在BG中点，若点M'到E'F'的距离为36mm，则密封盖下沉的最大距离为 　 　mm．

七．正多边形和圆（共1小题）
7．（2023•文成县一模）如图，正六边形ABCDEF内接于半径为1的⊙O，则的长为​　 　．

八．弧长的计算（共2小题）
8．（2023•平阳县一模）一个扇形的半径为6，弧长为3π，则此扇形的圆心角为　 　度．
9．（2023•文成县一模）图1是小文家的木马玩具，图2是木马玩具底座水平放置的示意图，点O是所在圆的圆心，OA＝OB，点A，点B离地高度均为15cm，水平距离AB＝90cm，则OA＝　 　cm，当半径OA转到竖直位置时，木马就有翻倒的风险，为安全起见，点B离地高度应小于 　 　cm．

九．相似三角形的应用（共2小题）
10．（2023•平阳县一模）图1是一种机械装置，当滑轮P绕固定点O旋转时，点P在AB上滑动，带动点B绕固定点A旋转，使点C在水平杆MN上来回滑动．图2是装置的侧面示意图，AO⊥MN，OA＝10cm，AB＝18cm，BC＝12cm，OP＝6cm．当转动到OP′⊥AB′时，点C滑到最左边C′处，此时A，B′，C′恰好在同一条直线上，则点O到MN的距离是 　 　cm；当转动到OP′′⊥AB′′时，点C滑到最右边C′′处，则点C在MN上滑动的最大距离C′C′′＝　 　cm．

11．（2023•瓯海区一模）甲、乙两幢完全一样的房子如图1，小聪与弟弟住在甲幢，为测量对面的乙幢屋顶斜坡M，N之间的距离，制定如下方案：两幢房子截面图如图2，AB＝12m，小聪在离屋檐A处3m的点G处水平放置平面镜（平面镜的大小忽略不计），弟弟在离点G水平距离3m的点H处恰好在镜子中看到乙幢屋顶N，此时测得弟弟眼睛与镜面的竖直距离IH＝0.6m．下楼后，弟弟直立站在DE处，测得地面点F与E，M，N在一条直线上，DE＝1.2m，FD＝2m，BF＝5m，则甲、乙两幢间距BC＝　 　m，乙幢屋顶斜坡M，N之间的距离为 　 　m．



浙江温州市2023年各地区中考数学模拟（一模）试题按题型难易度分层分类汇编（7套）-02填空题（提升题）
参考答案与试题解析
一．解一元一次不等式组（共1小题）
1．（2023•龙湾区一模）不等式组的解为 　﹣3＜x≤2　．
【答案】﹣3＜x≤2．
【解答】解：，
解不等式①，得x＞﹣3；
解不等式②，得x≤2；
故不等式组的解集为﹣3＜x≤2．
故答案为：﹣3＜x≤2．
二．反比例函数系数k的几何意义（共1小题）
2．（2023•平阳县一模）如图，点A，B，C在函数（常数k＞0，x＞0）图象上的位置如图所示，分别过点A，C作x轴与y轴的垂线，过点B作y轴与CD的垂线．若OD：DE：EF＝2：1：3，图中所构成的阴影部分面积为2，则矩形IGHC的面积为 　8　．

【答案】8．
【解答】解：由于OD：DE：EF＝2：1：3，可设OD＝2a，则DE＝a，EF＝3a，设OG＝b，
∵点A、B、C都在反比例函数y＝的图象上，
∴S矩形AFOG＝S矩形ODCH，
即6ab＝2a×OH，
∴OH＝3b，
∴GH＝OH﹣OG＝2b，
又∵OE•BE＝k＝OG•OF，
即3a•BE＝6ab，
∴BE＝2b，
∴阴影矩形的两条边的长分别为a、b，
又∵阴影矩形的面积为2，
∴ab＝2，
∴矩形IGHC的面积为OD•GH＝2a•2b＝4ab＝8．
故答案为：8．
三．勾股定理（共1小题）
3．（2023•龙湾区一模）图1是某收纳盒实物图，图2是盒子打开时部分侧面示意图，两平行的支撑杆AC，BE与收纳盒相连．当支撑杆绕点A或B旋转时，收纳盒CD，EF沿斜上方平移，且CD，EF始终保持与MN平行．点A位于PQ的中垂线上，其到PQ的距离是到MN距离的1.5倍，已知PQ＝31cm，AB∥PQ，AB＝8.5cm．转动BE，当点E在点B的正上方时，E到MN的距离为18cm，盒子关闭时，支撑杆BE绕点B旋转，点E恰好与点M重合，则支撑杆BE的长为 　25　cm；将盒子完全打开如图3所示，支撑杆BE经过点N，则EF与PQ的距离为 　　cm．

【答案】25；．
【解答】解：如图2：设BE与MN相交于点O，AC与MN相交于点K，连接BN，

由题意得：MN∥PQ，MN＝PQ＝31cm，BE⊥MN，AC⊥MN，OE＝18cm，AB＝KO＝CG＝8.5cm，
设BO＝xcm，
∴BM＝BE＝BO+OE＝（x+18）cm，
∵点A位于PQ的中垂线上，
∴AC平分MN，
∴MK＝KN＝MN＝15.5（cm），
∴MN＝MK+KO＝24（cm），
在Rt△MOB中，MO2+OB2＝MB2，
∴242+x2＝（x+18）2，
∴x＝7，
∴BO＝7cm，BM＝BE＝x+18＝25（cm），
∴ON＝MN﹣MO＝31﹣24＝7（cm），
∴OB＝ON，
∴∠OBN＝∠ONB＝45°，
∴BN＝ON＝7（cm）；
如图3：过点EJ⊥QP，交QP的延长线于点J，延长AB交EJ于点I，交NP于点H，

由题意得：AH⊥NP，AI⊥EJ，PH＝IJ，
∴∠BHN＝∠BIE＝90°，
∵∠MNB＝45°，AB∥MN，
∴∠NBH＝∠MNB＝45°，
∵BN＝7cm，
∴NH＝＝7（cm），
∵BE＝25cm，
∴EI＝＝（cm），
由题意得：＝1.5，
∴PH＝1.5NH＝10.5（cm），
∴IJ＝PH＝10.5（cm），
∴EJ＝EI+IJ＝+10.5＝（cm），
∴EF与PQ的距离为cm，
故答案为：25；．
四．菱形的性质（共1小题）
4．（2023•温州一模）如图，以菱形ABCD的顶点A为圆心，AB长为半径画弧，交对角线AC于点E．若AE＝2CE，，则菱形ABCD的周长为 　8　．

【答案】8．
【解答】解：连BD交AC于点O，

∵菱形ABCD，
∴，∠BOC＝90°，
设CE＝x，则AE＝2CE＝2x，
∴AC＝3x，
∴，，
∵以A为圆心，AB长为半径画弧，交对角线AC于点E，
∴AB＝AE＝2x，
∵，
∴在Rt△BOE中，，
∵在Rt△BOA中，，
∴，
解得：x＝±1，
∵x＞0，
∴x＝1，
∴AB＝2x＝2，
∴菱形ABCD的周长为4AB＝2×4＝8，
故答案为：8．
五．矩形的性质（共1小题）
5．（2023•鹿城区一模）如图，在矩形ABCD中，E，F是边BC上两点（BF＞BE），H，G是边AD上两点，且BE＝CF＝AH＝DG，连结AF，CH，BG，DE．若AB＝4，BC＝6，∠BAF＝45°，则阴影部分的面积为 　14　．

【答案】14．
【解答】解：如图，设AF交BG，ED于点Q，T，CH交BG，ED于点P，R，

在矩形ABCD中，AD∥BC，∠ABC＝90°，
∵BE＝CF＝AH＝DG，
∴四边形AHCF，四边形DGBE是平行四边形，
∵∠BAF＝45°，
∴∠BFA＝45°，
∴△ABF是等腰直角三角形，
∴AB＝FB＝4，
∵BC＝6，
∴FC＝BC﹣BF＝2，
∴BE＝CF＝AH＝DG＝2，
∴GH＝EF＝2，
∴EC＝DC＝4，
∴△DEC是等腰直角三角形，
∴∠DEC＝45°，
∴∠ETF＝90°，
∴△TEF是等腰直角三角形，
同理△ABQ是等腰直角三角形，△BPC是等腰直角三角形，
∴BP＝CP，ET＝FT，
∴QT＝RT，
∴四边形PQTR是正方形，
∵平行四边形AHCF的面积＝CF•AB＝2×4＝8，
∴平行四边形AHCF面积＝平行四边形DGBE的面积＝8，
∵AQ＝AB＝2，FT＝EF＝，AF＝AB＝4，
∴QT＝AF﹣AQ﹣FT＝，
∴正方形PQTR的面积＝（）2＝2，
∴阴影部分的面积＝2×平行四边形AHCF的面积﹣正方形PQTR的面积＝16﹣2＝14．
故答案为：14．
六．垂径定理的应用（共1小题）
6．（2023•温州一模）如图1是一款轴对称“磁悬浮地漏”无水时的示意图，它由一个圆弧形密封盖与两个磁体组成（下侧磁体固定不动），连接杆EF与地面BD垂直，排水口，密封盖最高点E到地面的距离为6mm，整个地漏的高度EG＝75mm（G为磁体底部中点），密封盖被磁体顶起将排水口密封，所在圆的半径为 　39　mm；当有水时如图2所示，密封盖下移排水，当密封盖下沉至最低处时，点M'恰好落在BG中点，若点M'到E'F'的距离为36mm，则密封盖下沉的最大距离为 　16.5　mm．

【答案】39，16.5．
【解答】解：①设作圆心O，连接CD交CE于点H，
设OH＝xmm，
∵最高点E到地面的距离为6mm，
∴OE＝（6+x）mm，
∵，
∴，
∴在Rt△OHD中，，
∵OE＝OD，
∴，
∴x＝33，
∴OE＝39mm，
故答案为：39．

②作M'P'⊥E'G，延长GE'，交AB于点Q'，作M'Z⊥AB交AB于点Z，
∵M'P'⊥E'G，
∴M′Z∥E′G，
∴点Z是BQ'的中点，
∵M'为BG的中点，
∴M'Z为△GQ'B的中位线，
∴，
∵EG＝75mm，EQ'＝6mm，
∴GQ'＝69mm，
∴，
∵点M'到E'F'的距离为36mm，
∴MJ＝M'P'＝36mm，
∵OM＝OE＝39mm，
回到图1，作MJ⊥EG，
由勾股定理得：（mm），
∴移动前M到地面的距离为：JH＝39﹣15﹣6＝18（mm），
∵M移动的距离为密盖下沉的距离，
∴MM'＝M'Z﹣JH＝34.5﹣18＝16.5（mm），
∴密封盖下沉的最大距离为16.5mm．
故答案为：16.5．

七．正多边形和圆（共1小题）
7．（2023•文成县一模）如图，正六边形ABCDEF内接于半径为1的⊙O，则的长为​　π　．

【答案】π．
【解答】解：连接OA，OB，OC．
∵六边形ABCDEF为正六边形，
∴∠AOB＝∠BOC＝360°×＝60°，
∴∠AOC＝120°，
∴的长为＝π；
故答案为：π．

八．弧长的计算（共2小题）
8．（2023•平阳县一模）一个扇形的半径为6，弧长为3π，则此扇形的圆心角为　90　度．
【答案】见试题解答内容
【解答】解：设这个扇形的圆心角为n°，
则＝3π，
解得，n＝90，
故答案为：90．
9．（2023•文成县一模）图1是小文家的木马玩具，图2是木马玩具底座水平放置的示意图，点O是所在圆的圆心，OA＝OB，点A，点B离地高度均为15cm，水平距离AB＝90cm，则OA＝　75　cm，当半径OA转到竖直位置时，木马就有翻倒的风险，为安全起见，点B离地高度应小于 　54　cm．

【答案】75，54．
【解答】解：如图①，作半径OD⊥AB交AB于E，设OA＝xcm，
∴AE＝BE＝AB＝×90＝45cm，ED＝15cm，
设OA＝xcm，
∵OA2＝AE2+OE2，
∴x2＝452+（x﹣15）2，
∴x＝75，
∴OA＝75cm．

如图②半径OA与地面垂直，OA⊥AK，作BK⊥AK于K，
设BK＝ycm，
∵四边形AKBH是矩形，
∴AH＝BK＝ycm，
∴OH＝OA﹣AH＝（75﹣y）cm，
∵BH2＝AB2﹣AH2＝OB2﹣OH2，
∴902﹣y2＝752﹣（75﹣y）2，
∴y＝54，
∴点B离地高度应小于54cm．

故答案为：75，54．
九．相似三角形的应用（共2小题）
10．（2023•平阳县一模）图1是一种机械装置，当滑轮P绕固定点O旋转时，点P在AB上滑动，带动点B绕固定点A旋转，使点C在水平杆MN上来回滑动．图2是装置的侧面示意图，AO⊥MN，OA＝10cm，AB＝18cm，BC＝12cm，OP＝6cm．当转动到OP′⊥AB′时，点C滑到最左边C′处，此时A，B′，C′恰好在同一条直线上，则点O到MN的距离是 　14　cm；当转动到OP′′⊥AB′′时，点C滑到最右边C′′处，则点C在MN上滑动的最大距离C′C′′＝　21.6　cm．

【答案】14；21.6．
【解答】解：延长AO交MN于点D，
∵OP′⊥AB′，AO⊥MN，
∴∠AP′O＝∠ADC′＝90°，
∵∠P′AO＝∠DAC′，
∴△P′AO∽△DAC′，
∴＝，
∵AB′＝AB＝18cm，B′C′＝BC＝12cm，A，B′，C′在同一条直线上，
∴C′A＝AB′+B′C′＝18+12＝30（cm），
∵∠AP′O＝90°，OA＝10cm，OP′＝OP＝6cm，
∴AP′＝＝＝8（cm），
∴＝，
解得OD＝14，
∴点O到MN的距离是14cm；
延长AB″交MN于点E，作B″F⊥MN于点F，
∵OP′⊥AC′，OP″⊥AE，OP′＝OP″，
∴点O在∠C′AE的平分线上，
∴∠DAE＝∠DAC′，
∵AD＝AD，∠ADE＝∠ADC′，
∴△ADE≌△ADC′（ASA），
∴EA＝C′A＝30cm，DE＝DC′，
∵AB″＝AB＝18cm，
∴B″E＝EA﹣AB″＝30﹣18＝12（cm），
∵B″C″＝BC＝12cm，
∴B″E＝B″C″，
∵∠ADE＝90°，EA＝30cm，AD＝OD+OA＝14+10＝24（cm），
∴DE＝＝＝18（cm），
∵B″F∥AD，
∵＝＝＝，
∴FC″＝FE＝DE＝×18＝7.2（cm），
∵C′E＝2DE＝2×18＝36（cm），C″E＝2FE＝2×7.2＝14.4（cm），
∴C′C″＝36﹣14.4＝21.6（cm），
故答案为：14；21.6．

11．（2023•瓯海区一模）甲、乙两幢完全一样的房子如图1，小聪与弟弟住在甲幢，为测量对面的乙幢屋顶斜坡M，N之间的距离，制定如下方案：两幢房子截面图如图2，AB＝12m，小聪在离屋檐A处3m的点G处水平放置平面镜（平面镜的大小忽略不计），弟弟在离点G水平距离3m的点H处恰好在镜子中看到乙幢屋顶N，此时测得弟弟眼睛与镜面的竖直距离IH＝0.6m．下楼后，弟弟直立站在DE处，测得地面点F与E，M，N在一条直线上，DE＝1.2m，FD＝2m，BF＝5m，则甲、乙两幢间距BC＝　25　m，乙幢屋顶斜坡M，N之间的距离为 　　m．


【答案】25，．
【解答】解：延长HG交CM于R，过N作NT⊥HR于T，如图：

根据题意得：△DEF∽△CMF，
∴＝，
∵CM＝AB＝12m，DE＝1.2m，FD＝2m，
∴＝，
解得CF＝20，
∵BF＝5m，
∴BC＝BF+CF＝25（m），
根据题意，∠EFD＝∠NMK，
∴tan∠EFD＝tan∠NMK，
∴＝，即＝，
∴MK＝NK，
设NK＝xm，则MK＝RT＝xm，NT＝NK+KT＝NK+AG＝（x+3）m，
∴GT＝GR+RT＝BC+RT＝（25+x）m，
根据反射定律可知，∠IGH＝∠NGT，
∵∠IHG＝90°＝∠T，
∴△IHG∽△NTG，
∴＝，即＝，
解得x＝3，
∴NK＝3m，MK＝5m，
在Rt△MNK中，
MN＝＝m，
故答案为：25，．