2022-2023学年湖南省永州市宁远县九年级（下）期中数学试卷（含解析）

2022-2023学年湖南省永州市宁远县九年级（下）期中数学试卷

一、选择题（本大题共10小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

1.  的绝对值是(    )

A.  B.  C.  D.

2.  一次函数与二次函数在同一平面直角坐标系中的图象可能是(    )

A.  B.
C.  D.

3.  新一代人工智能是推动科技跨越发展、产业优化升级、生产力整体跃升的驱动力量当前，我国人工智能领域呈现出技术创新和产业化应用双轮驱动、双向促进的发展特征根据中国信通院发布的最新数据测算，年我国人工智能核心产业规模达到亿元，同比增长，亿元用科学记数法表示为(    )

A.  B.  C.  D.

4.  已知的半径是，圆心到直线的距离是，则直线与的位置关系是(    )

A. 相离 B. 相交 C. 相切 D. 无法确定

5.  如图是由若干个相同的小正方体搭成的一个几何体分别从正面，左面，上面看到的形状图．则组成这个几何体的小正方体的个数为(    )

A.
B.
C.
D.

6.  抛物线的顶点坐标是(    )

A.  B.  C.  D.

7.  某学校组织开展手工制作实践活动，一学生制作的圆锥母线长为，底面圆的半径为，这个圆锥的侧面展开图的圆心角度数是(    )

A.  B.  C.  D.

8.  木箱里装有仅颜色不同的张红色和若干张蓝色卡片，随机从木箱里摸出张卡片记下颜色后再放回，经过多次的重复试验，发现摸到蓝色卡片的频率稳定在附近，则估计木箱中蓝色卡片有(    )

A. 张 B. 张 C. 张 D. 张

9.  如图，点，，均在上，若，则的度数是(    )

A.
B.
C.
D.

10.  某正方体的每个面上都有一个汉字，如图所示的是它的一种展开图，那么在原正方体中，与“诚”字所在面相对面上的汉字是(    )

A. 自
B. 信
C. 阳
D. 光

二、填空题（本大题共8小题，共32.0分）

11.  若式子在实数范围内有意义，则的取值范围是______．

12.  分解因式：          ．

13.  圆的内接正多边形中，正多边形的一条边所对的圆心角是，则正多边形的边数是______ ．

14.  二次函数的图象与轴交点坐标是______ ．

15.  一个圆锥的侧面展开图是半圆，则圆锥母线长与底面半径的比为______．

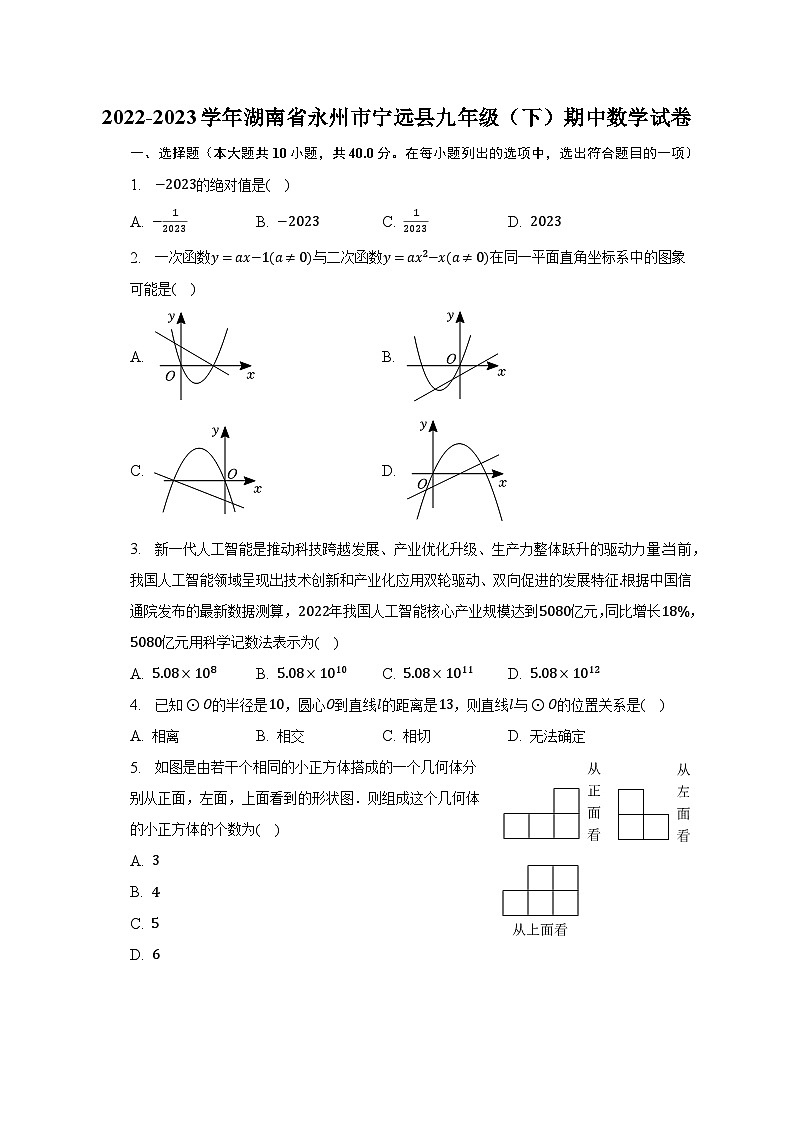
16.  如图，小芳和爸爸正在散步，爸爸身高，他在地面上的影长为若小芳比他爸爸矮，则她的影长为______

17.  “氢气在氧气中燃烧生成水”，这是______ 事件填“可能”、“不可能”、“必然”

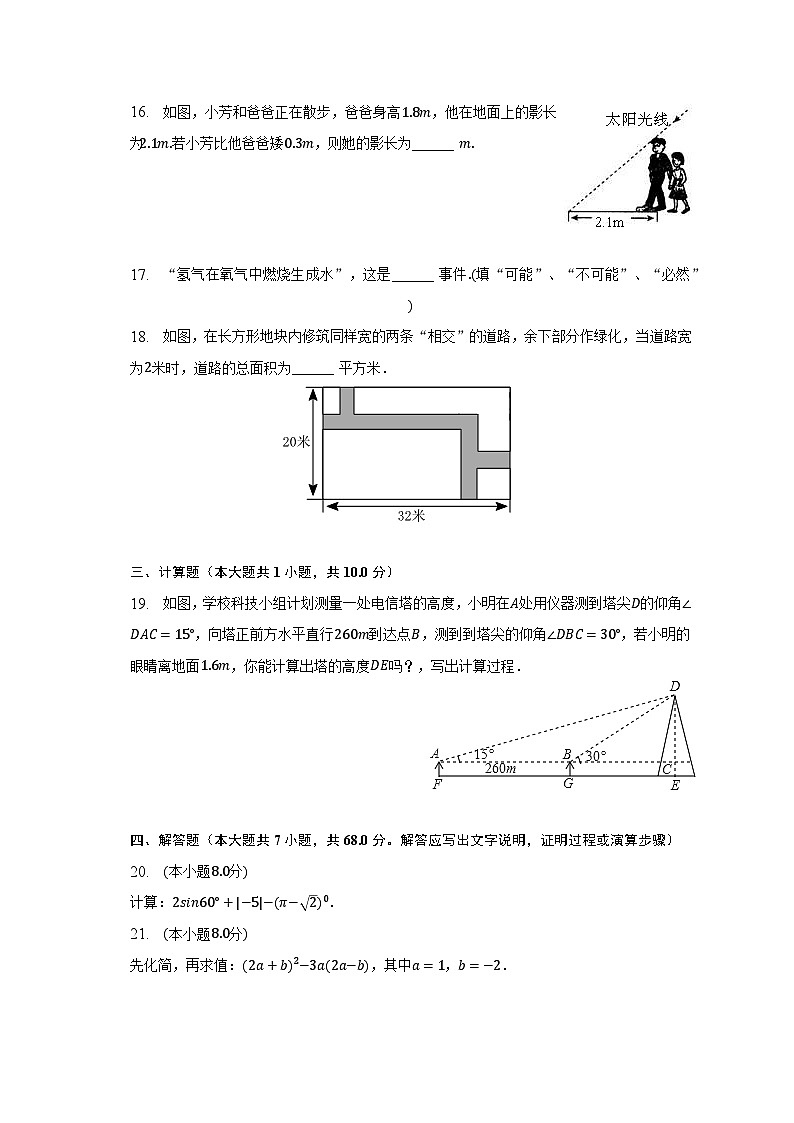
18.  如图，在长方形地块内修筑同样宽的两条“相交”的道路，余下部分作绿化，当道路宽为米时，道路的总面积为______ 平方米．

三、计算题（本大题共1小题，共10.0分）

19.  如图，学校科技小组计划测量一处电信塔的高度，小明在处用仪器测到塔尖的仰角，向塔正前方水平直行到达点，测到到塔尖的仰角，若小明的眼睛离地面，你能计算出塔的高度吗？，写出计算过程．

四、解答题（本大题共7小题，共68.0分。解答应写出文字说明，证明过程或演算步骤）

20.  本小题分
计算：．

21.  本小题分
先化简，再求值：，其中，．

22.  本小题分
新能源汽车已逐渐成为人们的交通工具，据某市某品牌新能源汽车经销商至月份统计，该品牌新能源汽车月份销售辆，月份销售辆．
求该品牌新能源汽车销售量的月均增长率；
若该品牌新能源汽车的进价为万元辆，售价为万元辆，则该经销商至月份共盈利多少万元？

23.  本小题分
月日是世界读书日，习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然正气”某校响应号召，开展了“读红色经典，传革命精神”为主题的读书活动，学校对本校学生五月份阅读该主题相关书籍的读书量进行了随机抽样调查，并对所有随机抽取的学生的读书量单位：本进行了统计根据调查结果，绘制了不完整的统计表和扇形统计图．

本次调查共抽取学生多少人？
表中的值为        ，扇形统计图中“本”部分所对应的圆心角的度数为        ．
已知该校有名学生，请估计该校学生中，五月份读书量不少于“本”的学生人数．

24.  本小题分
如图，为的直径，过圆上一点作的切线交的延长线于点，过点作交于点，连接．
直线与相切吗？并说明理由；
若，，求的长．

25.  本小题分
如图，在矩形中，，点是线段上的动点点不与点，重合，连接，过点作，交于点．
求证：∽；
如图，连接，过点作，垂足为，连接点是线段的中点，连接．
求的最小值；
当取最小值时，求线段的长．

 

26.  本小题分
如图一所示，在平面直角坐标中，抛物线经过点、，与轴交于点，顶点为点在线段上方的抛物线上有一动点，过点作于点，作交于点．
求抛物线和直线的函数表达式．
当的周长为最大值时，求点的坐标和的周长．
若点是抛物线上的一个动点，点是抛物线对称轴上的一个动点，是否存在以、、、为顶点的四边形为平行四边形？若存在，求出点的坐标，若不存在，请说明理由．

答案和解析

1.【答案】 

【解析】解：，
故选：．
根据绝对值的定义进行计算即可．
本题考查绝对值，理解绝对值的定义是正确解答的前提．
 

2.【答案】 

【解析】解：由，解得或，
一次函数与二次函数的交点为，，
A、由抛物线可知，，由直线可知，，故本选项错误，不符合题意；
B、由抛物线可知，，由直线可知，，由一次函数与二次函数可知，两图象交于点，则交点在轴的右侧，故本选项错误，不符合题意；
C、由抛物线可知，，由直线可知，，两图象的一个交点在轴上，另一个交点在第四选项，故本选项正确，符合题意；
D、由抛物线可知，，由直线可知，，的取值矛盾，故本选项错误，不合题意；
故选：．
可先由一次函数图象得到字母系数的正负，再与二次函数的图象相比较看是否一致．
本题考查了二次函数图象，一次函数的图象，应该熟记一次函数在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标等．
 

3.【答案】 

【解析】解：亿．
故选：．

用科学记数法表示较大的数时，一般形式为，其中，为整数，且比原来的整数位数少，据此判断即可．
此题主要考查了用科学记数法表示较大的数，一般形式为，其中，确定与的值是解题的关键．
 

4.【答案】 

【解析】解：的半径为，圆心到直线的距离是，而，
点到直线的距离大于半径，
直线与相离．
故选：．
运用直线与圆的三种位置关系，结合，即可解决问题．
本题考查的是直线与圆的位置关系，解决此类问题可通过比较圆心到直线距离与圆半径大小关系完成判定．
 

5.【答案】 

【解析】解：从主视图和俯视图可知，几何体的底层有个正方体，
从主视图和左视图可知，几何体的第二层有个正方体，
则搭成这个几何体的小正方体的个数为：，
故选：．
根据主视图和俯视图判断几何体的底层的正方体的个数，根据主视图和左视图判断几何体的第二和第三层的正方体的个数，计算即可．
本题考查的是由三视图判断几何体，掌握几何体的主视图、左视图和俯视图的概念是解题的关键．
 

6.【答案】 

【解析】解：是抛物线解析式的顶点式，
根据顶点式的坐标特点可知，顶点坐标为．
故选：．
已知解析式为抛物线的顶点式，可直接写出顶点坐标．
此题主要考查了求抛物线的顶点坐标的方法．利用解析式化为，顶点坐标是，对称轴是直线得出是解题关键．
 

7.【答案】 

【解析】解：设这种圆锥的侧面展开图的圆心角度数是，
根据题意得，，
解得，
即这种圆锥的侧面展开图的圆心角度数是，
故选：．
根据题意可知，圆锥的底面圆的周长扇形的弧长，即可列出相应的方程，然后求解即可．
本题考查圆锥的计算，解答本题的关键是明确圆锥的底面圆的周长扇形的弧长．
 

8.【答案】 

【解析】解：设木箱中蓝色卡片有张，根据题意得：
，
解得：，
经检验是原方程的解，
则估计木箱中蓝色卡片有张．
故选：．
根据蓝色卡片的频率可得摸到蓝色卡片的概率，根据概率公式即可求出蓝色卡片的数量．
本题主要考查利用频率估计概率，大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．
 

9.【答案】 

【解析】解：，
，
，
，
故选：．
先利用圆周角定理可得，然后再利用等腰三角形的性质，以及三角形内角和定理，进行计算即可解答．
本题考查了圆周角定理，熟练掌握圆周角定理是解题的关键．
 

10.【答案】 

【解析】解：正方体的平面展开图中，相对面的特点是之间一定相隔一个正方形，
在此正方体上与“诚”字相对的面上的汉字是“信”．
故选：．
正方体的平面展开图中，相对面的特点是之间一定相隔一个正方形，据此作答．
本题考查了正方体的展开图形，解题关键是从相对面入手进行分析及解答问题．
 

11.【答案】 

【解析】解：由题意得，，
解得．
故答案为：．
根据被开方数大于或等于列式计算即可得解．
本题考查的知识点为：二次根式有意义的条件，即二次根式的被开方数是非负数．
 

12.【答案】 

【解析】

【分析】
本题考查提公因式法与公式法的综合运用，一个多项式有公因式首先提取公因式，再用其他方法进行因式分解，同时因式分解要彻底，要分解到不能分解为止．先提出公因式，再运用平方差公式分解因式即可．
【解答】
解：．  

13.【答案】 

【解析】解：设正多边形的边数为．
由题意，
解得：．
故答案为：．
根据正多边形的中心角等于计算即可．
本题主要考查正多边形和圆的有关知识，牢记正多边形的中心角等于是解题的关键．
 

14.【答案】 

【解析】解：，当时，，
二次函数的图象与轴交点坐标是；
故答案为：．
求出二次函数，当时的值，即可得出答案．
本题考查了二次函数与坐标轴的交点；求出二次函数当时的值是解题的关键．
 

15.【答案】： 

【解析】解：设圆锥的母线长为，底面半径为，
圆锥的侧面展开图是一个半圆，
圆锥的侧面展开扇形的弧长为：，
圆锥的侧面展开扇形的周长等于圆锥的底面周长，
，
：：，
故答案为：：．
根据圆锥的侧面展开扇形的周长等于圆锥的底面周长，分别设出圆锥的母线长和圆锥的底面半径，利用上述关系得到关系式求出两者的比值即可．
本题考查了圆锥的计算，解题的关键是根据圆锥的侧面展开扇形的弧长等于圆锥的底面周长列出有关母线长和底面半径之间的关系式．
 

16.【答案】 

【解析】解：爸爸身高，小芳比他爸爸矮，
小芳高，
设小芳的影长为，
：：，
解得，
小芳的影长为．
根据实物与影子的比相等可得小芳的影长．
解决本题的关键是理解阳光下实物的影长与影子的比相等．
 

17.【答案】必然 

【解析】解：“氢气在氧气中燃烧生成水”一定会发生，这是必然事件．
根据事件发生的可能性判断相应类型即可．
解决本题需要正确理解必然事件、不可能事件、随机事件的概念．理解概念是解决这类基础题的主要方法．
解用到的知识点为：必然事件指在一定条件下一定发生的事件；不可能事件是指在一定条件下，一定不发生的事件；不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
 

18.【答案】 

【解析】解：平移后绿化地长为米，宽为米，
面积为平方米，
道路的总面积平方米．
故答案为：．
将“之”字路的水平线平移到上面，竖直线平移到右面，余下部分是一个长方形，得出长和宽即可．
本题主要考查了生活中的平移现象，利用平移的性质将绿化地部分组成一个矩形是解题的关键．
 

19.【答案】解：，
又，，
，
，
在中，，，
，
，
， 

【解析】首先证明，在中，利用直角三角形度角的性质，求出即可解决问题．
本题考查解直角三角形的应用仰角俯角问题，等腰三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
 

20.【答案】解：原式

． 

【解析】根据特殊角的三角函数值，绝对值的意义，零指数的意义计算即可．
本题考查了实数的运算，掌握特殊角的三角函数值，绝对值的意义，零指数的意义是解题的关键．
 

21.【答案】解：

，
当，时，
原式

． 

【解析】直接利用完全平方公式以及单项式乘多项式计算，进而合并同类项，把已知数据代入得出答案．
本题主要考查了整式的混合运算化简求值，掌握整式的混合运算化简求值运算法则是解题关键．
 

22.【答案】解：设新能源汽车销售量的月均增长率为，
根据题意，得，
所以，
解得，舍去，
，
答：该品牌新能源汽车月均增长率为．
经销商至月份共盈利：万元，
答：该经销商至月份共盈利万元． 

【解析】设新能源汽车销售量的月均增长率为，根据题意列出关于的一元二次方程，进行求解即可；
先求出月份销售汽车的辆数，从而求出个月销售总量，再根据每辆车的利润进行求解即可．
本题考查了一元二次方程的实际应用，明确题意，找出等量关系是解题的关键．
 

23.【答案】   

【解析】解：抽样调查的学生总数为：人，
答：本次调查共抽取学生人；
，
扇形统计图中“本”部分所对应的圆心角的度数为：，
故答案为：；；
人，
答：估计该校学生中，五月份读书量不少于“本”的学生人数为人．
由本人数及其所占百分比可得总人数；
用总人数分别减去其它读书量人数即可得出的值；用乘“本”所占百分比即可得出扇形统计图中“本”部分所对应的圆心角的度数；
总人数乘以样本中“读书量”不少于本的学生人数所占百分比即可．
本题考查了扇形统计图以及用样本估计总体，从统计图中得到必要的信息是解决问题的关键，扇形统计图直接反映部分占总体的百分比大小．
 

24.【答案】解：直线与相切，
理由是：连接，

切于，
，
即，
，
，
，
，，
，
在和中，
，
≌，
，
即，
过圆心，
直线与相切；

设的半径为，
在中，由勾股定理得：，
，
解得：，
，
，
，，，
，
解得：，
答：的长是． 

【解析】连接，根据切线的性质得出，根据平行线的性质求出，，求出，根据全等三角形的判定定理得出≌，根据全等三角形的性质得出，根据切线的判定定理证明即可；
设的半径为，根据勾股定理得出，求出，根据推出，代入求出即可．
本题考查了切线的性质和判定，直线与圆的位置关系，全等三角形的性质和判定，平行线的性质，勾股定理等知识点，能熟记切线的判定和性质定理是接此题的关键．
 

25.【答案】证明：四边形是矩形，
，
，
，
，
，
∽；
解：连接，如图，

，
是直角三角形，
点是的中点，
，
点在以点为圆心，为半径的圆上，
当，，三点不共线时，由三角形两边之和大于第三边得：，
当，，三点共线时，，
此时，取得最小值，
在中，，
的最小值为．
如图，过点作交于点，

∽，
，
设，则，
，
，
∽，
，
由可知的最小值为，
即，
又，
，
，
解得，
即，
由得，
设，则，
，
解得：或，
，，
或． 

【解析】由矩形的性质及直角三角形的性质证出，根据相似三角形的判定可得出结论；
连接，由直角三角形的性质得出，则点在以点为圆心，为半径的圆上，当，，三点共线时，，此时，取得最小值，由勾股定理求出，则可得出答案；
过点作交于点，证明∽，由相似三角形的性质得出，设，则，得出，证明∽，得出比例线段，列出方程，解得，求出，由得，设，则，得出方程，解得或，则可得出答案．

本题是相似形综合题，考查了矩形的性质，直角三角形的性质，相似三角形的判定与性质，三角形三边关系，勾股定理，熟练掌握相似三角形的判定与性质是解题的关键．
 

26.【答案】解：抛物线经过点、，
，
解得，
抛物线的解析式为，
令，可得，
，
设直线的解析式为，则，
，
直线的解析式为；

如图一中，连接，，设，

，，
，
，
，
，
，
是等腰直角三角形，，
的值最大时，的周长最大，



，
，
时，的面积最大，面积的最大值为，此时的值最大，
，
，
，
的周长的最大值，此时

存在．
理由：抛物线的解析式为，对称轴为直线，
如图二中，设，．

当为平行四边形的边时，则有，
解得或，
或，
当为平行四边形的对角线时，，
，
，
综上所述，满足条件的点的坐标为或或． 

【解析】利用待定系数法，把问题转化为方程组，求出，的值，设的解析式为，把，两点坐标代入求出，即可；
如图一中，连接，，设，证明是等腰直角三角形，求出的最大值，可得结论；
存在．如图二中，设，分两种情形：为平行四边形的边，为平行四边形的对角线，分别构建方程求解．
本题属于二次函数综合题，考查了二次函数的性质，一次函数的性质，平行四边形的判定和性质等知识，解题的关键是学会利用参数解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．