

安徽省淮南市凤台县2022-2023学年下学期八年级数学期末测试
展开淮南市凤台县2022-2023学年第二学期八年级数学期末测试
试题卷
注意事项:
1.你拿到的试卷满分为 150分,考试时间为 120分钟。
2.本试卷包括“试题卷”和“答题卷”两部分。 “试题卷”共4页,“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
4.考试结束后,请将“试题卷”和“答题卷”一并交回。
一、选择题(本大题共10小题,每小题4分,满分40分)
每小题都给出 A、B、C、D四个选项,其中只有一个是符合题目要求的.
1. 计算:
B.-5 C.3 D.5
2. 函数 的自变量 x的取值范围是
A. x>3 B. x≠4 C. x≠3 D. x≤4
3. 若 则以a. b. c为边的三角形是
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
4.如果最简二次根式 与 是同类二次根式,那么a的值是
A.5 B.3 C. -5 D. -3
5.在同一平面直角坐标系中,直线 y=5x+3 与直线 y=-2x-3的交点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6. 如图,在 Rt△ABC 中,∠C=90°,AC=8,BC=6,分别以点A,B为圆心,以AB长为半径画弧,两弧相交于点 D,连接AD,BD,则△ABD的周长为
A.18 B.24 C.12 D.30
7.某奶茶小店某月每日营业额(单位:元)中随机抽取部分数据,根据方差公式,得 则下列说法正确的是
A.样本的容量是4 B.该组数据的中位数是 400
C.该组数据的众数是 300 D. s²=6000
8. 如图,在矩形ABCD中,对角线 AC与BD相交于点O,点E,F是对角线 AC上的点.下列条件中,不能判定四边形 BEDF 是平行四边形的是
A. DE=BF B. AF=CE C.∠ABE=∠CDF D. DF∥BE
9. 若 则p的取值范围为
A.0<p<1 B.1<p<2 C.2<p<3 D.3<p<4
八年级数学(RJ)第八次(期末) 第1页
10. 如图,在菱形ABCD中,BC=4,∠B=120°,点E是AD的中点,点 F是 AB上一点,以EF为对称轴将△EAF 折叠得到△EGF,以CE为对称轴将△CDE 折叠得到△CHE,使得点 H落到EG上,连接 AG.下列结论错误的是
11. 小华调查了某地 1月份上旬的最低气温(单位:℃),分别是-2,0,3,-1,1,0,4,-3,-2,0,其中0℃以下(不含0℃)出现的频数是 .
12.如图,在▱ABCD中,AC=4,△ACD的周长为13,则▱ABCD 的周长为 .
13.如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB上一点,过点 E作DE⊥BC于点E,点O是CD的中点,连接 OA,OE,AE.若点 D是AB 的中点,AC=2,则AE的长为 .
14.在平面直角坐标系中,已知一次函数y=kx+b(k,b为常数且k≠0).
(1)当b=3k+6时,该函数恒经过一点,则该点的坐标为 ;
(2)当-2≤x≤2时,-8≤y≤4,则该函数的解析式为 .
三、(本大题共2小题,每小题8分,满分16分)
15.计算:
16.某商场为了了解A产品的销售情况,在上个月的销售记录中,随机抽取了5天 A产品的销售记录,其售价x(元/件)与对应销量 y(件)的全部数据如下表:
售价x(元/件) | 80 | 85 | 90 | 95 | 100 |
销量y(件) | 110 | 100 | 80 | 60 | 50 |
试求这5天中A产品平均每件的售价.
四、(本大题共2小题,每小题8分,满分 16分)
17.已知一次函数y=kx+b(k≠0)的图象经过(1,5)和(-1,1)两点.
(1)求这个一次函数的解析式;
(2)当x=-4时,求y的值.
八年级数学(RJ)第八次(期末) 第2页
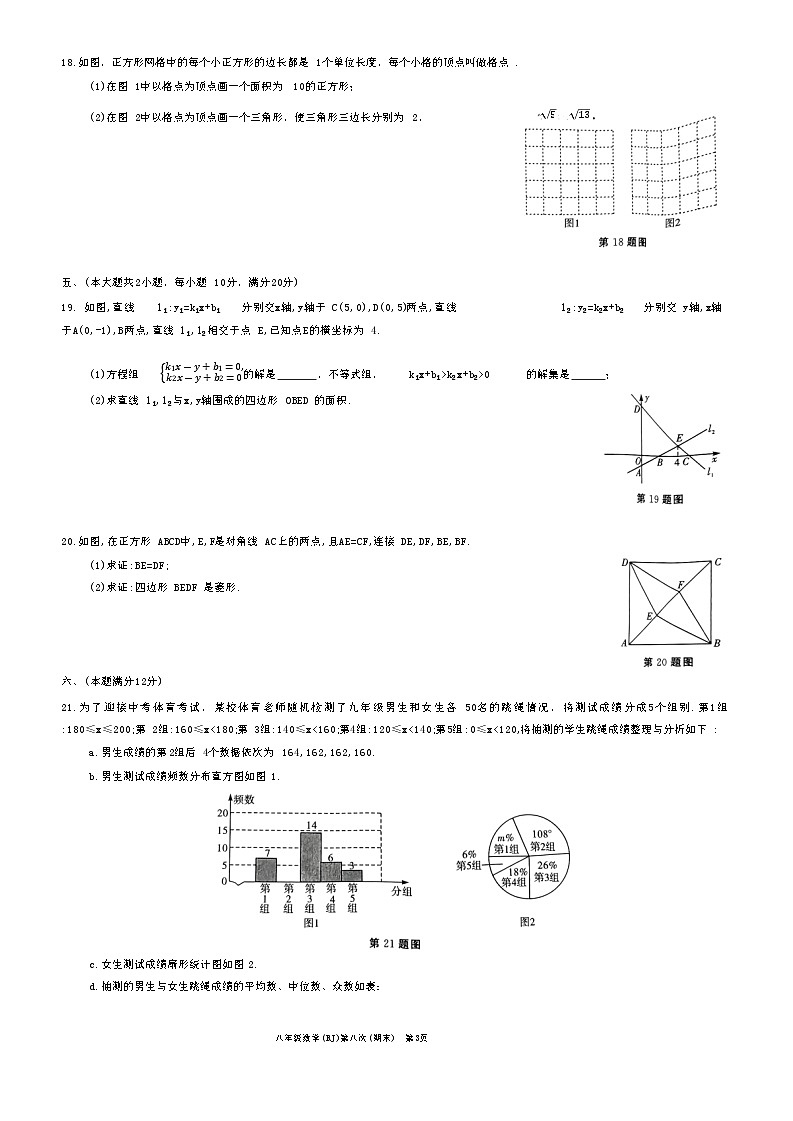
18.如图,正方形网格中的每个小正方形的边长都是1个单位长度,每个小格的顶点叫做格点.
(1)在图 1中以格点为顶点画一个面积为 10的正方形;
五、(本大题共2小题,每小题 10分,满分20分)
19. 如图,直线 l₁:y₁=k₁x+b₁ 分别交x轴,y轴于 C(5,0),D(0,5)两点,直线 l₂:y₂=k₂x+b₂ 分别交 y轴,x轴于A(0,-1),B两点,直线 l₁,l₂相交于点 E,已知点E的横坐标为 4.
(1)方程组 的解是 ,不等式组, k₁x+b₁>k₂x+b₂>0 的解集是 ;
20.如图,在正方形 ABCD中,E,F是对角线 AC上的两点,且AE=CF,连接 DE,DF,BE,BF.
六、(本题满分12分)
21.为了迎接中考体育考试,某校体育老师随机检测了九年级男生和女生各 50名的跳绳情况,将测试成绩分成5个组别.第1组:180≤x≤200;第 2组:160≤x<180;第 3组:140≤x<160;第4组:120≤x<140;第5组:0≤x<120,将抽测的学生跳绳成绩整理与分析如下:
a.男生成绩的第2组后 4个数据依次为 164,162,162,160.
b.男生测试成绩频数分布直方图如图1.
c.女生测试成绩扇形统计图如图2.
d.抽测的男生与女生跳绳成绩的平均数、中位数、众数如表:
八年级数学(RJ)第八次(期末) 第3页
性别 | 平均数 | 中位数 | 众数 |
男生 | 162.6 | n | 166 |
女生 | 162.6 | 159 | 164 |
请根据以上信息,解答下列问题:
(1)m= ,n= ,并补全频数分布直方图;
(2)根据上述成绩数据的分析,你认为男生与女生哪个跳绳成绩更好,并说明理由(写出一条理由即可);
(3)已知每分钟跳绳成绩达到 160个,成绩为优秀等级.若该校九年级男生有 500名,女生有 600名,请估计该校九年级学生跳绳成绩达到优秀等级的学生数.
七、(本题满分 12分)
22.某幼儿园计划购进一批小桌子和小椅子,数量共有50个,某商家给出的内部价如下表:
| 小桌子 | 小椅子 |
进价(元/个) | 100 | 60 |
售价(元/个) | 130 | 100 |
设该商家所获利润为 y(单位:元),幼儿园购进小桌子的个数为x(单位:个).
(1)请写出y与x之间的函数解析式(不要求写出x的取值范围);
(2)该幼儿园购进这批小桌子和小椅子的资金控制在 6000元以内,请你设计一种购进方案使得幼儿园尽可能多的购进小桌子且使得该商家利润最小,并求最小利润.
八、(本题满分 14分)
23.如图1,在四边形 ABCD中,AB=CD,AD=BD=BC,∠ADB=90°,点E是AB的中点,点 F 是△ABD内一点,连接 AF,DF,EF,∠AFD=90°.
(1)若∠BDF=20°,求∠EAF的度数;
(2)探索 AF,DF 和 EF之间的数量关系,并说明理由;
(3)如图 2,利用(2)中结论,已知 ,求CD的长.
八年级数学(RJ)第八次(期末) 第4页
参考答案
一、1. D 2. B 3. B 4. B 5. C 6. D 7. C 8. A 9. A 10. D
10.[提示]由折叠可知 EF 和CE分别是∠AEG 和∠DEG 的平分线.
又∵∠AED=180°,
选项 A正确.
又∵点A 与点G关于 EF 对称,
∴EF⊥AG.
∴CE∥AG,选项 B正确.
如答图,过点 C作CM⊥AB于点M.
∴CF=FG+CG=4-a+4=8-a.
∵FM²+CM²=CF²,
解得a=2.4.
∴FG=4-2.4=1.6,CF=8-a=8-2.4=5.6.
选项 C正确,选项 D错误.
综上,故选 D.
二、11. 4 12. 18 14. (1)(-3,6)(2分) (2)y=3x-2或y=-3x-2(3分)
13. [提示]∵DE⊥BC,
∴△CDE 是直角三角形.
在 Rt△ACD和 Rt△CDE中,OA 和OE 分别是斜边上的中线,
∴OA=OE.
∵∠BAC=90°,AB=AC,
∴△ABC 是等腰直角三角形,
∴∠ACE=45°.
∵OA=OC=OE,
∴∠AOE=2∠ACO+2∠ECO=2∠ACE=2×45°=90°.
∴△AOE 是等腰直角三角形.
∵点 D是AB的中点,AC=2,
14. [提示](1)把b=3k+6代入函数解析式中,得 y=kx+3k+6.
当x=-3时,y=6,故该函数恒经过点(-3,6).
(2)当k>0时,易知该函数图象经过点(-2,-8)和(2,4),代入函数解析式中,得
解得
此时该函数的解析式为 y=3x-2.
当k<0时,易知该函数图象经过点(-2,4)和(2,-8),代入函数解析式中,得
解得
此时该函数的解析式为 y= -3x-2.
综上,该函数的解析式为y=3x-2或y=-3x-2.
三、15. 解:原式 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
=-4……………………………………………………………………………………………………………………………………………………………………………………………………………………………8分
16. 解:总销量为 110+100+80+60+50=400(件).
总销售额为 110×80+100×85+80×90+60×95+50×100=35200(元).
35200÷400=88(元).
答:这5天中A产品平均每件的售价为88元………………………………………………………………………8分
四、17.解:(1)把(1,5)和(-1,1)两点坐标代入 y=kx+b中,得
………………………………………………………………………………………………………………………………………………………………………………………………………………………………3分
解得
∴一次函数的解析式为y=2x+3…………………………………………………………………………………………………6分
(2)当x=-4时,y=2x(-4)+3=-5.
∴当x=-4时,y的值为-5…………………………………………………………………………………………………………………………8分
18.(1)正方形如图1所示……………………………………………………………………………………………………………………………………………………………4分
(图形位置不唯一)
(2)三角形如图2所示………………………………………………………………………………………………………………………………………………………………………………8分
(图形位置不唯一)
五、19. ……………………………………………………………………………………………………………………………………………………………………………………………………………4分
(2)解:把点 C,D的坐标分别代入直线 l₁:y₁=k₁x+b₁, 得
解得
∴直线 l₁ 的解析式为 y₁=-x+5.
当x=4时,y₁=1,故点E(4,1)……………………………………………………………………………………………………………6分
把点A,E的坐标分别代入直线 l₂:y₂=k₂x+b₂,得
解得
∴直线 l₂的解析式为
当y=0时,即 解得x=2,故点B(2,0)…………………………………………………………………………………………………………8分
∴BC=OC-OB=5-2=3.
………………………………………………………………………………………………………………………10分
20. (1)证明:∵四边形ABCD是正方形,AC 是其对角线,
∴AB=CD,∠BAE=∠DCF=45°.
又∵AE=CF,
∴△ABE≌△CDF(SAS).
∴BE=DF……………………………………………………………………………………………………………………………………………………………………………………………………………………5分
六、21.(1)20162补全的频数分布直方图如下:…………………………………………………………………4分
(2)男生跳绳成绩更好……………………………………………………………………………………………………………………………………………………………………………6分
理由:因为男生、女生跳绳成绩的平均数相同,男生跳绳成绩的中位数、众数均大于女生,所以男生跳绳成绩更好…8分
(人).
答:估计该校九年级学生跳绳成绩达到优秀等级的学生有570人……………………………………12分
七、22.解:(1)商家所获利润为 y元,幼儿园购进小桌子x个,则购进小椅子(50-x)个,根据题意,得
y=(130-100)x+(100-60)(50-x)=-10x+2000………………………………………………………3分
∴y与x之间的函数解析式为y=-10x+2000………………………………………………………………6分
(2)幼儿园购进小桌子x个,则购进小椅子(50-x)个,根据题意,得
130x+100(50-x)≤6000………………………………………………………………………………………………………………………………………………8分
解得 ………………………………………………………………………………………………………………………………………………………………………………………………………………10分
又∵函数 y=-10x+2000的一次项系数-10<0,
∴y随x的增大而减小.
∴当x=33时,y有最小值,最小值为-10×33+2000=1670(元).
答:当x=33时,该商家利润最小,最小利润为1670元…………………………………………………12分
八、23. 解:(1)∵AD=BD,∠ADB=90°,
∴∠BAD=45°.
∵∠AFD=90°,
∴∠DAF+∠ADF=90°.
又∵∠BDF+∠ADF=90°,∠BDF=20°,
∴∠BDF=∠DAF=20°.
∴∠EAF=∠BAD-∠DAF=45°-20°=25°.…………………………………………………………………4分
理由如下:⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
如答图,连接 DE,过点 E作EG⊥EF交AF 于点G.
∴∠AED-∠DEG=∠GEF-∠DEG,即∠AEG=∠DEF.
由(1)可知∠BDF=∠DAF,
∴∠BAD-∠DAF=∠BDE-∠BDF,即∠EAG=∠EDF.
∵∠AEG=∠DEF,AE=DE,∠EAG=∠EDF,
∴△AEG≌△DEF(ASA).
∴EG=EF,AG=DF.
∴△EFG 是等腰直角三角形.
……………………………………………………………………………………………………………………………………………………………………………………10分
(3)∵AB=CD,AD=BC,
∴四边形 ABCD是平行四边形.
……………………………………………………………………………………………………………………………………………………………………14分
2022-2023学年安徽省淮南市凤台县八年级(下)期末数学试卷(含解析): 这是一份2022-2023学年安徽省淮南市凤台县八年级(下)期末数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
安徽省淮南市凤台县2022-2023学年下学期八年级数学期末测试(含答案): 这是一份安徽省淮南市凤台县2022-2023学年下学期八年级数学期末测试(含答案),共11页。
安徽省淮南市凤台县2022-2023学年下学期八年级数学期末测试题: 这是一份安徽省淮南市凤台县2022-2023学年下学期八年级数学期末测试题,共8页。












