




浙江省杭州市余杭区2022-2023学年八年级下学期5月 数学独立作业
展开八年级数学独立作业
一、选择题:本大题有10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项最符合题目要求.
1.若在实数范围内有意义,则x的取值范围是(▲)
A.x>2 B.x≥2 C.x≤2 D.x≠2
2.下列各式中的最简二次根式是(▲)
A. B. C. D.
3.用配方法解方程x2+4x-3=0,正确的是(▲)
A.(x-1)2=3 B.(x+1)2=3 C.(x+2)2=7 D.(x-2)2=7
4.“求证:Rt△ABC的两个锐角∠A,∠B中至少有一个不大于45°.” 用反证法证明这个命题时,应先假设(▲)
A.∠A>45°,∠B>45° B.∠A≥45°,∠B≥45°
C.∠A<45°,∠B<45° D.∠A≤45°,∠B≤45°
5.两年前,某校七(1)班的学生平均年龄为13岁,方差为3,若学生没有变动,则今年升为九(1)班的学生年龄中平均年龄和方差分别为(▲)
A.13岁,改变 B.15岁,不变 C.15岁,改变 D.不变,不变
6.如图,长30m,宽20m的矩形基地上有三条宽x m的小路,剩余522m2种花,依题意列方程(▲)
A.20x+30×2x=600-522
B.20x+30×2x-x2=600-522
C.(20-2x)(30-x)=522
D.(20-x)(30-2x)=522
7.下列方程中,有两个相等实数根的是(▲)
A.(x-1)(x+1)=0 B.(x-1)(x-1)=0 C.(x-1)2=4 D.x(x-1)=0
8.如图,△ABC中,D是BC边的中点,AE平分∠BAC,BE⊥AE于E,已知AB=10,AC=18,则DE的长为(▲)
A.4 B.5 C.6 D.7
第8题图 第9题图
八年级数学 第1页 共4页
9.如图,正方形ABCD中,点E是AB中点,点F在BC边上,点B关于EF的对称点为B',连接B'D,B'E,B'F.若ABCD的边长为2,当四边形BEB'F是正方形时,B'D=(▲)
A. B. C. D.3
10.在ABCD中,O为AC的中点,点E,M为AD边上
任意两个不重合的动点(不与端点重合),EO的延长线与
BC交于点F,MO的延长线与BC交于点N.
有四个推断:
①EF=MN;
②EN∥MF;
③若ABCD是菱形,则至少存在一个四边形ENFM是菱形;
④对于任意的ABCD,存在无数个四边形ENFM是矩形.正确的是(▲)
A.①③ B.②③ C.①④ D.②④
二、填空题:本题有6个小题,每小题4分,共24分.
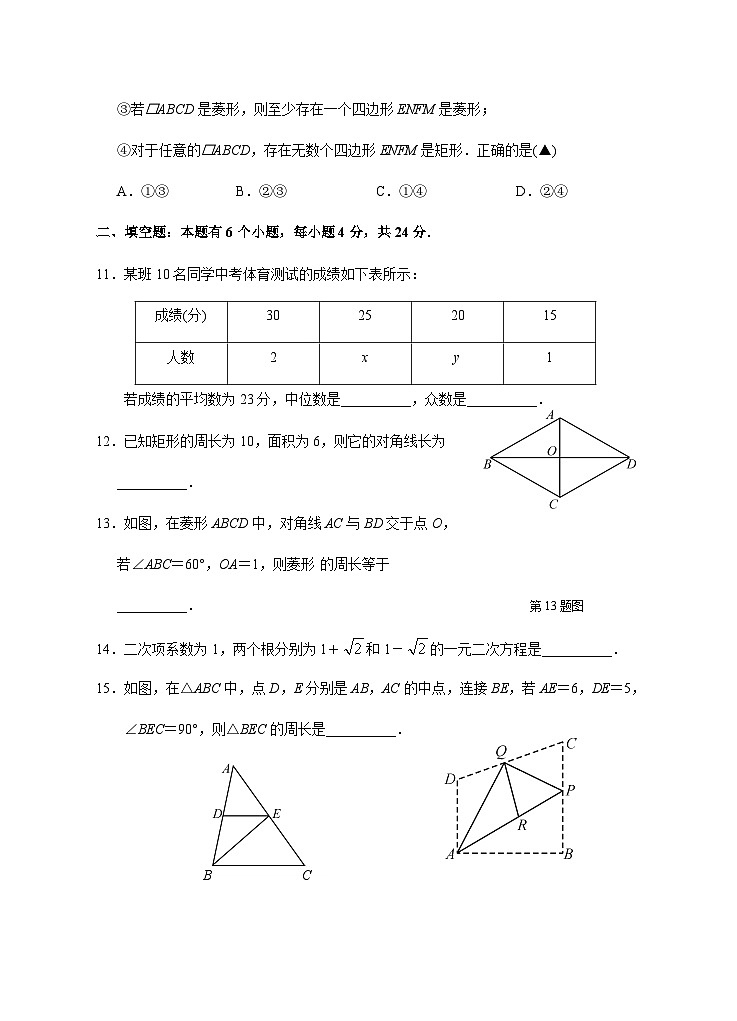
11.某班10名同学中考体育测试的成绩如下表所示:
成绩(分) | 30 | 25 | 20 | 15 |
人数 | 2 | x | y | 1 |
若成绩的平均数为23分,中位数是__________,众数是__________.
12.已知矩形的周长为10,面积为6,则它的对角线长为
__________.
13.如图,在菱形ABCD中,对角线AC与BD交于点O,
若∠ABC=60°,OA=1,则菱形 的周长等于
__________. 第13题图
14.二次项系数为1,两个根分别为1+和1-的一元二次方程是__________.
15.如图,在△ABC中,点D,E分别是AB,AC的中点,连接BE,若AE=6,DE=5,
∠BEC=90°,则△BEC的周长是__________.
第15题图 第16题图
16.如图,将四边形纸片ABCD沿过点A的直线折叠,使得点B落在CD上的点Q处.折 痕为AP;再将△PCQ,△ADQ分别沿PQ,AQ折叠,此时点C,D落在AP上的同一 点R处.∠PAQ=__________°;若四边形APCD是平行四边形,则的值为__________.
八年级数学 第2页 共4页
三、解答题:本题有7小题,共66分.解答应写出文字说明、证明过程或演算步骤.
17.(本题满分6分)
化简或计算:
(1); (2)×÷.
18.(本题满分8分)
解方程:
(1)x2-8x-2=0; (2)2x2-x-3=0.
19.(本题满分8分)
一高尔夫球手某次击出一个高尔夫球的高度h(m)和经过的水平距离d(m)可用公式
h=d-0.01d2来估计.
(1)当球的水平距离达到50m时.球上升的高度是多少?
(2)当球的高度第一次达到16m时.球的水平距离是多少?
20.(本题满分10分)
某区举办中学生科普知识竞赛,各学校分别派出一支代表队参赛.知识竞赛满分为100分,规定85分及以上为“合格”,95分及以上为“优秀”.现将A,B两个代表队的竞赛成绩统计表及分布图展示如下:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
A队 | 88 | 90 | 61 | 70% | 30% |
B队 | a | b | 71 | 75% | 25% |
(1)求出成绩统计表中a,b的值.
(2)小明的成绩虽然在本队排名属中游,但是竞赛成绩低于本队的平均分,那么小明应属于哪个队?请说明理由.
(3)从平均分、合格率、优秀率、队内成绩的整齐性等方面进行综合评价,你认为集体奖应该颁给哪一队?
八年级数学 第3页 共4页
21.(本题满分10分)
已知一元二次方程mx2+nx-(m+n)=0.
(1)求证:该方程有两个实数根.
(2)若方程的两根x1,x2满足x1•x2>1,n=1,求m的取值范围.
22.(本题满分12分)
如图,在ABCD中,点E在BC边上,AE平分∠BAD,点F在AD边上,EF∥AB.
(1)求证:四边形ABEF是菱形.
(2)若AB=2,BC=3,点P在线段AE上运动,请直接回答当点P在什么位置时PC+PF取得最小值,最小值是多少?
23.(本题满分12分)
如图,正方形ABCD中,E是对角线BD上一点,连接AE,过点E作EF⊥AE,交直线CB于点F.
(1)如图1,点F在线段BC上.
①若∠BAE=α,直接写出∠BFE的大小(用含α的式子表示);
②求EA与EF的数量关系,并说明理由.
(2)如图2,点F在线段CB的延长线上.求线段BC,BE和BF的等量关系,并说明理由.
图1 图2
八年级数学 第4页 共4页
浙江省杭州市临平区2023-2024学年八年级下学期3月独立作业数学试题(含解析): 这是一份浙江省杭州市临平区2023-2024学年八年级下学期3月独立作业数学试题(含解析),共15页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙江省杭州市临平区2023-2024学年八年级下学期3月独立作业数学试题: 这是一份浙江省杭州市临平区2023-2024学年八年级下学期3月独立作业数学试题,共4页。
浙江省杭州市余杭区、临平区、富阳区等多区联考2022-2023学年八年级上学期12月独立作业数学试卷(含答案): 这是一份浙江省杭州市余杭区、临平区、富阳区等多区联考2022-2023学年八年级上学期12月独立作业数学试卷(含答案),共7页。












