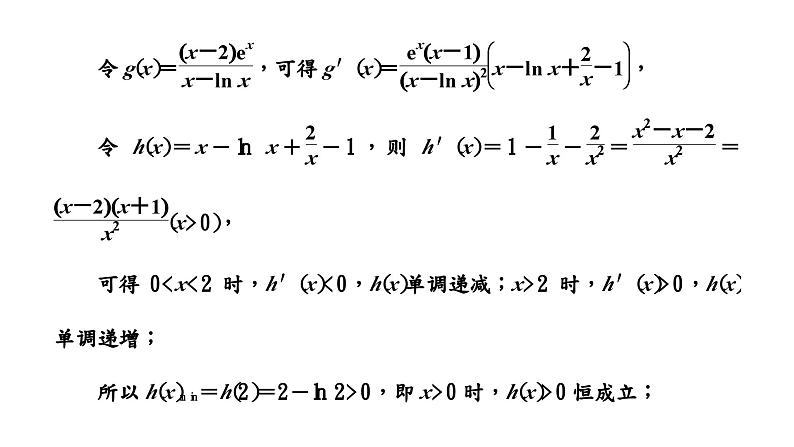
2024年新高考数学一轮复习 第三章 第三节 第四课时 题型精研——利用导数研究函数的零点问题

课时跟踪检测(二十三) 题型精研——利用导数研究函数的零点问题

1．(2023·梅州模拟)已知f(x)＝ex－2x.

(1)求f(x)的单调区间；

(2)证明：方程f(x)＝cos x在无实数解．

解：(1)f(x)的定义域为R，f′(x)＝ex－2，

令f′(x)>0，即ex>2，解得x>ln 2，

令f′(x)<0，即ex<2，解得x<ln 2.

综上，f(x)的单调递减区间为(－∞，ln 2)，单调递增区间为(ln 2，＋∞)．

(2)证明：令g(x)＝ex－2x－cos x，x∈，g′(x)＝ex＋sin x－2，

因为当x∈时，g′(x)＝(ex－1)＋(sin x－1)<0，

所以g(x)在单调递减．

所以g(x)>g(0)＝0，

所以函数g(x)在无零点．

即方程f(x)＝cos x在无实数解．

2．(2021·全国甲卷)已知a＞0且a≠1，函数f(x)＝(x＞0)．

(1)当a＝2时，求f(x)的单调区间．

(2)若曲线y＝f(x)与直线y＝1有且仅有两个交点，求a的取值范围．

解：(1)当a＝2时，f(x)＝，则f′(x)＝＝＝.

∴当x∈时，f′(x)＞0；当x∈时，f′(x)＜0.即f(x)的单调递减区间为，单调递增区间为.

(2)要使曲线y＝f(x)与直线y＝1有2个交点，

即＝1有2个解，则＝有2个解．

令g(x)＝(x＞0)，则g′(x)＝(x＞0)．

令g′(x)＝＝0，解得x＝e.

令g′(x)＞0，解得0＜x＜e，此时g(x)单调递增；

令g′(x)＜0，解得x＞e，此时g(x)单调递减．

故g(x)max＝g(e)＝.

而g(x)在x＞e时，g(x)∈.

又∵g(1)＝0，∴要使条件成立，则0＜＜.

易得a∈(1，e)∪(e，＋∞)．

3．(2023·遵义模拟)已知函数f(x)＝ln x－ax＋1，a∈R.

(1)当a＝1时，求函数f(x)的单调区间；

(2)若f(x)＝1有且仅有两个不相等实根，求实数a的取值范围．

解：(1)当a＝1时，f(x)＝ln x－x＋1，定义域为x∈(0，＋∞)，

f′(x)＝－1＝，当x∈(0,1)时，f′(x)>0；

当x∈(1，＋∞)时，f′(x)<0，所以函数f(x)的单调递增区间为(0,1)，单调递减区间为(1，＋∞)．

(2)由题意，ln x－ax＋1＝1，即a＝有且仅有两个不相等实根，令g(x)＝，h(x)＝a，

即g(x)与h(x)的图象有两个交点，

g′(x)＝，x∈(0，e)时，g′(x)>0，x∈(e，＋∞)时，g′(x)<0，

所以g(x)在(0，e)单调递增，在(e，＋∞)单调递减，

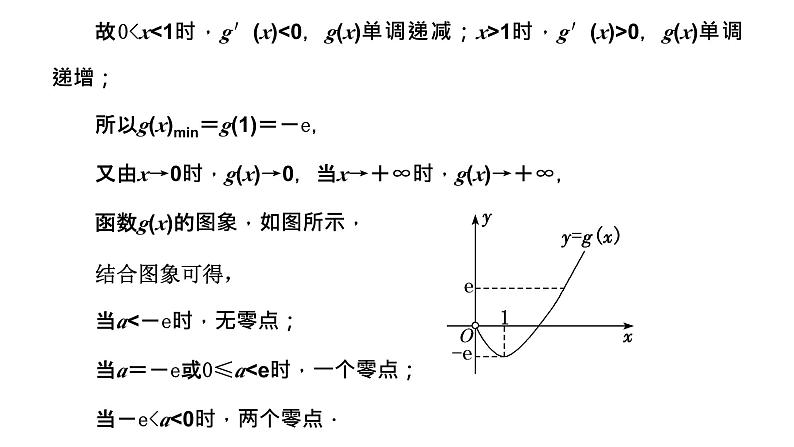
所以函数g(x)的最大值为g(e)＝＝，

又因为x→0时，g(x)→－∞，x→＋∞时，g(x)→0，

所以当a∈时，g(x)与h(x)的图象有两个交点，所以实数a的取值范围为.

4．(2022·唐山二模)已知函数f(x)＝，g(x)＝bsin x，曲线y＝f(x)和y＝g(x)在原点处有相同的切线l.

(1)求b的值以及l的方程；

(2)判断函数h(x)＝f(x)－g(x)在(0，＋∞)上零点的个数，并说明理由．

解：(1)依题意得，f′(x)＝，g′(x)＝bcos x.

∴f′(0)＝g′(0)＝b＝1，∴b＝1，l的方程为y＝x.

(2)由已知得，h(x)＝－sin x，当x>时，＝3－>1≥sin x，h(x)>0，此时h(x)无零点．

当0<x<时，h′(x)＝－cos x，

令H(x)＝－cos x，x∈，

则H′(x)＝－＋sin x，显然H′(x)在上单调递增，

又H′(0)＝－<0，H′>0，所以存在t∈使得H′(t)＝0，

因此可得0<x<t时，H′(x)<0，H(x)单调递减；

t<x<时，H′(x)>0，H(x)单调递增．又H(0)＝0，H>0，

所以存在λ∈，使得H(λ)＝0，

即0<x<λ时，H(x)<0，h′(x)<0，h(x)单调递减；

λ<x<时，H(x)>0，h′(x)>0，h(x)单调递增．

又h(0)＝0，h>0，所以h(x)在上有一个零点．

综上，h(x)在(0，＋∞)上有1个零点．