2023年江苏省连云港市海州区新海实验中学中考数学三模试卷（含答案）

这是一份2023年江苏省连云港市海州区新海实验中学中考数学三模试卷（含答案），共31页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2023年江苏省连云港市海州区新海实验中学中考数学三模试卷
一、选择题（本大题共8小题，共24.0分。在每小题列出的选项中，选出符合题目的一项）
1. 实数-2023的绝对值是(    )
A. 2023 B. -2023 C. 12023 D. -12023
2. 下列各式中，计算错误的是(    )
A. (-a)-1=1a B. a3⋅a4=a7 C. (2a2)3=8a6 D. a3÷a2=a
3. 已知一组数据：3，-2，4，-3，0，-4，2，这组数据的平均数和极差分别是(    )
A. 0，8 B. -1，7 C. 0，7 D. -1，8
4. 函数y= x+1x的自变量的取值范围是(    )
A. x≥-1 B. x≥-1且x≠0 C. x>0 D. x>-1且x≠0
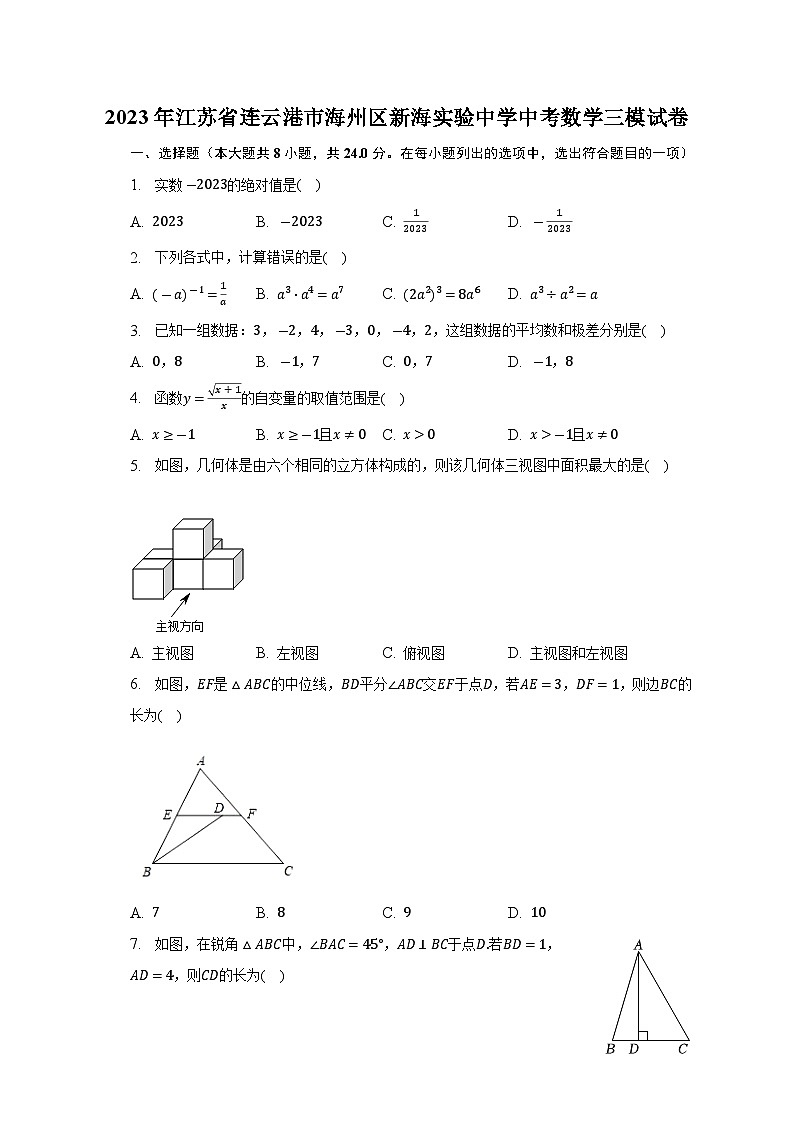
5. 如图，几何体是由六个相同的立方体构成的，则该几何体三视图中面积最大的是(    )


A. 主视图 B. 左视图 C. 俯视图 D. 主视图和左视图
6. 如图，EF是△ABC的中位线，BD平分∠ABC交EF于点D，若AE=3，DF=1，则边BC的长为(    )

A. 7 B. 8 C. 9 D. 10
7. 如图，在锐角△ABC中，∠BAC=45°，AD⊥BC于点D.若BD=1，AD=4，则CD的长为(    )
A. 3
B. 2
C. 5
D. 2.4
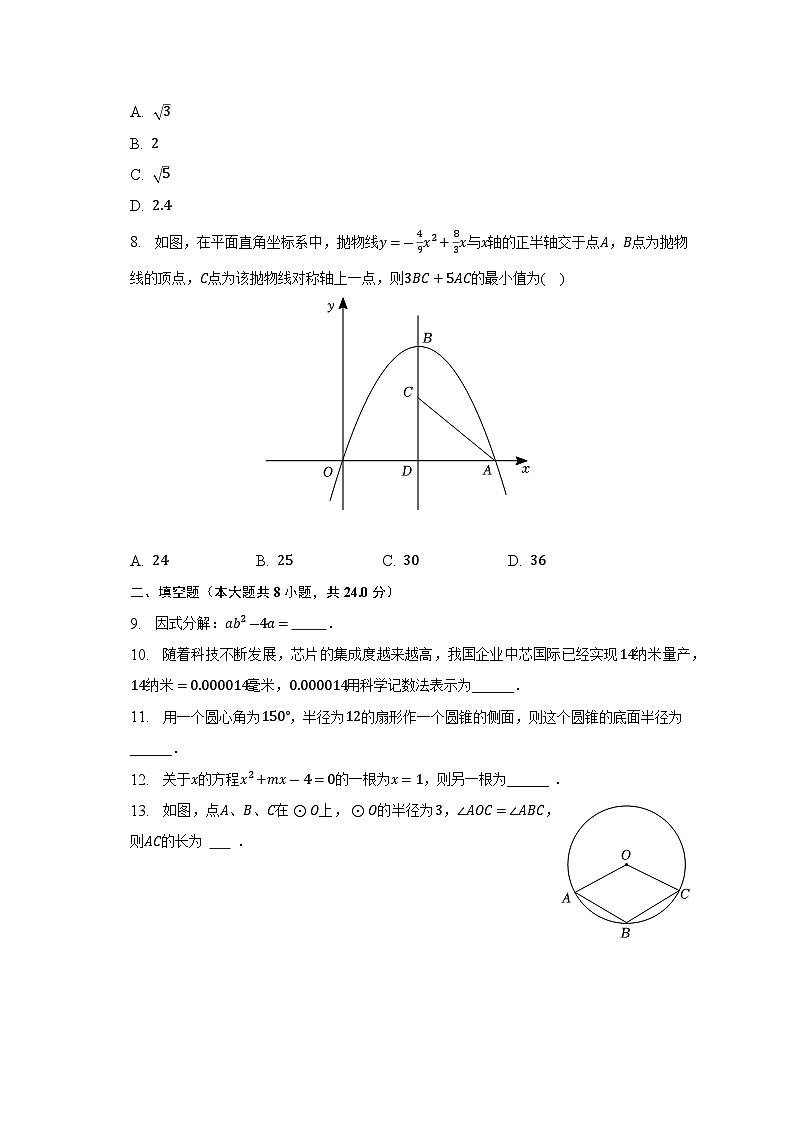
8. 如图，在平面直角坐标系中，抛物线y=-49x2+83x与x轴的正半轴交于点A，B点为抛物线的顶点，C点为该抛物线对称轴上一点，则3BC+5AC的最小值为(    )

A. 24 B. 25 C. 30 D. 36
二、填空题（本大题共8小题，共24.0分）
9. 因式分解：ab2-4a=          ．
10. 随着科技不断发展，芯片的集成度越来越高，我国企业中芯国际已经实现14纳米量产，14纳米=0.000014毫米，0.000014用科学记数法表示为______．
11. 用一个圆心角为150°，半径为12的扇形作一个圆锥的侧面，则这个圆锥的底面半径为______．
12. 关于x的方程x2+mx-4=0的一根为x=1，则另一根为______ ．
13. 如图，点A、B、C在⊙O上，⊙O的半径为3，∠AOC=∠ABC，则AC的长为        ．


14. 已知反比例函数y=k2x(k≠0)的图象过点A(a,y1)，B(a+1,y2)，若y2>y1，则a的取值范围为______．
15. 如图，将半径为4，圆心角为120°的扇形AOB绕点B逆时针旋转60°，得到扇形O'A'B，其中点A的运动路径为AA'，则图中阴影部分的面积和为______ ．


16. 如图，在△ABC中，AB=AC=5，BC=8，D是BC边上一点，且BD=AB.E是AB延长线上一点，连接ED交AC于F，若∠ADE=∠B，则EF的长度为______ ．


三、解答题（本大题共11小题，共102.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题6.0分)
计算：(-1)2023+| 2-2|-2cos45°+ 8
18. (本小题6.0分)
解不等式组x+2≥2x-13x+12-1>x-2，并写出解集中的整数解．
19. (本小题6.0分)
先化简，再求值：(1-1x-1)÷x-2x2-1，其中x是方程x2-2x-3=0的根．
20. (本小题8.0分)
以人工智能、大数据、物联网为基础的技术创新促进了新业态蓬勃发展，新业态发展对人才的需求更加旺盛.某大型科技公司上半年新招聘软件、硬件、总线、测试四类专业的毕业生，现随机调查了m名新聘毕业生的专业情况，并将调查结果绘制成如图两幅不完整的统计图．

请根据统计图提供的信息，解答下列问题．
(1)m= ______ ；n= ______ ．
(2)补全条形统计图：在扇形统计图中，“软件”所对应的扇形的圆心角是______ 度；
(3)若该公司新招聘600名毕业生，请估计“总线”专业的毕业生有多少名．
21. (本小题10.0分)
为弘扬中华民族传统文化，某市举办了中小学生“国学经典大赛”，比赛项目为：A.唐诗；B.宋词；C.论语；D.三字经．比赛形式分“单人组”和“双人组”．
(1)小华参加“单人组”，他从中随机抽取一个比赛项目，恰好抽中“论语”的概率是多少？
(2)小明和小红组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次．则恰好小明抽中“唐诗”且小红抽中“宋词”的概率是多少？小明和小红都没有抽到“三字经”的概率是多少？请用画树状图或列表的方法进行说明．
22. (本小题10.0分)
某快递公司为了加强疫情防控需求，提高工作效率，计划购买A、B两种型号的机器人来搬运货物，已知每台A型机器人比每台B型机器人每天少搬运10吨，且A型机器人每天搬运540吨货物与B型机器人每天搬运600吨货物所需台数相同．
(1)求每台A型机器人和每台B型机器人每天分别搬运货物多少吨？
(2)每台A型机器人售价1.2万元，每台B型机器人售价2万元，该公司计划采购A、B两种型号的机器人共30台，必须满足每天搬运的货物不低于2820吨，购买金额不超过48万元．
请根据以上要求，完成如下问题：
①设购买A型机器人m台，购买总金额为w万元，请写出w与m的函数关系式；
②请你求出最节省的采购方案，购买总金额最低是多少万元？
23. (本小题10.0分)
如图，直线y=ax+b与双曲线y=kx交于点A(2,n)和点B(-4,-2)，过点A作AC⊥x轴，垂足为C．
(1)求直线y=ax+b和双曲线y=kx的解析式；
(2)连接BC，求△ABC的面积．

24. (本小题10.0分)
如图1是一台放置在水平桌面上的笔记本电脑，将其侧面抽象成如图2所示的几何图形，若显示屏所在面的侧边AO与键盘所在面的侧边BO长均为24cm，点P为眼睛所在位置，D为AO的中点，连接PD，当PD⊥AO时，称点P为“最佳视角点”，作PC⊥BC，垂足C在OB的延长线上，且BC=12cm．
(1)当PA=45cm时，求PC的长；
(2)若∠AOC=120°时，“最佳视角点”P在直线PC上的位置会发生什么变化？此时PC的长是多少？请通过计算说明．(结果精确到0.1cm，可用科学计算器，参考数据： 2≈1.414， 3≈1.732)


25. (本小题10.0分)
如图，Rt△ABC中∠ABC=90°，⊙O与△ABC的边AB、AC边分别相交于点E和点D(圆心O在AB上)，连接OD和BD，已知∠CBD=2∠A．
(1)求证：BD为⊙O的切线；
(2)若已知OD=1，DE=π3，求CD的长．

26. (本小题12.0分)
【阅读材料】
教材习题
如图，AB、CD相交于点O，O是AB中点，AC//BD，求证：O是CD中点．

问题分析
由条件易证△AOC≌△BOD，从而得到OC=OD，即点O是CD的中点
方法提取
构造“平行8字型”全等三角形模型是证明线段相等的一种常用方法
请运用上述阅读材料中获取的经验和方法解决下列问题．
【基础应用】已知△ABC中，∠B=90°，点E在边AB上，点F在边BC的延长线上，连接EF交AC于点D．
(1)如图1，若AB=BC，AE=CF，求证：点D是EF的中点；
(2)如图2，若AB=2BC，AE=2CF，探究CD与BE之间的数量关系；
【灵活应用】如图3，AB是半圆O的直径，点C是半圆上一点，点E是AB上一点，点F在BC延长线上，AB=8，AE=2，AECF=ABBC，当点C从点B运动到点A，点D运动的路径长为______ ，CF扫过的面积为______ ．


27. (本小题14.0分)
如图1，平面直角坐标系xOy中，抛物线y=ax2+bx+3(a<0)与x轴分别交于点A(-3,0)和点B(1,0)，与y轴交于点C，P为抛物线上一动点．
(1)写出抛物线的对称轴为直线______ ，抛物线的解析式为______ ；
(2)如图2，连结AC，若P在AC上方，作PQ//y轴交AC于Q，把上述抛物线沿射线PQ的方向向下平移，平移的距离为h(h>0)，在平移过程中，该抛物线与直线AC始终有交点，求h的最大值；
(3)若P在AC上方，设直线AP，BP与抛物线的对称轴分别相交于点F，E，请探索以A，F，B，G(G是点E关于x轴的对称点)为顶点的四边形面积是否随着P点的运动而发生变化，若不变，求出这个四边形的面积；若变化，说明理由．
(4)设M为抛物线对称轴上一动点，当P，M运动时，在坐标轴上是否存在点N，使四边形PMCN为矩形？若存在，直接写出点P的横坐标；若不存在，请说明理由．


答案和解析

1.【答案】A 
【解析】解：因为负数的绝对值等于它的相反数；
所以，-2023的绝对值等于2023．
故选：A．
利用绝对值的意义求解．
本题考查绝对值的含义，即：正数的绝对值是它本身，负数的绝对值是它的相反数．

2.【答案】A 
【解析】解：A．(-a)-1=-1a，故该选项错误，符合题意；
B.a3⋅a4=a7，故该选项正确，不符合题意；
C.(2a2)3=8a6，故该选项正确，不符合题意；
D.a3÷a2=a，故该选项正确，不符合题意；
故选：A．
根据负整数指数幂的运算，同底数幂的乘除法，积的乘方运算法则进行运算，即可一一判定．
本题考查了负整数指数幂的运算，同底数幂的乘除法，积的乘方运算，掌握和运用各运算法则是解决本题的关键．

3.【答案】A 
【解析】解：由题意得，这组数据的平均数是3+(-2)+4+(-3)+0+(-4)+27=0，-4<-3<-2<0<2<3<4．
∴这组数据的最大值是4，最小值是-4．
∴这组数据的极差是4-(-4)=8．
故选：A．
根据算术平均数的定义、极差的定义解决此题．
本题主要考查算术平均数、极差，熟练掌握算术平均数的定义、极差的定义是解决本题的关键．

4.【答案】B 
【解析】解：根据二次根式有意义的条件得：x+1≥0，
∴x≥-1，
根据分式有意义的条件得：x≠0，
∴自变量的取值范围为x≥-1且x≠0，
故选：B．
根据二次根式和分式有意义的条件，列出不等式求解即可．
本题考查了函数自变量的取值范围，掌握二次根式和分式有意义的条件是解题的关键．

5.【答案】C 
【解析】解：如图所示

主视图和左视图都是由4个正方形组成，俯视图由5个正方形组成，所以俯视图的面积最大．
故选：C．
从正面看，得到从左往右3列正方形的个数依次为1，2，1；从左面看，得到从左往右3列正方形的个数依次为1，2，1；从上面看得到从左往右3列正方形的个数依次为2，2，1，依此画出图形即可判断．

6.【答案】B 
【解析】解：∵EF是△ABC的中位线，AE=3，
∴EF//BC，BC=2EF，BE=AE=3，
∴∠EDB=∠DBC，
∵BD平分∠EBC，
∴∠EBD=∠DBC，
∴∠EDB=∠EBD，
∴ED=BE=3，
∵DF=1，
∴EF=ED+DF=3+1=4，
∴BC=8，
故选：B．
由三角形的中位线定理得到EF//BC，BC=2EF，BE=AE=3，利用等腰三角形的判定结合平行线的性质和角平分线的定义求出DE=3，可得EF=4，即可求出BC的长．
本题考查三角形的中位线定理，等腰三角形的判定，平行线的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．

7.【答案】D 
【解析】解：方法一：过点B作BH⊥AC于点H，如图所示：
则∠AHB=90°，
∵AD⊥BC，
∴∠ADB=∠ADC=90°，
∵BD=1，AD=4，
在Rt△ADB中，根据勾股定理得AB= 12+42= 17，
∵∠BAC=45°，
∴sin∠BAC=BHAB= 22，
∴BH= 342，
设CD=x，
则BC=1+x，
在Rt△ACD中，根据勾股定理得AC2=AD2+CD2=16+x2，
∵S△ABC=12AC⋅BH=12BC⋅AD，
∴AC2⋅BH2=BC2⋅AD2，
∴172(16+x2)=16(1+x)2，
解得x=-203(舍去)或x=2.4，
∴CD=2.4；
方法二：过点C作CE⊥AB于点E，如图所示：
则∠BEC=90°，
∵AD⊥BC，
∴∠ADB=90°，
∴∠ADB=∠BEC，
∵∠ABD=∠CBE，
∴△ABD∽△CBE，
∴CE：BE=AD：BD，
∵BD=1，AD=4，
∴CE：BE=4，
设BE=a，则CE=4a，
∵∠AEC=90°，∠BAC=45°，
∴∠ACE=45°，
∴AE=CE=4a，
∴AB=5a，
在Rt△ADB中，根据勾股定理得AB= 12+42= 17，
∴5a= 17，
∴a= 175，
∴BE= 175，CE=4 175，
在Rt△BCE中，根据勾股定理得BC= ( 175)2+(4 175)2=175，
∴CD=BC-BD=175-1=2.4，
故选：D．
方法一：过点B作BH⊥AC于点H，根据勾股定理可得AB的长，根据sin∠BAC=BHAB= 22，求出BH的长，设CD=x，根据S△ABC=12AC⋅BH=12BC⋅AD，进一步可得AC2⋅BH2=BC2⋅AD2，列方程求出x的值，即可确定CD的长度；
方法二：过点C作CE⊥AB于点E，可证△ABD∽△CBE，根据相似三角形的性质可得CE：BE=AD：BD=4，设BE=a，则CE=4a，可知AE=4a，根据AB= 17，求出a的值，可得BE和CE的长，在Rt△BEC中，根据勾股定理求出BC的长，再根据CD=BC-BD进一步计算即可．
本题考查了解直角三角形的应用，勾股定理，等积法，锐角三角函数，添加适当的辅助线构造直角三角形是解题的关键．

8.【答案】A 
【解析】解：连接OB，过C点作CM⊥OB于M点，过A点作AN⊥OB于N点，抛物线的对称轴与x轴交于点D，如图，

令y=0，得方程-49x2+83x=0，
解得：x1=0，x2=6，
∴A点坐标为(6,0)，即OA=6，
将y=-49x2+83x配成顶点式得：y=-49(x-3)2+4，
∴B点坐标为(3,4)，
∴BD=4，OD=3，
∵CM⊥OB，AN⊥OB，
∴∠BMC=∠ANO=90°，
根据抛物线对称轴的性质可知BD⊥OA，
∴∠BDO=90°，
在Rt△BDO中，
利用勾股定理得OB= OD2+BD2= 32+42=5，
∵∠OBD=∠CBM，∠BDO=∠BMC=90°，
∴△OBD∽△CBM，
同理可证得△OBD∽△OAN，
∴BCMC=BOOD，ANOA=BDOB，
∴BCMC=BOOD=53，即3BC=5MC，
∴3BC+5AC=5MC+5AC=5(AC+CM)，
∵当A、C、M三点共线，且三点连线垂直OB时，AC+CM最小，
∴AC+CM最小值为AN，如图所示，
∵ANOA=BDOB，
∴AN=BDOB×OA=45×6=245，
∴AC+CM最小值245，
∴即3BC+5AC=5(AC+CM)=24．
故选：A．
连接OB，过C点作CM⊥OB于M点，过A点作AN⊥OB于N点，抛物线的对称轴与x轴交于点D，先求出抛物线与坐标轴的交点坐标，继而得出BD、OA、OD，再证明△OBD∽△CBM，△OBD∽△OAN，进而可得3BC+5AC=5MC+5AC=5(AC+CM)，当A、C、M三点共线，且三点连线垂直OB时，AC+CM最小，根据ANOA=BDOB求出AN，AC+CM最小值即为AN，则问题得解．
本题考查了求抛物线与坐标轴的交点和抛物线顶点的坐标、相似三角形的判定与性质、垂线段最短等知识，利用三角形相似得出3BC=5MC，进而得出3BC+5AC=5(AC+CM)是解答本题的关键．

9.【答案】a(b+2)(b-2) 
【解析】
解：原式=a(b2-4)
=a(b+2)(b-2)，
故答案为：a(b+2)(b-2)
【分析】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
原式提取公因式，再利用平方差公式分解即可．  
10.【答案】1.4×10-5 
【解析】解：0.000014=1.4×10-5．
故答案为：1.4×10-5．
绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
本题考查用科学记数法表示较小的数，一般形式为a×10-n，其中1≤|a|<10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．

11.【答案】5 
【解析】解：扇形的弧长=150π×12180=10π，
设圆锥的底面半径为R，则2πR=10π，
所以R=5．
故答案为：5；
根据弧长公式先计算出扇形的弧长，再利用圆的周长和圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长求解．
本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．

12.【答案】x=-4 
【解析】解：设这个一元二次方程的另一根为x2，
∵关于x的方程x2+mx-4=0的一根为x=1，
∴1×x2=-41
∴x2=-4
故答案为：x=-4．
设这个一元二次方程的另一根为x2，根据一元二次方程的根与系数的关系可得结果．
本题主要考查了一元二次方程根与系数的关系，熟练掌握一元二次方程根与系数的关系是解本题的关键．

13.【答案】3 3 
【解析】解：如图，在优弧AC上取一定D，连接AD、CD，连接AC，过点O作OM⊥AC于点M，

∵四边形内接于⊙O，∠AOC=2∠ADC，
∴∠ADC+∠ABC=12∠AOC+∠ABC=180°．
又∠AOC=∠ABC，
∴∠AOC=120°，
∵OA=OC，
∴∠OAM=∠OCM=30°，
∵OM⊥AC，
∴AC=2AM，
在Rt△OAM中，cos∠OAM=cos30°=AMOA= 32，
∵OA=3，
∴AM=32 3，
∴AC=3 3，
故答案为：3 3．
在优弧AC上取一定D，连接AD、CD，连接AC，过点O作OM⊥AC于点M，利用圆周角定理和圆内接四边形的性质及垂径定理求得∠AOC=∠ABC=120°，AC=2AM，，解直角三角形进行解答即可．
此题考查了圆周角定理、垂径定理，熟记圆周角定理、垂径定理是解题的关键．

14.【答案】-1 【解析】解：∵反比例函数y=k2x(k≠0)中的k2>0，
∴反比例函数y=k2x(k≠0)的图象经过第一、三象限，且在每一象限内y随x的增大而减小．
∵y2>y1，a+1>a，
∴点A位于第三象限，点B位于第一象限，
∴a<0a+1>0，
解得-1 故答案是：-1 根据反比例函数图象所经过的象限和函数的增减性解答．
考查了反比例函数图象上点的坐标特征，解题时，需要熟悉反比例函数解析式中系数与图象的关系．

15.【答案】8π-8 3 
【解析】解：连接OO'，AO'，AB，A'B，如图所示：

根据旋转可知，∠OBO'=∠ABA'=60°，
∵OB=OO'，
∴△OBO'为等边三角形，
∴∠BOO'=60°，BO'=BO，
∵∠AOB=120°，
∴∠AOO'=60°，
∵AO=OO'，
∴△AOO'为等边三角形，
∴AO'=AO，∠AOO'=∠BOO'=60°，
∴OA=OB=BO'=AO'，
∴四边形AOBO'为菱形，
∴S弓形AO'=S弓形BO'，
记菱形的对角线的交点为H，且OB=OA=AO'=BO'=OO'=4，
∴OH=O'H=2,BH=AH= 42-22=2 3，
∴S菱形AOBO'=12×4×4 3=8 3，
∵四边形AOBO'为菱形，∠OBO'=∠ABA'=60°，
∴∠ABO'=30°=∠A'BO'，
∵AB=A'B，BO'=BO'，
∴△ABO'≌△A'BO'，
∴S△ABO'+S△A'BO'=S菱形AOBO'=8 3，
∵S扇形BAA'=60π×(4 3)2360=8π，
∴S阴影=S扇形-S菱形=8π-8 3．
故答案为：8π-8 3．
连接OO'，AO'，AB，A'B，根据旋转，结合等边三角形的判定，得出△OBO'为等边三角形，得出∠BOO'=60°，BO'=BO，再证明△AOO'为等边三角形，从而证明四边形AOBO'为菱形，证明S阴影=S扇形-S菱形，从而可得答案．
本题主要考查了扇形的面积公式，等边三角形的判定和性质，菱形的判定和性质，熟练掌握扇形面积公式，看出图中S阴影=S扇形-S菱形是解本题的关键．

16.【答案】16 1015 
【解析】解：作AM⊥BC于M，
∵AB=AC=5，BC=8，
∴BM=CM=4，
∴AM= AB2-AM2=3，
∵BD=AB=5，
∴DM=5-4=1，
∴AD= 32+12= 10，CD=4-1=3，
∵AB=AC，
∴∠B=∠C，
∵∠ADE=∠B，
∴∠ADE=∠C，
∵BD=AB，
∴∠BAD=∠BDA，
∵∠BAD=∠ADE+∠E，∠BDA=∠C+∠DAC，
∴∠E=∠DAC，
∴△ADE∽△DCA，
∴DEAC=ADCD，即DE5= 103，
∴DE=5 103，
∵∠ADE=∠C，∠DAF=∠CAD，
∴△ADF∽△ACD，
∴DFCD=ADAC，即DF3= 105，
∴DF=3 105，
∴EF=DE-DF=5 103-3 105=16 1015．
故答案为：16 1015．
作AM⊥BC于M，根据等腰三角形的性质以及等腰三角形三线合一的性质得出DM=1，CD=3，利用勾股定理求得AD= 10，通过证得△ADE∽△DCA，求得DE=5 103，通过证得△ADF∽△ACD，求得DF=3 105，从而求得EF=DE-DF=16 1015．
本题考查了等腰三角形的性质，勾股定理的应用，三角形相似的判定和性质，正确应用性质定理是解题的关键．

17.【答案】解：(-1)2023+| 2-2|-2cos45°+ 8
=-1+2- 2-2× 22+2 2
=-1+2- 2- 2+2 2
=1． 
【解析】先计算特殊角的三角函数值、绝对值、乘方和二次根式，再计算乘法，后计算加减．
此题考查了实数的混合运算能力，关键是能确定准确的运算顺序，并能对各种运算进行准确计算．

18.【答案】解：x+2≥2x-13x+12-1>x-2，
解得x≤3x>-3．
∴-3 则符合条件的整数解为：-2，-1，0，1，2，3． 
【解析】根据解不等式组的基本步骤解答即可．
本题考查了解不等式组及其整数解，正确解不等式组是解题的关键．

19.【答案】解：(1-1x-1)÷x-2x2-1
=x-1-1x-1⋅(x+1)(x-1)x-2
=x-2x-1⋅(x+1)(x-1)x-2
=x+1，
∵x是方程x2-2x-3=0的根，
∴x1=3，x2=-1，
∵x=-1时，原分式无意义，
∴x=3，
∴当x=3时，原式=3+1=4． 
【解析】先根据分式混合运算的法则把原式进行化简，再根据x是方程x2-2x-3=0的根求出x的值，把x的值代入进行计算即可．
本题考查分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

20.【答案】50  10  72 
【解析】解：(1)m=15÷30%=50，
n%=5÷50×100%=10%，
故答案为：50，10；
(2)硬件专业的毕业生有：50×40%=20(人)，
补全的条形统计图如图所示；

在扇形统计图中，“软件”所对应的扇形的圆心角是360°×1050=72°；
故答案为：72；
(3)600×30%=180(名)，
答：估计“总线”专业的毕业生有180名．
(1)根据总线的人数和所占的百分比，可以求得m的值，然后即可计算出n的值；
(2)根据(1)中的结果和硬件所占的百分比，可以求得硬件专业的毕业生，从而可以将条形统计图补充完整；根据条形统计图中的数据，可以计算出在扇形统计图中，“软件”所对应的扇形的圆心角的度数；
(3)根据统计图中的数据，可以计算出“总线”专业的毕业生的人数．
本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．

21.【答案】解：(1)他从中随机抽取一个比赛项目，恰好抽中“论语”的概率=14．
(2)画树状图为：

共有12种等可能的结果数；
其中恰好小明抽中“唐诗”且小红抽中“宋词”的结果数为1，小明和小红都没有抽到“三字经”的结果数为6；
所以恰好小明抽中“唐诗”且小红抽中“宋词”的概率=112；
小明和小红都没有抽到“三字经”的概率=612=12． 
【解析】(1)直接利用概率公式求解；
(2)先画树状图展示所有12种等可能的结果数，再找出恰好小红抽中“唐诗”且小明抽中“宋词”和小明和小红都没有抽到“三字经”的结果数，然后根据概率公式求解．
本题考查了列表法与树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或事件B的概率．

22.【答案】解：(1)设每台A型机器人每天搬运货物x吨，则每台B型机器人每天搬运货物(x+10)吨，
由题意得：540x=600x+10，
解得：x=90，
当x=90时，x(x+10)≠0，
∴x=90是分式方程的根，
∴x+10=90+10=100(吨)，
答：每台A型机器人每天搬运货物90吨，则每台B型机器人每天搬运货物100吨；
(2)①由题意得：w=1.2m+2(30-m)=-0.8m+60；
②由题意得：90m+100(30-m)≥28201.2m+3(30-m)≤48，
解得：15≤m≤18，
∵-0.8<0，
∴w随m的增大而减小，
∴当m=18时，w最小，此时w=-0.8×18+60=45.6，
∴购买A型机器人18台，B型机器人12台时，购买总金额最低是45.6万元． 
【解析】(1)设每台A型机器人每天搬运货物x吨，则每台B型机器人每天搬运货物(x+10)吨，根据题意列出分式方程，解方程检验后即可得出答案；
(2)①根据题意列出一次函数解析式即可；
②先根据题意列出一元一次不等式组，解不等式组求出m的取值范围，再根据一次函数的性质，即可求出答案．
本题考查了一次函数的应用，一元一次不等式组的应用，根据题意找出题目中的相等关系，不等关系列出分式方程，一元一次不等式组及列出一次函数关系式是解决问题的关键．

23.【答案】解：(1)把点B(-4,-2)代入y=kx得：-2=k-4，即k=8，
∴双曲线的解析式为y=8x；
把点A(2,n)代入y=8x得，n=4，
∴A(2,4)，
把A，B代入y=ax+b得：
2a+b=4 -4a+b=-2 ，
解得：a=1 b=2 ，
∴直线的解析式为y=x+2；
(2)过点B作BD⊥y轴，交AC延长线于D，

∵A(2,4)，AC⊥x轴，垂足为C，
∴点C的坐标为(2,0)，
∴AC=4．
∵B(-4,-2)，
∴D(2,-2)，
∴BD=6，
∴△ABC的面积=12×AC×BD=12×4×6=12． 
【解析】(1)把点B(-4,-2)代入y=kx，可得双曲线的解析式为y=8x，再求出A(2,4)，再把A，B代入y=ax+b，即可求解；
(2)过点B作BD⊥y轴，交AC延长线于D，可得AC=4，BD=6，再根据三角形的面积公式计算，即可求解．
本题考查了反比例函数与一次函数的交点问题，考查了待定系数法求函数的解析式，反比例函数图象上点的坐标特征，三角形的面积，求得交点坐标是解题的关键．

24.【答案】解：(1)当PA=45cm时，连结PO．
∵D为AO的中点，PD⊥AO，
∴PO=PA=45cm．
∵BO=24cm，BC=12cm，∠C=90°，
∴OC=OB+BC=36cm，PC= 452-362=27cm；

(2)当∠AOC=120°，过D作DE⊥OC交BO延长线于E，过D作DF⊥PC于F，则四边形DECF是矩形．
在Rt△DOE中，∵∠DOE=60°，DO=12AO=12，
∴DE=DO⋅sin60°=6 3，EO=12DO=6，
∴FC=DE=6 3，DF=EC=EO+OB+BC=6+24+12=42．
在Rt△PDF中，∵∠PDF=30°，
∴PF=DF⋅tan30°=42× 33=14 3，
∴PC=PF+FC=14 3+6 3=20 3≈34.68>27，
∴点P在直线PC上的位置上升了． 
【解析】(1)连结PO.先由线段垂直平分线的性质得出PO=PA=45cm，则OC=OB+BC=36cm，然后利用勾股定理即可求出PC= 452-362=27cm；
(2)过D作DE⊥OC交BO延长线于E，过D作DF⊥PC于F，则四边形DECF是矩形．先解Rt△DOE，求出DE=DO⋅sin60°=6 3，EO=12DO=6，则FC=DE=6 3，DF=EC=EO+OB+BC=42.再解Rt△PDF，求出PF=DF⋅tan30°=42× 33=14 3，则PC=PF+FC=14 3+6 3=20 3≈34.68>27，即可得出结论．
本题考查了解直角三角形的应用，线段垂直平分线的性质，勾股定理，矩形的判定与性质，锐角三角函数的定义，准确作出辅助线构造直角三角形是解题的关键．

25.【答案】(1)证明：∵∠DOB=2∠A，∠CBD=2∠A，
∴∠CBD=∠DOB，
∵∠ABC=90°，
∴∠ABD+∠CBD=90°，
∴∠DOB+∠DBO=90°，
∴∠ODB=180°-(∠DOB+∠BDO)=90°，
即：OD⊥BD，
∵OD为半径，
∴BD与⊙O相切；
(2)解：设∠DOE=n°，
∵DE=π3，OD=1，
∴nπ×1180=π3，
解得：n=60，
∴∠DOE=60°，
∴∠DBC=∠DOE=60°．
∵∠A=12∠DOE，
∴∠A=30°．
∵OA=OD，
∴∠ODA=∠A=30°，
∴∠CDB=180°-∠ODA-∠ODB=180°-30°-90°=60°，
∴△CDB为等边三角形，
∴CD=DB．
在Rt△ODB中，
∵tan∠DOB=BDOD，
∴BD=OD⋅tan60°=1× 3= 3，
∴CD=BD= 3． 
【解析】(1)根据等腰三角形的性质得到∠A=∠ODA，根据三角形外角的性质得到∠DOB=2∠A，推出∠CBD=∠DOB，根据∠ABC=90°即可证得∠ODB=90°，则可得BD为⊙O的切线；
(2)根据弧长公式求出∠DOE=60°，根据含30°角的直角三角形三边关系，得到BD= 3，推出∠C=∠CBD，即可求出CD的长．
本题考查了切线的判定、等腰三角形的性质、三角形外角的性质、弧长公式、含30°角的直角三角形的三边关系等知识点；弧长公式：l=nπr180要牢记，切线的判定分知道切点和不知道切点，知道切点：连半径，证垂直；不知道切点：作垂直，证半径．牢记知识点是解答本题的关键．

26.【答案】52π 92π 
【解析】(1)证明：∵AB=BC，∠B=90°，
∴∠A=∠ACB=45°，
过点E作EG//BF，则∠AGE=∠ACB=45°，∠AEG=∠B=90°，

∴△AEG是等腰直角三角形，则AE=GE，
∵AE=CF，
∴GE=CF，
∵∠AGE=∠ACB=45°，
∴∠DGE=∠DCF=135°，
又∵∠GDE=∠CDF，
∴△DGE≌△DCF，
∴DE=DF，
∴点D是EF的中点；

(2)过点E作EG//BF，则△AEG∽△ABC，

∴AEEG=ABBC，
∵AB=2BC，AE=2CF，则AE=2EG，
∴EG=CF，
∵EG//BF，
∴∠AGE=∠ACB，∠AEG=∠B=90°，
∴∠DGE=∠DCF，
又∵∠GDE=∠CDF，
∴△DGE≌△DCF(AAS)，
∴CD=DG，
∵EG//BF，
∴AGAE=GCBE=2CDBE，
∵AE=2EG，则AG= AE2+EG2= 5EG
∴AGAE= 52，
∴AGAE=2CDBE= 52，
∴CD= 54BE；
灵活应用：
∵AB是半圆O的直径，点C是半圆上一点，
∴∠ACB=90°，
过点E作EG//BF，则△AEG∽△ABC，

∴AEEG=ABBC，
∵AECF=ABBC，
∴EG=CF，
∵EG//BF，
∴∠AGE=∠ACB=90°，
∴∠DGE=∠DCF=90°，
又∵∠GDE=∠CDF，
∴△DGE≌△DCF(AAS)，
∴CD=DG，
过点D作DM//BF，则DGEM=CDBM，∠ADM=90°，
∴EM=BM，
∵AB=8，AE=2，
∴BE=6，则EM=BM=12BE=3，
∴AM=AE+EM=5，
∴点D在以AM为直径的半圆上运动，
∴D运动的路径长为：12AM⋅π=52π，
过点F作FH//AC，则ABBC=AHCF，∠BFH=90°，
∵AECF=ABBC，
∴AE=AH=2，
∴BH=AH+AB=10，
∴点F在以BH为直径的半圆上运动，
则CF扫过的面积为以BH为直径的半圆与以AB为直径的半圆的面积之差，
即：CF扫过的面积为12(BH2)2π-12(AB2)2π=92π，
故答案为：52π，92π．
(1)过点E作EG//BF，证△DGE≌△DCF，即可得点D是EF的中点；
(2)过点E作EG//BF，可证△AEG∽△ABC，得AEEG=ABBC，由AB=2BC，AE=2CF，得EG=CF，再证△DGE≌△DCF，可得CD=DG，由平行线分线段成比例得AGAE=GCBE=2CDBE，由AE=2EG，可得AG= AE2+EG2= 5EG，AGAE= 52即可得CD= 54BE；
灵活应用：由题意可得∠ACB=90°，过点E作EG//BF，则△AEG∽△ABC，可得AEEG=ABBC，进而可得EG=CF，易证△DGE≌△DCF，可知CD=DG，过点D作DM//BF，则DGEM=CDBM，∠ADM=90°，易知点D在以AM为直径的半圆上运动，可求得D运动的路径长度，过点F作FH//AC，则ABBC=AHCF，∠BFH=90°，易知点F在以BH为直径的半圆上运动，可知CF扫过的面积为以BH为直径的半圆与以AB为直径的半圆的面积之差，即可求得答案．
本题考查全等三角形的判定及性质，相似三角形的判定及性质，平行线分线段成比例，圆周角定理，动点的运动路径，添加辅助线构造全等三角形是解决问题的关键．

27.【答案】x=-1  y=-x2-2x+3 
【解析】解：(1)由题意得，抛物线的表达式为：y=a(x+3)(x-1)=a(x2+2x-3)，
则-3a=3，则a=-1，
故抛物线的表达式为：y=-x2-2x+3，
则抛物线的对称轴为x=-1，
故答案为：x=-1，y=-x2-2x+3；

(2)由题意得，平移后的抛物线表达式为：y=-x2-2x+3-h①，
由抛物线的表达式知，点C(0,3)，
由点A、C的坐标得，直线AC的表达式为：y=x+3②，
联立①②得：-x2-2x+3-h=x+3，
则Δ=9-4h=0，
则h=94，
即h的最大值为：94；

(3)面积不变，为8，理由：
设点P的坐标为(m,-m2-2m+3)，

由点A、P的坐标得，直线AP的表达式为：y=(1-m)(x+3)，
当x=-1时，y=(1-m)(x+3)=2-2m，
即点F(-1,2-2m)，
同理可得，点E(-1,2m+6)，则点G(-1,-2m-6)，
则FG=2-2m+2m+6=8，
则S四边形AGBF=12×AB×FG=12×4×8=16，
即以A，F，B，G(G是点E关于x轴的对称点)为顶点的四边形面积不随着P点的运动而发生变化，这个四边形的面积为16；

(4)存在，理由如下：
如下图，当点N在y轴上时，四边形PMCN是矩形，此时P(-1,4)，N(0,4)；

如图，当四边形PMCN是矩形时，设M(-1,n)，P(t,-t2-2t+3)，则N(t+1,0)，

由题意n-(-t2-2t+3)=313-n=3t+1，
消去n得，3t2+5t-10=0，
解得t=-5± 1456，
综上所述，满足条件的点P的横坐标为：-5± 1456，-1．
(1)用待定系数法即可求解；
(2)平移后的抛物线表达式为：y=-x2-2x+3-h①由Δ=9-4h=0，即可求解；
(3)求出点F(-1,2-2m)，点G(-1,-2m-6)，则FG=2-2m+2m+6=8，即可求解；
(4)当点N在y轴上时，四边形PMCN是矩形，此时P(-1,4)，N(0,4)；当四边形PMCN是矩形时，设M(-1,n)，P(t,-t2-2t+3)，则N(t+1,0)，由题意n-(-t2-2t+3)=313-n=3t+1，即可求解．
本题属于二次函数综合题，考查了二次函数的性质，矩形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会利用参数构建方程解决问题，属于中考压轴题．