



所属成套资源:2023-2024学年升初三(新九年级)数学暑假衔接教材(人教版)
2.2-y=ax2+k-2023年升初三人教版暑假衔接教材
展开这是一份2.2-y=ax2+k-2023年升初三人教版暑假衔接教材,文件包含22-yax2+k解析版-2023年升初三人教版暑假衔接教材docx、22-yax2+k原卷版-2023年升初三人教版暑假衔接教材docx等2份试卷配套教学资源,其中试卷共17页, 欢迎下载使用。
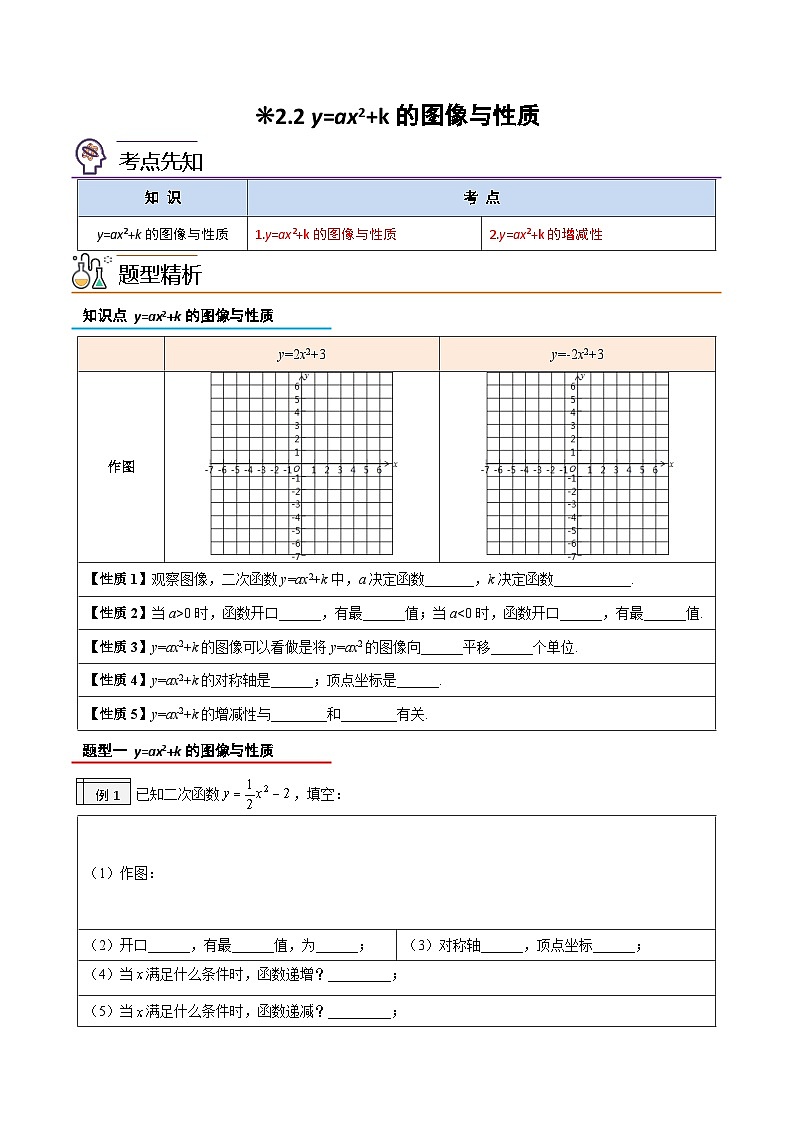
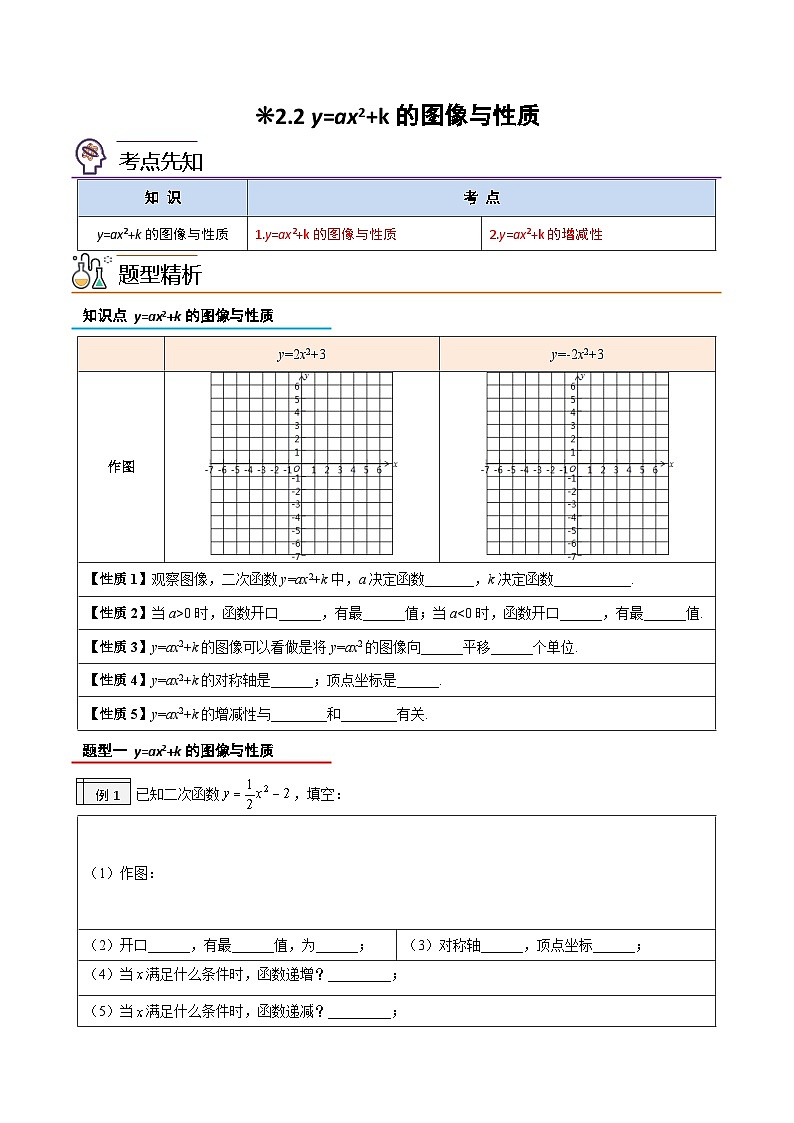
❊2.2 y=ax2+k的图像与性质
知 识 | 考 点 | |
y=ax2+k的图像与性质 | 1.y=ax2+k的图像与性质 | 2.y=ax2+k的增减性 |
| y=2x2+3 | y=-2x2+3 |
作图 | ||
【性质1】观察图像,二次函数y=ax2+k中,a决定函数_______,k决定函数___________. | ||
【性质2】当a>0时,函数开口______,有最______值;当a<0时,函数开口______,有最______值. | ||
【性质3】y=ax2+k的图像可以看做是将y=ax2的图像向______平移______个单位. | ||
【性质4】y=ax2+k的对称轴是______;顶点坐标是______. | ||
【性质5】y=ax2+k的增减性与________和________有关. | ||
已知二次函数,填空:
(1)作图: | |
(2)开口______,有最______值,为______; | (3)对称轴______,顶点坐标______; |
(4)当满足什么条件时,函数递增?_________; | |
(5)当满足什么条件时,函数递减?_________; | |
(6)函数图像是否过点与?______,我们能够发现什么规律?_____________________. | |
(7)函数离对称轴越远,函数值越______. | |
已知二次函数,填空:
(1)作图: | |
(2)开口______,有最______值,为______; | (3)对称轴______,顶点坐标______; |
(4)当满足什么条件时,函数递增?_________; | |
(5)当满足什么条件时,函数递减?_________; | |
(6)函数图像是否过点与?______,我们能够发现什么规律?___________________. | |
(7)函数离对称轴越远,函数值越______. | |
关于抛物线下列说法正确的是( )
A.开口向上 | B.对称轴是y轴 |
C.有最小值 | D.当时,函数y随x的增大而减小 |
抛物线 的开口______,对称轴是______,顶点坐标是______,当______时,随的增大而增大,当x______时,随的增大而减小.
抛物线与抛物线的相同点是( )
A.顶点相同 | B.对称轴不相同 |
C.开口方向一样 | D.顶点都在y轴上 |
抛物线,,共有的性质是( )
A.开口向上 | B.对称轴都是y轴 |
C.都有最高点 | D.顶点都是原点 |
抛物线在y轴的左侧部分,y的值随着x的值增大而_______.(填“增大”或“减小”)
抛物线在轴的右侧呈_______趋势(填“上升”或者“下降”).
抛物线的顶点坐标为_______.
抛物线的顶点坐标是_______.
已知点,,在二次函数的图象上,则,,的大小关系是_______.
【分析】函数的开口方向向______,对称轴是______,所以离对称轴越远函数值越______. 【解答】在-3、-2和1中,它们距离非常轴的距离分别是_____、_____、_____,所以大小关系是__________. |
已知在二次函数的图象上,则为的大小关系正确的是( )
A. | B. | C. | D. |
已知,点,,都在函数的图象上,则( )
A. | B. | C. | D. |
已知,,是抛物线(k为常数)上的点,则_______.
【分析】函数的开口方向向______,对称轴是______,所以离对称轴越远函数值越______. 【解答】在-3、-2和1中,它们距离非常轴的距离分别是_____、_____、_____,所以大小关系是__________. |
已知点,点在抛物线上,且,且的取值范围是( )
A. | B. | C. | D. |
已知点,,三点都在抛物线的图象上,则的大小关系是( )
A. | B. | C. | D. |
对于二次函数,当时,的取值范围是________.
【分析】函数的开口方向向______,对称轴是______,所以离对称轴越远函数值越______. 【解答】-2和4谁离对称轴更远?______,所以当x=______时取最______值,为______;当x=______时取最______值,为______. |
对于二次函数,当时,的取值范围是________.
【分析】函数的开口方向向______,对称轴是______,所以离对称轴越远函数值越______. 【解答】-1和2谁离对称轴更远?______,所以当x=______时取最______值,为______;当x=______时取最______值,为______. |
1.对于二次函数,下列说法中不正确的是( )
A.图象的开口向上 | B.函数的最小值为1 |
C.图象的对称轴为直线 | D.当时随的增大而减小 |
2.抛物线的顶点坐标是( )
A. | B. | C. | D. |
3.抛物线的对称轴是( )
A.直线 | B.直线 | C.直线 | D.直线 |
4.已知抛物线有最低点,那么的取值范围是( )
A. | B. | C. | D. |
5.抛物线( )
A.开口向上,且有最高点 | B.开口向上,且有最低点 |
C.开口向下,且有最高点 | D.开口向下,且有最低点 |
6.当时,二次函数的图象大致是( )
A. | B. | C. | D. |
7.设点,,是抛物线上的三点,则,,的大小关系为( )
A. | B. | C. | D. |
8.已知抛物线过,,三点,则,,大小关系是( )
A. | B. | C. | D. |
9.对于二次函数,当时,
(1)函数的开口方向是_______;对称轴是_______;顶点坐标是_______;
(2)离对称轴越远,函数值越______;
(3)当______,函数的最大值为______;当______,函数的最小值为______.
相关试卷
这是一份2.10-二次函数的实际应用-2023年升初三人教版暑假衔接教材,文件包含210-二次函数的实际应用解析版-2023年升初三人教版暑假衔接教材docx、210-二次函数的实际应用原卷版-2023年升初三人教版暑假衔接教材docx等2份试卷配套教学资源,其中试卷共73页, 欢迎下载使用。
这是一份2.9-二次函数的实际应用-2023年升初三人教版暑假衔接教材,文件包含29-二次函数的实际应用解析版-2023年升初三人教版暑假衔接教材docx、29-二次函数的实际应用原卷版-2023年升初三人教版暑假衔接教材docx等2份试卷配套教学资源,其中试卷共62页, 欢迎下载使用。
这是一份2.4-y=ax2+bx+c-2023年升初三人教版暑假衔接教材,文件包含24-yax2+bx+c解析版-2023年升初三人教版暑假衔接教材docx、24-yax2+bx+c原卷版-2023年升初三人教版暑假衔接教材docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。












