中考数学思维训练专题二

 归纳猜想

归纳猜想型问题对考生的观察分析能力要求较高，经常以填空等形式出现，解题时要善于从所提供的数字或图形信息中，寻找其共同之处，这个存在于个例中的共性，就是规律。其中蕴含着“特殊——一般——特殊”的常用模式，体现了总结归纳的数学思想，这也正是人类认识新生事物的一般过程。相对而言，猜想结论型问题的难度较大些，具体题目往往是直观猜想与科学论证、具体应用的结合，解题的方法也更为灵活多样：计算、验证、类比、比较、测量、绘图、移动等等，都能用到。

由于猜想本身就是一种重要的数学方法，也是人们探索发现新知的重要手段，非常有利于培养创造性思维能力，所以备受命题专家的青睐，逐步成为中考的持续热点。

猜想数式规律

观察下面的单项式：a，2a2，4a3，8a4，…，根据你发现的规律，第8个式子是　   　．

有这样一组数据a1，a2，a3，…an，满足以下规律：a1＝，a2＝，a3＝，…an＝（n≥2且a为正整数），则a2018＝　   　．

已知

…

依据上述规律

计算的结果为　   　（写成一个分数的形式）

对于任意非零实数a、b，定义运算“⊕”，使下列式子成立：1⊕2＝﹣，2⊕1＝，（﹣2）⊕5＝，5⊕（﹣2）＝﹣，…，则a⊕b＝　   　．

猜想图形规律

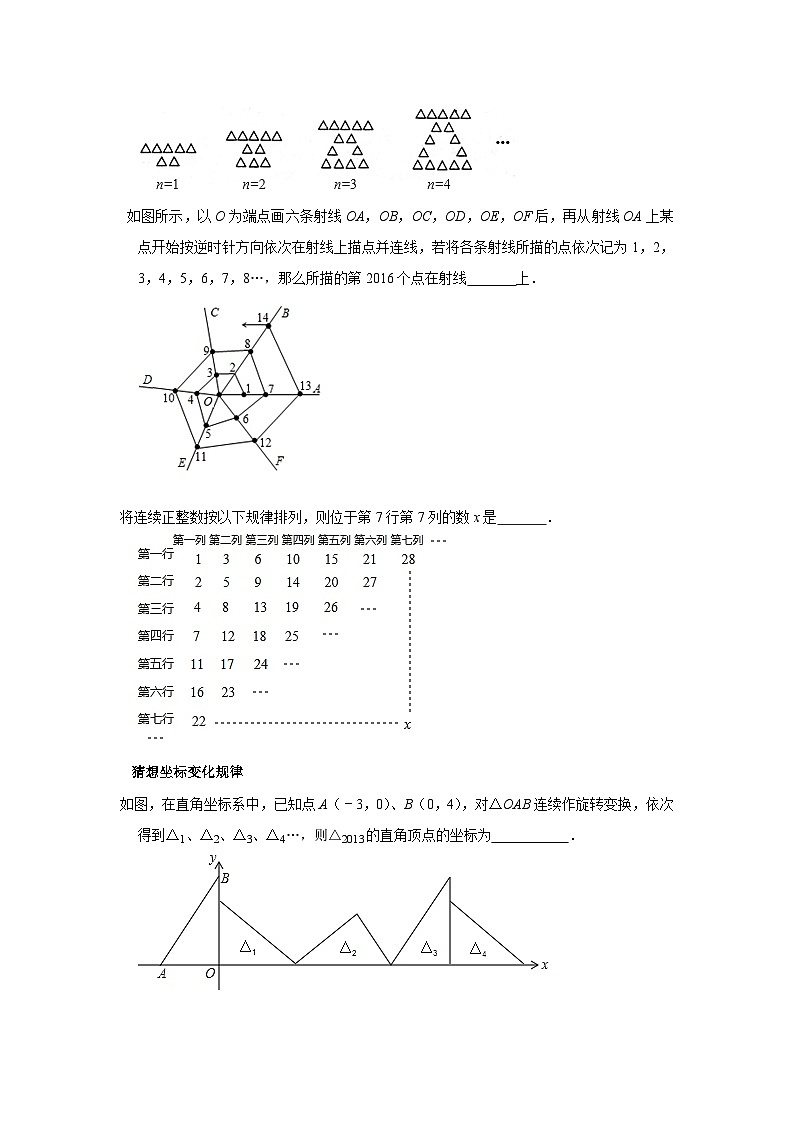
用大小相同的小三角形摆成如图所示的图案，按照这样的规律摆放，则第n个图案中共有小三角形的个数是　  　．

 如图所示，以O为端点画六条射线OA，OB，OC，OD，OE，OF后，再从射线OA上某点开始按逆时针方向依次在射线上描点并连线，若将各条射线所描的点依次记为1，2，3，4，5，6，7，8…，那么所描的第2016个点在射线　   　上．

将连续正整数按以下规律排列，则位于第7行第7列的数x是　   　．

猜想坐标变化规律

如图，在直角坐标系中，已知点A（﹣3，0）、B（0，4），对△OAB连续作旋转变换，依次得到△1、△2、△3、△4…，则△2013的直角顶点的坐标为　       　．

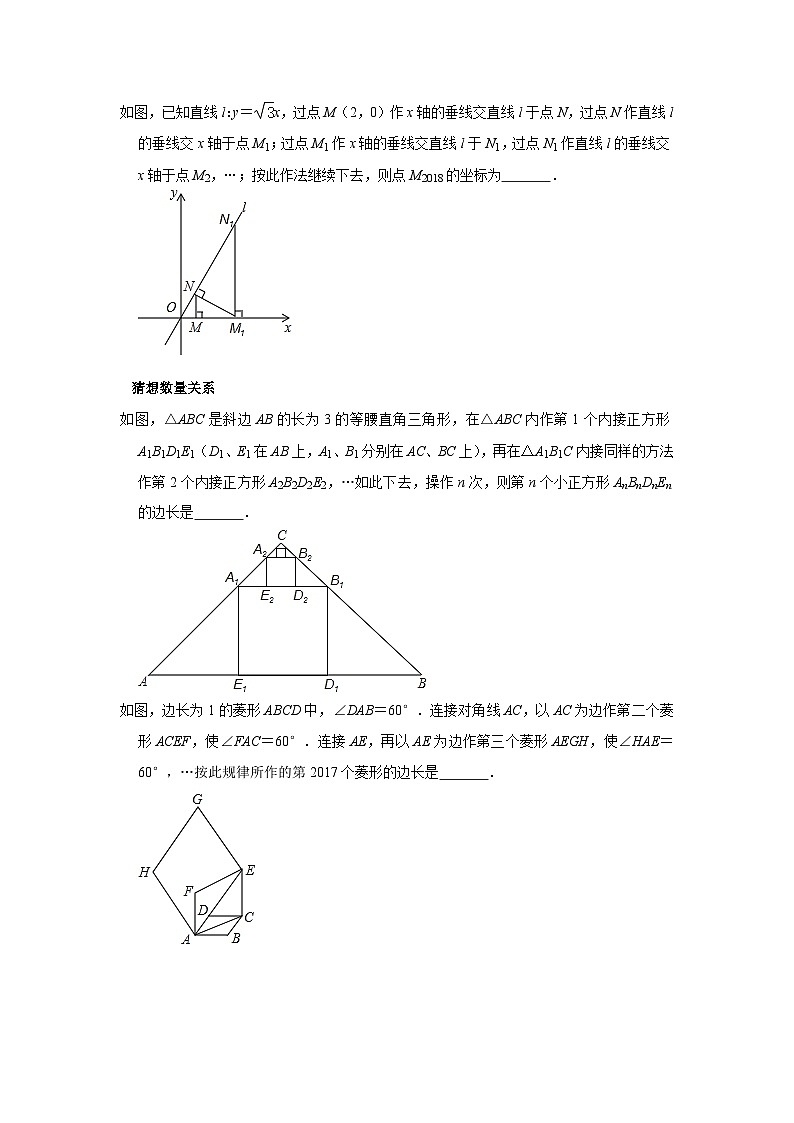
如图，已知直线l：y＝x，过点M（2，0）作x轴的垂线交直线l于点N，过点N作直线l的垂线交x轴于点M1；过点M1作x轴的垂线交直线l于N1，过点N1作直线l的垂线交x轴于点M2，…；按此作法继续下去，则点M2018的坐标为　   　．

猜想数量关系

如图，△ABC是斜边AB的长为3的等腰直角三角形，在△ABC内作第1个内接正方形A1B1D1E1（D1、E1在AB上，A1、B1分别在AC、BC上），再在△A1B1C内接同样的方法作第2个内接正方形A2B2D2E2，…如此下去，操作n次，则第n个小正方形AnBnDnEn的边长是　   　．

如图，边长为1的菱形ABCD中，∠DAB＝60°．连接对角线AC，以AC为边作第二个菱形ACEF，使∠FAC＝60°．连接AE，再以AE为边作第三个菱形AEGH，使∠HAE＝60°，…按此规律所作的第2017个菱形的边长是　   　．

正方形ABCD的顶点A在直线MN上，点O是对角线AC、BD的交点，过点O作OE⊥MN于点E，过点B作BF⊥MN于点F．

（1）如图1，当O、B两点均在直线MN上方时，求证：AF＝AE+OE；

（2）当正方形ABCD绕点A顺时针旋转至图2的位置时，线段AF、AE、OE之间又有怎样的数量关系？

如图1，等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合，将此三角板绕点A旋转，使三角板中该锐角的两条边分别交正方形的两边BC，DC于点E，F，连接EF．

（1）猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；

（2）在图1中，过点A作AM⊥EF于点M，请直接写出AM和AB的数量关系；

（3）如图2，将Rt△ABC沿斜边AC翻折得到Rt△ADC，E，F分别是BC，CD边上的点，∠EAF＝∠BAD，连接EF，过点A作AM⊥EF于点M，试猜想AM与AB之间的数量关系．并证明你的猜想．

猜想变化情况

如图，OP＝1，过P作PP1⊥OP，得OP1＝；再过P1作P1P2⊥OP1且P1P2＝1，得OP2＝；又过P2作P2P3⊥OP2且P2P3＝1，得OP3＝2；…依此法继续作下去，若△OPnPn+1的面积大于6时，n至少是　   　．

已知等边三角形ABC的边长是2，以BC边上的高AB1为边作等边三角形，得到第一个等边三角形AB1C1，再以等边三角形AB1C1的B1C1边上的高AB2为边作等边三角形，得到第二个等边三角形AB2C2，再以等边三角形AB2C2的边B2C2边上的高AB3为边作等边三角形，得到第三个等边△AB3C3；…，如此下去，这样得到的第n个等边三角形ABn∁n的面积为　        　．

如图，正方形ABCD的边长为3，点E，F分别在边AB，BC上，AE＝BF＝1，小球P从点E出发沿直线向点F运动，每当碰到正方形的边时反弹，反弹时反射角等于入射角．当小球P第一次碰到BC边时，小球P所经过的路程为　   　；当小球P第一次碰到AD边时，小球P所经过的路程为　   　；当小球P第n（n为正整数）次碰到点F时，小球P所经过的路程为　   　．

把边长为1的正方形纸片OABC放在直线m上，OA边在直线m上，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时，点O运动到了点O1处（即点B处），点C运动到了点C1处，点B运动到了点B1处，又将正方形纸片AO1C1B1绕B1点，按顺时针方向旋转90°…，按上述方法经过61次旋转后，顶点O经过的总路程为　   　．

如图，矩形ABCD中，AB＝6，第1次平移将矩形ABCD沿AB的方向向右平移5个单位，得到矩形A1B1C1D1，第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位，得到矩形A2B2C2D2…，第n次平移将矩形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位，得到矩形AnBn∁nDn（n＞2）．

（1）求AB1和AB2的长．

（2）若ABn的长为56，求n．

我们把正六边形对角线的交点称为它的中心，正六边形的顶点及它的中心称作特征点，如图（1）有六个顶点和一个中心点，因此共有7个特征点，照图（1）的方式继续排列正六边形，使得相邻两个正六边形的一边重合，这样得到图（2），图（3）…

观察以上图形得到表：

（1）第n个图形的特征点有多少个？

（2）第100个图形的特征点有多少个？

（3）第几个图形有2017个特征点？请说明理由．