北师大版八年级下册4 多边形的内角与外角和备课课件ppt

这是一份北师大版八年级下册4 多边形的内角与外角和备课课件ppt，共36页。PPT课件主要包含了第六章平行四边形，情景引入，都是360°，猜想与证明，典例精析，运用了整体思想，···，n-3，n-2，······等内容，欢迎下载使用。
6.4 多边形的内角和与外角和
法国的建筑事务所 atelierd 将协调坚固的蜂窝与人类天马行空的想象力结合，创造了这个“abeilles bee pavilin”.
思考：你知道正六边形的内角和是多少吗？
问题2 你知道长方形和正方形的内角和是多少度？
问题1 三角形的内角和是多少度？
三角形内角和是180°.
问题3 猜想任意四边形的内角和是多少度.
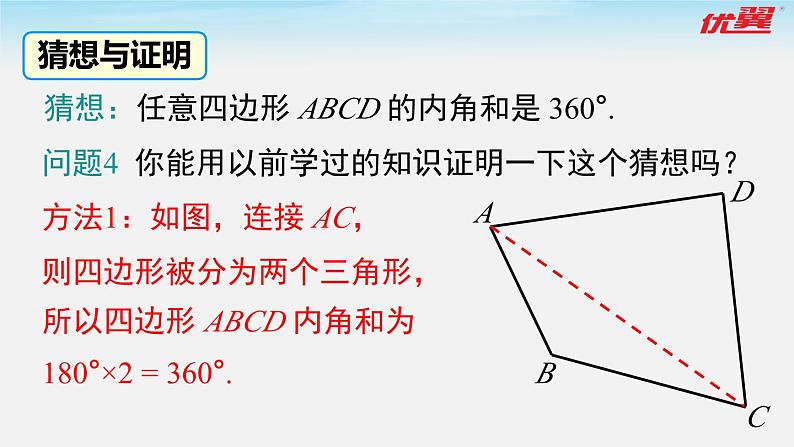
猜想：任意四边形 ABCD 的内角和是 360°.
问题4 你能用以前学过的知识证明一下这个猜想吗？
方法1：如图，连接 AC，则四边形被分为两个三角形，所以四边形 ABCD 内角和为180°×2 = 360°.
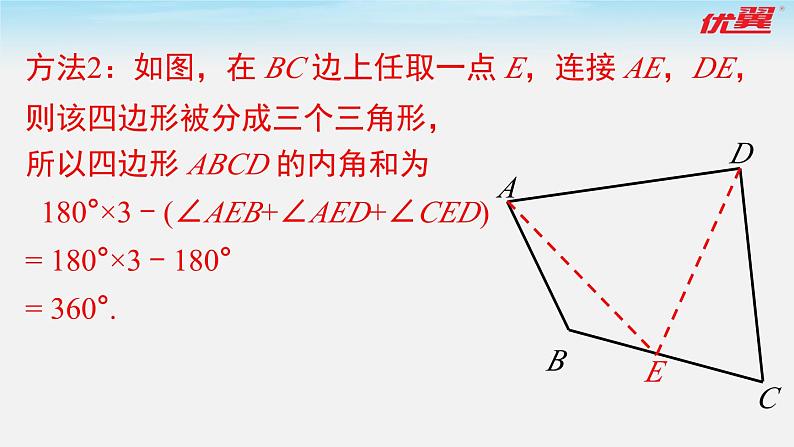
方法2：如图，在 BC 边上任取一点 E，连接 AE，DE，则该四边形被分成三个三角形，所以四边形 ABCD 的内角和为 180°×3 - (∠AEB+∠AED+∠CED)= 180°×3 - 180°= 360°.
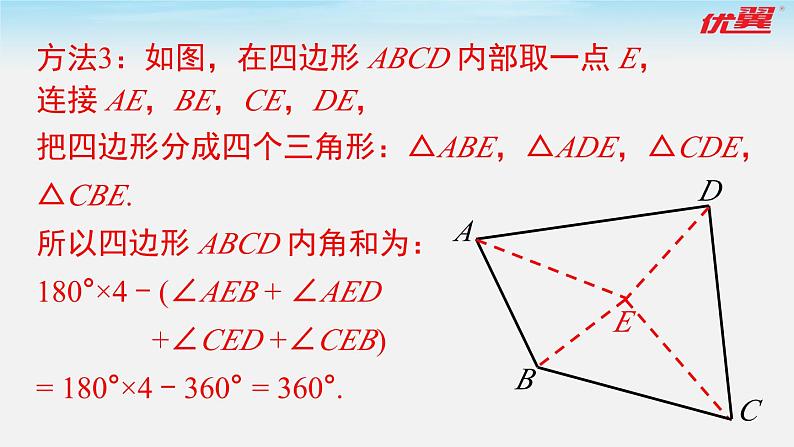
方法3：如图，在四边形 ABCD 内部取一点 E，连接 AE，BE，CE，DE，把四边形分成四个三角形：△ABE，△ADE，△CDE，△CBE.所以四边形 ABCD 内角和为：180°×4 - (∠AEB + ∠AED +∠CED +∠CEB)= 180°×4 - 360° = 360°.
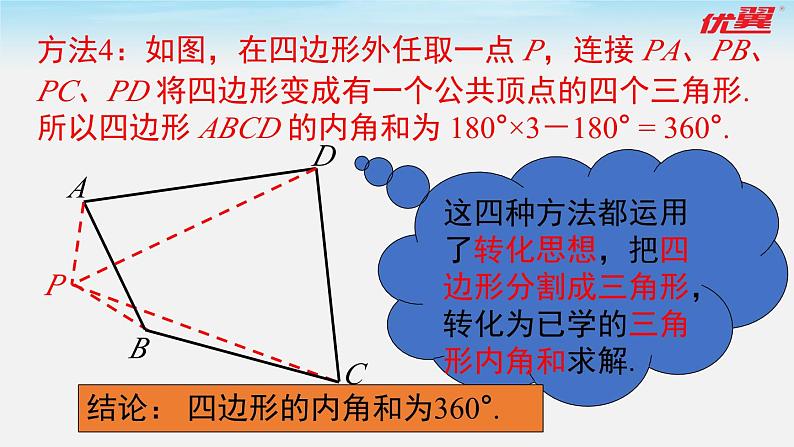
方法4：如图，在四边形外任取一点 P，连接 PA、PB、PC、PD 将四边形变成有一个公共顶点的四个三角形.
所以四边形 ABCD 的内角和为 180°×3－180° = 360°.
这四种方法都运用了转化思想，把四边形分割成三角形，转化为已学的三角形内角和求解.
结论： 四边形的内角和为360°.
例1 如果一个四边形的一组对角互补，那么另一组对角有什么关系？试说明理由.
如图，四边形 ABCD 中，∠A +∠C = 180°.
∠A +∠B +∠C +∠D = 360°，
∠B +∠D = 360°－(∠A +∠C) = 360°－180° = 180°.
如果一个四边形的一组对角互补，那么另一组对角互补.
【变式题】如图，在四边形 ABCD 中，∠A 与∠C 互补，BE 平分∠ABC，DF 平分∠ADC，若 BE∥DF，求证：△DCF 为直角三角形．
证明：在四边形 ABCD 中，∵∠A 与∠C 互补，∴∠ABC +∠ADC = 180°.∵ BE 平分∠ABC，DF 平分∠ADC，∴∠CDF +∠EBF = 90°.∵ BE∥DF，∴∠EBF =∠CFD.∴∠CDF +∠CFD = 90°.故△DCF 为直角三角形．
问题5 你能仿照求四边形内角和的方法，选一种方法求五边形和六边形内角和吗?
内角和为 180°×3 = 540°.
内角和为 180°×4 = 720°.
(n - 2)·180°
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=720°
分割点与多边形的位置关系
n 边形的内角和等于 (n - 2)×180°.
例2 一个多边形的内角和比四边形的内角和多 720°，并且这个多边形的各内角都相等，这个多边形的每个内角是多少度？
解：设这个多边形边数为 n，则 (n - 2)•180 = 360 + 720， 解得 n = 8. ∵ 这个多边形的每个内角都相等， (8 - 2)×180° = 1080°， ∴它每一个内角的度数为 1080°÷8 = 135°.
例3 如图，在五边形 ABCDE 中，∠C = 100°，∠D = 75°，∠E = 135°，AP 平分∠EAB，BP 平分∠ABC，求∠P 的度数．
解析：根据五边形的内角和等于 540°，由∠C，∠D，∠E 的度数可求∠EAB +∠ABC 的度数，再根据角平分线的定义可得∠PAB 与∠PBA 的角度和，进一步求得∠P 的度数．
解：∵∠EAB +∠ABC +∠C +∠D +∠E = 540°，∠C = 100°，∠D = 75°，∠E = 135°，∴∠EAB +∠ABC = 540° - 100° - 75° - 135° = 230°.∵ AP 平分∠EAB，∴∠PAB ＝ ∠EAB.同理可得∠ABP ＝ ∠ABC.∵∠P +∠PAB +∠PBA = 180°，∴∠P = 180°-∠PAB-∠PBA= 180°− (∠EAB +∠ABC) = 180°− ×230° = 65°．
如图，小刚每跑完一圈，身体转过的角度之和是多少？
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角. 如图，∠A 的外角是∠1.
在多边形每个顶点处各取一个外角，它们的和叫做这个多边形的外角和.
如图，在五边形的每个顶点处各取一个外角．
问题1：任意一个外角和它相邻的 内角有什么关系？问题2：五个外角加上它们分别相邻的五个内角和是多少？
5×180° = 900°
－(5－2)×180°
结论：五边形的外角和等于 360°.
问题3：这五个平角和与五边形的内角和、外角和有什么关系？
n 边形的外角和等于 360°.
－(n－2) × 180°
= n 个平角－ n 边形的内角和
思考：n 边形的外角和又是多少呢？
问题4：回想正多边形的性质，你知道正多边形的每 个内角是多少度吗？每个外角呢？为什么？
练一练：(1) 若一个正多边形的内角是 120°，那么这是 正____边形.(2) 已知某正多边形的每个外角都是 45°，则这个多边形 是______边形.
例4 已知一个多边形，它的内角和等于外角和的 2 倍， 求这个多边形的边数.
解：设多边形的边数为 n. ∵它的内角和等于 (n - 2)•180°， 多边形外角和等于 360°， ∴ (n - 2)•180° = 2×360°， 解得 n = 6. ∴ 这个多边形的边数为 6.
例5 已知一个多边形的每个内角与外角的比都 是 7∶2，求这个多边形的边数.
解法一：设这个多边形的内角为 7x°，外角为 2x°，根据题意得
7x + 2x = 180，
解得 x = 20.
即每个内角是 140°，每个外角是 40°.
360°÷40° = 9.
答：这个多边形的边数为 9.
解法二：设这个多边形的边数为 n ，根据题意得
【变式题】一个正多边形的一个外角比一个内角大60°，求这个多边形的每个内角的度数及边数．
解：设该正多边形的内角是 x°，外角是 y°，则得到一个方程组 解得而任何多边形的外角和是 360°，则该正多边形的边数为 360÷120 = 3.故这个多边形的每个内角的度数是 60°，边数是 3．
例6 如图，在正五边形 ABCDE 中，连接 BE，求∠BED 的度数．
解：由题意得AB = AE，所以∠AEB = (180° - ∠A) = 36°，所以∠BED = ∠AED -∠AEB = 108° - 36° = 72°.
1. 判断对错：(1)当多边形边数增加时，它的内角和也随着增加.( )(2)当多边形边数增加时，它的外角和也随着增加.( )(3)三角形的外角和与八边形的外角和相等． ( )
2. 一个正多边形的内角和为 720°，则这个正多边形的每一个内角等于_____．
3. 如图所示，小华从点 A 出发，沿直线前进 10 米后左转 24°，再沿直线前进 10 米，又向左转 24°……照这样走下去，他第一次回到出发地点 A 时，走的路程一共是______米．
4. 一个多边形的内角和不可能是（ ） A. 1800° B. 540° C. 720° D. 810°
5. 一个多边形从一个顶点可引对角线 3 条，这个多边形 内角和等于（ ） A. 360° B. 540° C. 720° D. 900°
6. 一个多边形的内角和为 1800°，截去一个角后，求得到的多边形的内角和.
解：∵ 1800÷180 ＝ 10，∴ 原多边形边数为10＋2 ＝ 12.∵ 一个多边形截去一个内角后，边数可能减 1，可能不变，也可能加 1，即新多边形的边数可能是 11，12，13，∴ 新多边形的内角和可能是 1620°，1800°，1980°.
能力提升：如图，求∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7的度数.
解：如图，∵∠3＋∠4＝∠8＋∠9，∴∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＝ ∠1＋∠2＋∠8＋∠9＋∠5＋∠6＋∠7＝ 五边形的内角和 ＝ 540°.
(n - 2) ×180°(n≥3的整数)
多边形的外角和等于 360°.特别注意：与边数无关.
欢迎各位老师对此课件提出宝贵的建议，我们将更好的为您服务。
扫描二维码，添加我的企业微信吧~
如果您有兴趣参与课件编写，请扫码添加教育产品顾问李老师微信~
感谢您使用我们的课件！