（期末押题卷）期末质量检测拓展卷-2022-2023学年五年级下册数学高频易错题（人教版）

这是一份（期末押题卷）期末质量检测拓展卷-2022-2023学年五年级下册数学高频易错题（人教版），共17页。试卷主要包含了拼图形等内容，欢迎下载使用。

（期末押题卷）期末质量检测拓展卷
2022-2023学年五年级下册数学高频易错题（人教版）
一．选择题（共9小题）
1．妈妈已经织了一件毛衣的56，可以转变成（　　）
A．织了的是剩下的16 B．剩下的是织了的16
C．剩下的是毛衣的15 D．剩下的是织了的15
2．用一张长方形纸折一折，可以围成一个正方体或一个长方体（如图），围成的长方体和正方体，谁的体积大？（　　）
​
A．长方体体积大 B．正方体体积大
C．一样大 D．无法比较
3．把三个小正方体拼成一个长方体，这个长方体与原来相比，（　　）
A．总体积变小，表面积变小
B．总体积不变，表面积变小
C．总体积变大，表面积变大
D．总体积不变，表面积不变
4．拼图形：淘气将两个相同的正方体拼成了一个长方体，拼成的长方体表面积比原来两个正方体的表面积之和减少了18平方分米，原来每个正方体的表面积是（　　）平方分米。
A．36 B．54 C．72 D．108
5．把一个长方体分成几个小长方体后，所有小长方体的表面积之和与原长方体的表面积相比，（　　）
A．不变 B．变大 C．变小
6．淘气和妹妹手拉手一起从家出发去上学，途中淘气发现忘带作业本，于是他跑回家，找到作业本后向学校飞奔而去刚好在校门口追上了妹妹。如图正确描述淘气和妹妹上学路上情景的是（　　）
A．B． C．
7．一个长方体的长、宽、高都扩大到原来的2倍，它的表面积就 （　　）
A．扩大到原来的4倍 B．扩大到原来的8倍
C．扩大到原来的2倍
8．下面被布遮着的是一个长方体，这个长方体表面被布遮去了（　　）个直角。

A．4 B．8 C．12
9．下面的数既是奇数又是3、5的倍数的数是（　　）
A．35 B．60 C．105 D．120
二．填空题（共7小题）
10．做一个长12cm、宽7cm、高6cm的长方体铁丝框架，至少需要 　 　cm的铁丝。
11．有12支铅笔，平均分给2个同学。每支铅笔是铅笔总数的 　 　，每人分得的铅笔是总数的 　 　。（填分数）
12．A＝2×2×3×5，B＝2×3×5×7，那么A和B的最大公因数是 　 　，最小公倍数是 　 　。
13．42是一个数的倍数，70也是这个数的倍数，这个数最大是 　 　。
14．一根长3m的长方体钢材，沿横截面截成三段后，表面积增加了1.6dm2，这根长方体钢材的体积是 　 　dm3。
15．“一节课的时间是23小时，做练习占了这节课的12”。这句话中，“23小时”是把 　 　看作单位“1”，“12”是把 　 　看作单位“1”。
16．一个数的最小倍数是16，这个数是 　 　，它的因数有 　 　。
三．判断题（共9小题）
17．假分数都不小于1　 　（判断对错）
18．两个自然数（0除外）的积一定是这两个数的公倍数。 　 　（判断对错）
19．体积是200cm3保温杯，它的容积比200mL大。 　 　（判断对错）
20．一个正方体的棱长扩大3倍，它的体积扩大9倍。 　 　（判断对错）
21．一个长方体分成几个小长方体后，计算几个小长方体的表面积和与体积和，与大长方体相比没有变化。　 　 　（判断对错）
22．正方体的棱长扩大2倍，棱长和扩大2倍，表面积扩大2倍。 　 　（判断对错）
23．笑笑喝了一杯牛奶的34，淘气也喝了一杯牛奶的34，他俩喝的一样多．　 　．（判断对错）
24．长方体、正方体有体积，不规则的物体也有体积。 　 　（判断对错）
25．把一个蛋糕切成4份，每份是它的14．　 　．（判断对错）
四．计算题（共4小题）
26．求下面各组数的最大公因数。
32和1
12和18
72和36
20和15
27．把下面每组中的两个分数通分。
59和712
38和59
316和712
28．用你喜欢的方法计算。
12+12-310
8-1519-419
725+(518+1825)
1013+15+313+45
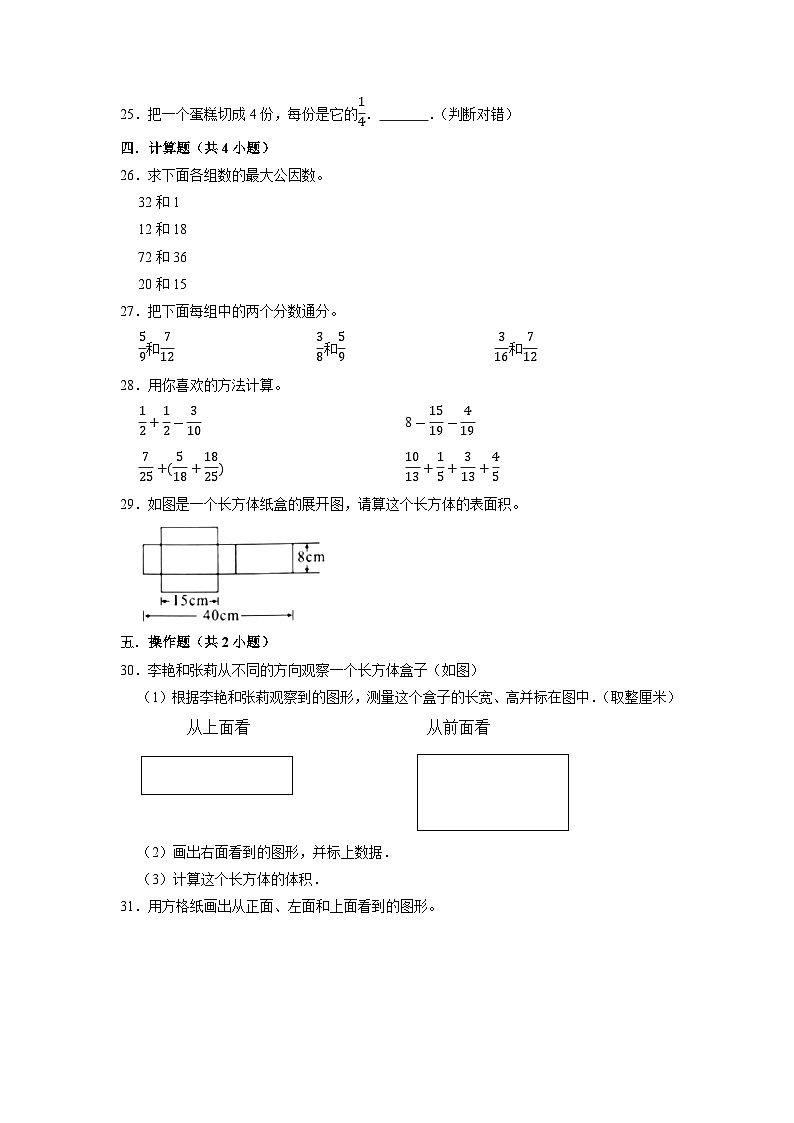
29．如图是一个长方体纸盒的展开图，请算这个长方体的表面积。

五．操作题（共2小题）
30．李艳和张莉从不同的方向观察一个长方体盒子（如图）
（1）根据李艳和张莉观察到的图形，测量这个盒子的长宽、高并标在图中．（取整厘米）

（2）画出右面看到的图形，并标上数据．
（3）计算这个长方体的体积．
31．用方格纸画出从正面、左面和上面看到的图形。

六．应用题（共8小题）
32．一个带盖的长方体木箱，体积是576立方分米。它的长是12分米，宽是8分米，做这样一个木箱至少要用木板多少平方分米？
33．一个长方体的空油箱，它的长、宽、高分别是5dm、4dm、3dm，向油箱中加入56L汽油，油箱加满了吗？如果每升汽油7.5元，则这次加油一共需要多少钱？

34．一个长、宽、高分别为36厘米、20厘米、15厘米的小纸箱，在所有的棱上粘上一圈胶带，至少需要多长的胶带？
35．笑笑家正在装修新房，经过测量可知，她家的卫生间长5米，宽2米，高2.7米，门窗的面积为2.5平方米。要在卫生间的四周墙壁贴上墙砖，贴墙砖的高度为2.5米，请你帮忙算一算，贴墙砖的面积至少有多少平方米？

36． 兴华小学要粉刷一间美术教室的四面墙壁和天花板。美术教室的长是8m，宽是6m，高3m。门窗的面积是12.2m2。如果每平方米需要花5元涂料费，那么粉刷这间美术教室要花多少元？

37．学校要粉刷一间教室的四壁和天花板。已知教室的长是9米，宽7米，高是3米，扣除门窗的面积12.5平方米，要粉刷的面积是多少平方米？
38．蛋糕店里做了113块蛋糕，如果每3块装一盒，能正好装完吗？如果不能，至少还要再做几个这样的蛋糕就能正好装完了？
39．一个房间的长为6米、宽为4米、高为3米，门窗的面积是6平方米，现在要粉刷这个房间的四壁和屋顶，粉刷的面积有多大？如果1平方米需要涂料0.9千克，那么一共需要多少千克涂料？

（期末押题卷）期末质量检测拓展卷
2022-2023学年五年级下册数学高频易错题（人教版）
参考答案与试题解析
一．选择题（共9小题）
1．【答案】D
【分析】把这件毛衣看作单位“1”，已经织了一件毛衣的56，还剩下（1-56），用剩下的除以织的分数即可判断。
【解答】解：（1-56）÷56
=16÷56
=15
答：剩下的是织了的15。
故选：D。
【点评】本题主要考查了分数的意义及除法的灵活运用。
2．【答案】B
【分析】根据题意可知：以长方形的长边a作底面周长，宽边b作高，分别可以围成一个长方体、正方体，再根据它们的体积＝底面积×高，高相同，底面积越大，体积就越大，因为正方体的底面积大，所以正方体的体积大；据此解答即可。
【解答】解：分析可知，用一张长方形纸折一折，可以围成一个正方体或一个长方体（如图），围成的长方体和正方体，正方体的体积大。
故选：B。
【点评】本题考查了图形的拼组以及长方体的体积和正方体的体积知识，结合题意分析解答即可。
3．【答案】B
【分析】根据正方体、长方体的表面积、体积的意义可知，把三个小正方体拼成一个长方体，这个长方体的体积等于原来3个正方体的体积和，这个长方体的表面积比原来3个正方体的表面积减少了正方体的4个面的面积。据此解答。
【解答】解：把三个小正方体拼成一个长方体，这个长方体与原来相比，体积不变，表面积变小。
故选：B。
【点评】此题考查的目的是理解掌握正方体、长方体的表面积、体积的意义及应用。
4．【答案】B
【分析】根据题意可知，将两个相同的正方体拼成了一个长方体，拼成的长方体表面积比原来两个正方体的表面积之和减少了18平方分米，也就是拼成的长方体表面积比原来两个正方体的表面积之和减少了正方体的2个面的面积，据此可以求出正方体的一个面的面积，然后根据正方体的表面积公式：S＝6a2，把数据代入公式解答。
【解答】解：18÷2×6
＝9×6
＝54（平方分米）
答：原来每个正方体的表面积是54平方分米。
故选：B。
【点评】此题主要考查长方体、正方体表面积公式的灵活运用，关键是熟记公式。
5．【答案】B
【分析】根据长方体表面积的意义，围成长方体的6个面的总面积叫作长方体的表面积。由此可知，把一个长方体分成几个小长方体后，所有小长方体的表面积之和与原长方体的表面积相比，表面积变大了。据此解答即可。
【解答】解：由分析可得：把一个长方体分成几个小长方体后，所有小长方体的表面积之和与原长方体的表面积相比，变大了。
故答案为：B。
【点评】此题考查的目的是理解掌握长方体表面积的意义及应用。
6．【答案】A
【分析】根据题意可知，妹妹没有停留一直走到学校，所以表示妹妹行走的图象是一条直线，淘气和妹妹一起去上学，所以他们一开始的图象是重合在一起的，途中淘气发现忘带作业本，于是他跑回家，拿好作业本，表示淘气行走的图象是一条折线，且在家中拿作业本这段时间形走的距离不变，然后马上向学校飞奔而去，刚好在校门口追上了妹妹。这时表示他们两人行走的图象交于一点，据此对照下面的图象进行选择即可。
【解答】解：由分析得：所以表示妹妹行走的图象是一条直线，表示淘气行走的图象，途中返回是折线，且在家中拿作业本这段时间形走的距离不变，然后马上向学校飞奔而去，刚好在校门口追上了妹妹。这时表示他们两人行走的图象交于一点。由此可知，图A描述的是淘气和妹妹上学路上的情景。
故选：A。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用，并且能够根据统计图提供的信息，解决有关的实际问题。
7．【答案】A
【分析】根据长方体的表面积＝（长×宽+长×高+宽×高）×2，再根据因数与积的变化规律，积扩大到原来的倍数等于因数扩大到原来倍数的乘积。据此解答即可。
【解答】解：2×2＝4
所以一个长方体的长、宽、高都扩大到原来的2倍，它的表面积就扩大到原来的4倍。
故选：A。
【点评】此题主要根据长方体的表面积的计算方法和积的变化规律解决问题，使学生明确积扩大的倍数等于因数扩大倍数的乘积。
8．【答案】C
【分析】根据直角的意义，90度的角叫做直角；长方体的一个顶点由三条棱互相垂直相交，所以在长方体的一个顶点有3个直角；这个长方体表面被布遮住了4个顶点，所以被遮住了12个直角；据此解答。
【解答】解：长方体的一个顶点由三条棱互相垂直相交，所以在长方体的一个顶点有3个直角，所以这个长方体表面被布遮住了4个顶点，所以被遮住了12个直角。
故选：C。
【点评】此题考查的目的是理解掌握直角的意义，长方体的特征，关键是明确：长方体的一个顶点由三条棱互相垂直相交，所以在长方体的一个顶点有3个直角。
9．【答案】C
【分析】各个数位上的数字相加的和能被3整除的数这个数能被3整除；个位数为0或5的数能被5整除；不是2的倍数的数叫做奇数；据此可知：这个数的个位是5，各个数位上的数字相加的和能被3整除；据此解答即可。
【解答】解：这个数的个位是5，各个数位上的数字相加的和能被3整除；所以这个数是105。
故选：C。
【点评】本题考查了奇数的定义、3和5整除的数的特征及灵活运用。
二．填空题（共7小题）
10．【答案】100。
【分析】用铁丝做一个长方体框架，求铁丝的长度就是求长方体的棱长总和；根据长方体的棱长总和＝（长+宽+高）×4，代入数据计算即可。
【解答】解：（12+7+6）×4
＝25×4
＝100（cm）
答：至少需要100cm的铁丝。
故答案为：100。
【点评】本题考查长方体棱长总和的公式的运用。
11．【答案】112，12。
【分析】把这些铅笔的支数（12支）看作单位“1”，求每支是总支数的几分之几，用1除以12；
求每人分得的铅笔是总数的几分之几，用1除以2（或先用总支数除以人数求出每人分得的支数，再用每人分得的支数除以总支数）。
【解答】解：1÷12=112
1÷2=12
答：每支铅笔是铅笔总数的112，每人分得的铅笔是总数的12。
故答案为：112，12。
【点评】本题主要考查分数的意义，注意找准单位“1”，分清以谁为标准量。
12．【答案】30，420。
【分析】根据求两个数的最大公因数、求两个数的最小公倍数的方法，两个数公有质因数连乘积是它们的最大公因数，两个数公有质因数与每个数独有质因数的连乘积是它们的最小公倍数。据此解答。
【解答】解：a＝2×2×3×5；
b＝2×3×5×7；
a和b的最大公因数是2×3×5＝30；
a和b的最小公倍数是2×5×3×2×7＝420。
故答案为：30，420。
【点评】此题考查的目的是理解掌握求两个数的最大公因数、求两个数的最小公倍数的方法及应用。
13．【答案】14。
【分析】根据题意，42是一个数的倍数，70也是这个数的倍数，那么这个数是42和70的公因数，求这个数最大是多少，就是求这个数的最大公因数。
【解答】解：42＝2×3×7
70＝2×5×7
42和70的最大公因数是：2×7＝14
所以42是一个数的倍数，70也是这个数的倍数，这个数最大是14。
故答案为：14。
【点评】此题需要学生熟练掌握求两个数最大公因数的方法并灵活运用。
14．【答案】12。
【分析】根据题意可知，把这根长方体钢材，横截成三段后，表面积比原来增加4个截面的面积，据此可以求出长方体的底面积，再根据长方体的体积公式；V＝Sh，把数据代入公式解答。
【解答】解：3米＝30分米
1.6÷4×30
＝0.4×30
＝12（立方分米）
答：这根长方体钢材的体积是12立方分米。
故答案为：12。
【点评】此题主要考查长方体的表面积公式、体积公式的灵活运用，关键是熟记公式。
15．【答案】1小时，23小时。
【分析】通常把“的”前面的量以及“是”、“比”、“占”、“相当于”等后面的量看作单位“1”，根据题意可知，“一节课的时间是23小时，做练习占了这节课的12”。这句话中，“23小时”是把 1小时看作单位“1”，“12”是把“23小时”看作单位“1”。据此解答。
【解答】解：“一节课的时间是23小时，做练习占了这节课的12”。这句话中，“23小时”是把1小时看作单位“1”，“12”是把23小时看作单位“1”。
故答案为：1小时，23小时。
【点评】此题考查了判断单位“1”的方法，应注意灵活运用。
16．【答案】16；1、2、4、8、16。
【分析】一个数的最大因数和最小倍数都是它本身，再利用找一个数因数的方法一对一的找出所有的因数。
【解答】解：一个数的最小倍数是16，这个数是16；
16＝1×16＝2×8＝4×4；
所以16的因数有：1、2、4、8、16。
故答案为：16；1、2、4、8、16。
【点评】掌握求一个数因数的方法是解答题目的关键。
三．判断题（共9小题）
17．【答案】见试题解答内容
【分析】假分数是分子大于或等于分母的分数，当分子大于分母时，分数值大于1；当分子等于分母时，分数值等于1．所以假分数的分数值大于或等于1．即假分数不小于1．
【解答】解：当分子大于分母时，分数值大于1；当分子等于分母时，分数值等于1．
所以假分数的分数值大于或等于1．
即假分数不小于1．
故答案为：√．
【点评】本题主要根据假分数的意义进行解答．
18．【答案】√
【分析】如果a和b是两个数不为0的自然数，a×b＝c，则a和b都是c的因数，c即是a的倍数，也是b的倍数，c是a和b公共的倍数，所以c是a和b这两个数的公倍数。
【解答】解：两个数（不为0的自然数）的积一定是这两个数的公倍数。所以原题说法正确。
故答案为：√。
【点评】此题主要考查因数和倍数、公倍数的意义。
19．【答案】×
【分析】物体所占空间的大小叫做物体的体积，容器所能容纳物体的体积叫做它的容积，保温杯有厚度，如果保温杯的体积是200cm3，那么保温杯的容积一定小于200cm3，据此解答。
【解答】解：200cm3＝200mL，体积是200cm3保温杯，它的容积一定比200mL小。原题干说法错误。
故答案为：×。
【点评】体积是从物体的外部测量长、宽、高，容积需要从物体内部测量长、宽、高，不忽略物体厚度时，物体的体积一定大于容积。
20．【答案】×
【分析】根据正方体的体积公式：V＝a3，再根据因数与积的变化规律，积扩大到原来的倍数等于因数扩大到原来倍数的乘积。据此判断。
【解答】解：3×3×3＝27
所以一个正方体的棱长扩大3倍，它的体积扩大27倍。
因此题干中的结论是错误的。
故答案为：×。
【点评】此题主要考查正方体体积公式的灵活运用，积的变化规律及应用。
21．【答案】×
【分析】根据长方体的表面积、体积的意义可知，把一个长方体分成几个小长方体后，这几个小长方体的表面积和大于原来长方体的表面积，这几个小长方体的体积和等于原来长方体的体积。据此判断。
【解答】解：把一个长方体分成几个小长方体后，这几个小长方体的表面积和大于原来长方体的表面积，这几个小长方体的体积和等于原来长方体的体积。
因此题干中的结论是错误的。
故答案为：×。
【点评】此题考查的目的是理解掌握长方体的表面积、体积的意义及应用。
22．【答案】×
【分析】根据正方体的棱长总和＝棱长×12，正方体的表面积＝棱长×棱长×6，再根据积的变化规律可知，正方体的棱长扩大到原来的2倍，棱长总和就扩大到原来的2倍，正方体的表面积就扩大到原来的（2×2）倍。据此判断。
【解答】解：正方体的棱长扩大到原来的2倍，棱长总和就扩大到原来的2倍，正方体的表面积就扩大到原来的4倍。
因此，题干中的结论是错误的。
故答案为：×。
【点评】此题主要考查正方体的棱长总和公式、表面积公式的灵活运用，积的变化规律及应用。
23．【答案】见试题解答内容
【分析】由于两个杯子的大小不能确定，所以无法比较他们喝的牛奶谁喝的多；根据分数的意义可知，如果两个杯子一样大，则喝的一样多；如果不同则喝的不一样多，然后再进一步判断即可．
【解答】解：根据分数的意义可知，
由于两个杯子的大小不能确定，
所以无法比较他们喝的牛奶谁喝的多．
故答案为：×．
【点评】只有在单位“1”相同的情况下，才能根据两个分率占单位“1”的多少进行比较．
24．【答案】√
【分析】根据体积的意义，物体所占空间的大小叫做物体的体积。据此判断。
【解答】解：根据分析可知，长方体、正方体有体积，不规则的物体也有体积。此说法是正确的。
故答案为：√。
【点评】正确理解体积的意义，是解答此题的关键。
25．【答案】×
【分析】将单位“1”平均分成若干份，表示其中这样一份或几份的数叫分数．由于“把一个蛋糕切成4份”没有说明是“平均分”，根据分数的意义，每份是它的14的说法是错误的．
【解答】解：由于“把一个蛋糕切成4份”没有说明是“平均分”，根据分数的意义，
把一个蛋糕切成4份，每份是它的14的说法是错误的．
故答案为：×．
【点评】在理解分数的意义的时候，要注意“平均分”这个要素．
四．计算题（共4小题）
26．【答案】1，6，36，5。
【分析】（1）32和1两个是互质数，是互质数的两个数，它们的最大公因数是1，据此解答即可；
（2）对于一般的18和12，20和15这两组数来说，这两个数的公有质因数的连乘积是这两个数的最大公约数，由此解答；
（3）因为72÷36＝2，即72和36成倍数关系，当两个数成倍数关系时，较小的那个数是这两个数的最大公因数；据此解答即可。
【解答】解：（1）32和1互为质数，它们的最大公因数是1，
（2）12＝2×2×3，18＝2×3×3，所以12和18的最大公因数是6，
（3）因为72÷36＝2，即72和36成倍数关系，当两个数成倍数关系时，较小的那个数是这两个数的最大公因数，所以最大公因数是36，
（4）20＝2×2×5，15＝3×5，所以20和15的最大公因数是5，
【点评】此题主要考查了求两个数的最大公因数：对于一般的两个数来说，这两个数的公有质因数连乘积是最大公因数；对于两个数为倍数关系时的最大公因数，最大公因数为较小的数，较大的那个数是这两个数的最小公倍数；是互质数的两个数，它们的最大公因数是1。
27．【答案】2036；2136；2772；4072；948；2848。
【分析】根据两个分数的分母相同但不改变原数大小的过程。先求出原来几个分母的最小公倍数，然后把各分数分别化成用这个最小公倍数作分母的分数。
【解答】解：（1）59=5×49×4=2036
712=7×312×3=2136
（2）38=3×98×9=2772
59=5×89×8=4072
（3）316=3×316×3=948
712=7×412×4=2848
【点评】本题主要考查异分母分数的通分方法。
28．【答案】710；7；1518；2。
【分析】12+12-310，先算加法，再算减法；
8-1519-419，运用减法的性质简算；
725+（518+1825），运用加法交换律、加法结合律简算；
1013+15+313+45，运用加法交换律、加法结合律简算。
【解答】解：12+12-310
=1-310
=710
8-1519-419
＝8﹣（1519+419）
＝8﹣1
＝7
725+（518+1825）
=518+（725+1825）
=518+1
=1518
1013+15+313+45
＝（1013+313）+（15+45）
＝1+1
＝2
【点评】此题考查的目的是理解掌握分数加减混合运算的顺序以及它们的计算法则，并且能够灵活选择简便方法进行计算。
29．【答案】470平方厘米。
【分析】通过观察长方体的展开图可知，这个长方体的长是15厘米，宽是8厘米，高是（40÷2﹣15）厘米，根据长方体的表面积公式：S＝（ab+ah+bh）×2，把数据代入公式解答。
【解答】解：长方体的高：
40÷2﹣15
＝20﹣15
＝5（厘米）
（15×8+15×5+8×5）×2
＝（120+75+40）×2
＝235×2
＝470（平方厘米）
答：这个长方体的表面积是470平方厘米。
【点评】此题考查的目的是理解掌握长方体展开图的特征及应用，长方体的表面积公式及应用，关键是熟记公式，重点是求出长方体的高。
五．操作题（共2小题）
30．【答案】见试题解答内容
【分析】（1）上面的长等于长方体的长，上面的宽等于长方体的宽，前面的宽等于长方体的高．
（2）长方体右面的长等于长方体的高、右面的宽等于长方体的宽，据此再图即可．
（3）根据长方体的体积公式：V＝abh，把数据代入公式解答．
【解答】解：（1）如图：

（2）作图如下：右面的长是1.8厘米，宽是0.9厘米．

（3）3.4×0.9×1.8
＝3.06×1.8
＝5.508（立方厘米），
答：这个长方体的体积是5.508立方厘米．
【点评】此题考查的目的是理解掌握长方体展开图的特征，以及长方体的体积公式的灵活运用．
31．【答案】
【分析】从正面看到的图形有2层，第一层有2个正方形，第二层有1个正方形，左对齐；
从上面看到的图形有2层，第一层有1个正方形，第二层有2个正方形，右对齐；
从左面看到的图形有2层，第一层有2个正方形，第二层有1个正方形，左对齐。
【解答】解：如图：

【点评】本题主要考查从不同方向观察物体，培养学生的空间想象能力。
六．应用题（共8小题）
32．【答案】432平方分米。
【分析】根据长方体的体积公式：V＝abh，那么h＝V÷ab，据此求出高，再根据长方体的表面积公式：S＝（ab+ah+bh）×2，把数据代入公式解答。
【解答】解：576÷（12×8）
＝576÷96
＝6（分米）
（12×8+12×6+8×6）×2
＝（96+72+48）×2
＝216×2
＝432（平方分米）
答：做这样一个木箱至少要用木板432平方分米。
【点评】此题主要考查长方体的体积公式、表面积公式的灵活运用，关键是熟记公式，重点是求出长方体的高。
33．【答案】没有加满，420元。
【分析】根据长方体的体积（容积）公式：V＝abh，把数据代入公式求出这个油箱的容积，然后与56升进行比较即可。然后根据单价×数量＝总价，列式解答。
【解答】解：5×4×3
＝20×3
＝60（立方分米）
60立方分米＝60升
56升＜60升
7.5×56＝420（元）
答：油箱没有加满，这次加油一共需要420元。
【点评】此题主要考查长方体的体积（容积）公式的灵活运用，关键是熟记公式。
34．【答案】284厘米。
【分析】根据长方体的棱的特征，12条棱中互相平行的一组4条棱的长度相等，它的棱长总和＝（长+宽+高）×4；由此解答。
【解答】解：（36+15+20）×4
＝71×4
＝284（厘米）
答：至少需要284厘米长的胶带。
【点评】此题主要考查长方体的特征及棱长总和的计算方法。
35．【答案】20平方米。
【分析】根据题意可知，在卫生间的四周墙壁贴上墙砖，贴墙砖的高度为2.5米，门窗的面积为2.5平方米，求出4面墙壁贴瓷砖的面积，再减去门窗面积即可。
【解答】解：5×2.5×2+2×2.5×2﹣2.5
＝12.5+10﹣2.5
＝22.5﹣2.5
＝20（平方米）
答：贴瓷砖的面积至少有20平方米。
【点评】此题考查的目的是理解长方体表面积的意义，掌握长方体的表面积公式及应用，关键是弄清需要求哪几个面的面积，缺少的是哪些面。
36．【答案】599元。
【分析】根据题意可知，美术教室的地面不需要粉刷，也就是需要粉刷美术教室的天花板和4面墙壁（门窗面积除外），根据无底长方体的表面积公式：S＝ab+ah×2+bh×2，把数据代入公式求出这5个面的总面积，再减去门窗面积就是需要粉刷的面积，然后用粉刷的面积乘每平方米的费用即可。
【解答】解：8×6+8×3×2+6×3×2
＝48+48+36
＝132（平方米）
132﹣12.2＝119.8（平方米）
119.8×5＝599（元）
答：粉刷这间美术教室要花599元。
【点评】此题主要考查长方体表面积公式的灵活运用，关键是明确：需要粉刷的是哪几个面。
37．【答案】146.5平方米。
【分析】先搞清这道题是求长方体的表面积，其次这个长方体的表面由五个长方形组成，缺少下面，最后计算这五个面的面积减去门窗的面积，列式解答即可。
【解答】解：9×7+9×3×2+7×3×2﹣12.5
＝63+54+42﹣12.5
＝159﹣12.5
＝146.5（平方米）
答：粉刷的面积是146.5平方米。
【点评】这是一道长方体表面积的实际应用，在计算时要分清需要计算几个长方形面的面积，缺少的是哪一个面的面积，从而列式解答即可。
38．【答案】不能正好装完，如果每3块装一盒，至少还需要加上1块蛋糕。
【分析】先计算一下113能不能被3整除，如果能，就能正好装完，反之，则不能；求至少还需几个，先求出余数，然后用除数减去余数，即至少买的个数。
【解答】解：113÷3＝37（盒）……2（块）
至少增加：3﹣2＝1（块）
答：不能正好装完，如果每3块装一盒，至少还需要加上1块蛋糕。
【点评】此题主要考查根据能被3整除的数的特征解决问题。
39．【答案】78平方米，70.2千克。
【分析】根据无底长方体的表面积公式：S＝ab+2ah+2bh，把数据代入公式求出4面墙壁和顶棚的总面积，减去门窗面积就是需要粉刷的面积，然后用粉刷的面积乘每平方米用涂料的质量即可。
【解答】解：6×4+6×3×2+4×3×2﹣6
＝24+36+24﹣6
＝84﹣6
＝78（平方米）
78×0.9＝70.2（千克）
答：粉刷的面积有78平方米，一共需要70.2千克涂料。
【点评】此题主要考查长方体表面积公式的灵活运用，关键是熟记公式。
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/6/13 17:09:55；用户：李家祯；邮箱：hfnxxx59@qq.com；学号：47467572