






新教材适用2024版高考数学一轮总复习第7章立体几何第2讲空间点直线平面之间的位置关系课件
展开第二讲 空间点、直线、平面之间的位置关系
知识梳理 · 双基自测
知识点一 平面的基本性质基本事实1.____________的三点确定一个平面.基本事实2.如果一条直线上的____________在一个平面内,那么这条直线在这个平面内.基本事实3.如果两个不重合的平面有一个公共点,那么它们有且________________________的公共直线.
推论1.经过一条直线和________________________,有且只有一个平面.推论2.经过两条_________直线,有且只有一个平面.推论3.经过两条_________直线,有且只有一个平面.
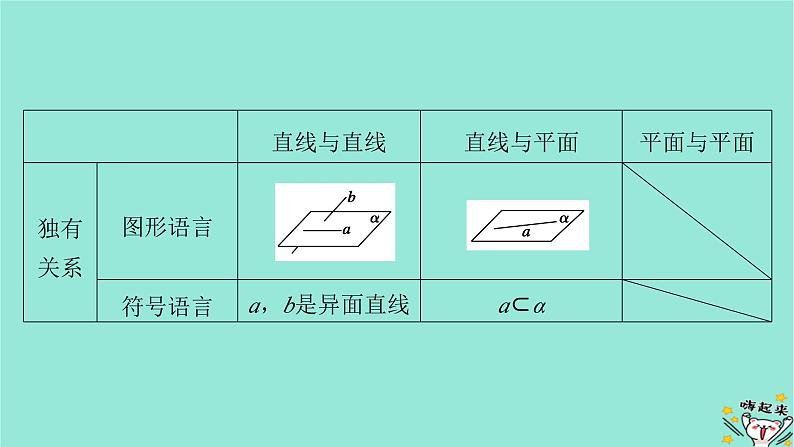
知识点二 空间点、直线、平面之间的位置关系
知识点三 异面直线所成角、基本事实4及等角定理(1)异面直线所成的角①定义:设a,b是两条异面直线,经过空间中任一点O作直线a′∥a,b′∥b,把a′与b′所成的__________________叫做异面直线a与b所成的角.
(2)基本事实4.(平行公理)平行于同一条直线的两条直线_________.(3)等角定理空间中如果两个角的两边分别对应平行,那么这两个角__________.
异面直线的判定定理过平面内一点与平面外一点的直线和这个平面内不经过该点的直线是异面直线.用符号可表示为:若l⊂α,A∉α,B∈α,B∉l,则直线AB与l是异面直线(如图).
题组一 走出误区1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)如果两个不重合的平面α,β有一条公共直线a,就说平面α,β相交,并记作α∩β=a.( )(2)两个平面α,β有一个公共点A,就说α,β相交于过A点的任意一条直线.( )(3)如果两个平面有三个公共点,则这两个平面重合.( )
(4)经过两条相交直线,有且只有一个平面.( )(5)两两相交的三条直线共面.( )(6)若a,b是两条直线,α,β是两个平面,且a⊂α,b⊂β,则a,b是异面直线.( )
题组二 走进教材2.(必修2P147例1)如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是AB,AD的中点,则异面直线B1C与EF所成角的大小为( )A.30° B.45° C.60° D.90°
[解析] 连接B1D1,D1C,则B1D1∥EF,故∠D1B1C即为所求的角.又B1D1=B1C=D1C,∴△B1D1C为等边三角形,∴∠D1B1C=60°.故选C.
3.(必修2P134例1)如图,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA上的点.
(2)若E、F、G、H分别为棱AB、BC、CD、DA的中点,①当AC,BD满足条件__________________时,四边形EFGH为菱形;②当AC,BD满足条件______________________时,四边形EFGH为正方形.
AC=BD且AC⊥BD
题组三 走向高考4. (2019·新课标Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则( )A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线
[解析] 连BD、BE,则BD过点N,∵点N为正方形ABCD的中心,△ECD为正三角形,M是线段ED的中点,∴BM⊂平面BDE,EN⊂平面BDE,∵BM是△BDE中DE边上的中线,EN是 △BDE中BD边上的中线,∴直线BM,EN是相交直线,
[解析] 解法一:如图,连接BC1,PC1,因为AD1∥BC1,所以∠PBC1或其补角为直线PB与AD1所成的角,因为BB1⊥平面A1B1C1D1,所以BB1⊥PC1,又PC1⊥B1D1,BB1∩B1D1=B1,
考点突破 · 互动探究
如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是AB,AA1的中点.求证:(1)E,C,D1,F四点共面;(2)CE,D1F,DA三线共点.
[解析] (1)如图,连接EF,CD1,A1B.因为E,F分别是AB,AA1的中点,所以EF∥A1B.又A1B∥CD1,所以EF∥CD1,所以E,C,D1,F四点共面.
(2)因为EF∥CD1,EF
2.点、线共面的常用判定方法(1)纳入平面法:先确定一个平面,再证明有关点、线在此平面内.(2)将所有条件分为两部分,然后分别确定平面,再证两平面重合.3.证明线共点问题的常用方法是:先证其中两条直线交于一点,再证其他直线经过该点.
〔变式训练1〕(多选题)如图是正方体或四面体,P,Q,R,S分别是所在棱的中点,这四个点共面的是( )
[解析] 在A图中分别连接PS,QR,易证PS∥QR,∴P,Q,R,S共面;在C图中分别连接PQ,RS,易证PQ∥RS,∴P,Q,R,S共面;如图所示,在B图中过P,Q,R,S可作一正六边形,故四点共面;D图中PS与QR为异面直线,∴四点不共面,故选ABC.
(1)(多选题)在图中,G,H,M,N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形是( )
(2)如图所示,正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:①直线AM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB1是异面直线;④直线AM与DD1是异面直线.其中正确的结论为______ (注:把你认为正确的结论序号都填上).
[解析] (1)图A中,直线GH∥MN;图B中,G,H,N三点共面,但M∉平面GHN,N∉HG,因此直线GH与MN异面;图C中,连接MG,GM∥HN,因此GH与MN共面;图D中,G,M,N共面,但H∉平面GMN,G∉MN因此GH与MN异面,故选BD.
(2)因为点A在平面CDD1C1外,点M在平面CDD1C1内,直线CC1在平面CDD1C1内,CC1不过点M,所以AM与CC1是异面直线,故①错;取DD1中点E,连接AE,则BN∥AE,但AE与AM相交,故②错;因为B1与BN都在平面BCC1B1内,M在平面BCC1B1外,BN不过点B1,所以BN与MB1是异面直线,故③正确;同理④正确,故填③④.
1.异面直线的判定方法(1)反证法:先假设两条直线不是异面直线,即两条直线平行或相交,由假设出发,经过严格的推理,导出矛盾,从而否定假设,肯定两条直线异面.此法在异面直线的判定中经常用到.(2)判定定理法:平面外一点A与平面内一点B的连线和平面内不经过点B的直线是异面直线.
2.判定平行直线的常用方法(1)三角形中位线的性质.(2)平行四边形的对边平行.(3)平行线分线段成比例定理.(4)公理:若a∥b,b∥c,则a∥c.
〔变式训练2〕(多选题)如图为正方体表面的一种展开图,则在原正方体中,下列说法正确的是( )A.AB与CD是异面直线B.GH与BD相交C.EF∥CDD.EF与GH是异面直线
[解析] 画出该正方体的直观图如图所示,其中异面直线有AB与CD、GH与BD、EF与GH,显然EF∥CD,故选ACD.
(1)(2021·广西玉林模拟)如图,正方体ABCD-A1B1C1D1中,E,F分别为A1B1,CD的中点,则异面直线D1E与A1F所成的角的余弦值为( )
(3)若两条异面直线a、b所成角为60°,则过空间一点O与两异面直线a、b所成角都为60°的直线有______条.[解析] (1)解法一:(平移法)如图,连接BE,BF、D1F,
解法二:(向量法)如图建立空间直角坐标系,不妨设正方体的棱长为2,异面直线D1E与A1F所成角为θ,
注:为便于“平移—作角”常将三棱柱补形成平行六面体,将三棱锥补形成三棱柱(如图)请同学们自己完成解答.
(3)如图,过O分别作a′∥a,b′∥b,则a′,b′所成角为60°,如图易知过O与a′、b′所成角都为60°的直线有3条,即与a,b所成角都为60°的直线有3条.
[引申]本例(3)中与异面直线a、b所成角都为75°的直线有______条.注:与异面直线所成角都为θ,则
求异面直线所成角的方法1.定义法定义法求异面直线所成角的步骤(1)找或作:在图中找或平移异面直线中的一条或两条构造异面直线所成的角.(2)证:说明所作的角是异面直线所成的角.(3)算:寻找或作出含有此角的三角形并解之.(4)取舍:因为异面直线所成角θ的取值范围是0°<θ≤90°,所以所作的角为钝角时,应取它的补角作为异面直线所成的角.
〔变式训练3〕(1)(2022·重庆育才中学诊断)如图所示,已知空间四边形ABCD,AC与BD所成角为60°,且AC=BD=2,E、F分别为BC、AD的中点,则EF=( )
名师讲坛 · 素养提升
(1)若E、F、H分别为正方体ABCD-A1B1C1D1的棱AB、CC1、A1D1的中点,则过E、F、H三点的截面图形是_______________.
[解析] (1)取A1B1的中点M,连EM,连MC1、EF并延长交于Q,作直线HQ交C1D1于N,交B1A1的延长线于S,作直线SE交A1A于P,交B1B的延长线于R,连FR交BC于M,连EM、FN、HP得过E、F、H三点的截面EMFNHP,易证EMFNHP为正六边形.
(1)作截面应遵循的三个原则:①在同一平面上的两点可引直线;②凡是相交的直线都要画出它们的交点;③凡是相交的平面都要画出它们的交线.(2)作交线的方法有如下两种:①利用基本事实3作交线;②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行,然后根据性质作出交线.
注:正六面体的一些截面:说明:正六面体斜截面是不会出现以下几种图形:直角三角形、钝角三角形、直角梯形、正五边形.
〔变式训练4〕(1)(2021·山东枣庄薛城区期中)如图所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥而得到的几何体,现用一个竖直的平面去截这个几何体,则截面图形可能是( )A.(1)(2) B.(1)(3) C.(1)(4) D.(1)(5)
(2)(2022·湖南三湘名校联盟联考)一个正方体内接于一个球,过这个球的球心作一平面,则截面图形不可能是( )
(3)(原创)E、F分别为正方体ABCD-A1B1C1D1的棱CC1、C1D1的中点,则过A、E、F三点的截面的图形是____________.
[解析] (1)当该平面过圆柱上、下底中心时截面图形为(1);当不过上、下底的中心时,截面图形为(5).所以只有(1)(5)正确.故选D.(2)考虑过球心的平面在转动过程中,平面在球的内接正方体上截得的截面不可能是大圆的内接正方形,故选D.
适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量第2节空间点直线平面之间的位置关系课件新人教A版: 这是一份适用于新高考新教材备战2025届高考数学一轮总复习第8章立体几何与空间向量第2节空间点直线平面之间的位置关系课件新人教A版,共47页。PPT课件主要包含了强基础固本增分,研考点精准突破,目录索引,不在一条直线,两个点,有且只有一条,这条直线外,a∩αA,a∥α,a⊂α等内容,欢迎下载使用。
第8章 立体几何与空间向量 第2节 空间点、直线、平面之间的位置关系 2025届高考数学一轮总复习(适用于新高考新教材)ppt: 这是一份第8章 立体几何与空间向量 第2节 空间点、直线、平面之间的位置关系 2025届高考数学一轮总复习(适用于新高考新教材)ppt,共43页。PPT课件主要包含了目录索引,不能写成“⊆”,不在一条直线,两个点,有且只有一条,注意点不在直线上,这条直线外,a∩αA,a∥α,a⊂α等内容,欢迎下载使用。
新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题4立体几何第2讲空间点直线平面之间的位置关系课件: 这是一份新教材适用2024版高考数学二轮总复习第1篇核心专题提升多维突破专题4立体几何第2讲空间点直线平面之间的位置关系课件,共60页。PPT课件主要包含了专题四立体几何,分析考情·明方向,真题研究·悟高考,考点突破·提能力,核心考点3折叠问题等内容,欢迎下载使用。












