2023年陕西省西安市国际港务区铁一中陆港中学中考七模数学试题（含解析）

这是一份2023年陕西省西安市国际港务区铁一中陆港中学中考七模数学试题（含解析），共29页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

2023年陕西省西安市国际港务区铁一中陆港中学中考七模数学试题
学校:___________姓名：___________班级：___________考号：___________

一、单选题
1．实数的算术平方根是（　　）
A． B． C． D．
2．既是轴对称图形又是中心对称图形的是（　　）
A．菱形 B．等边三角形 C．平行四边形 D．扇形
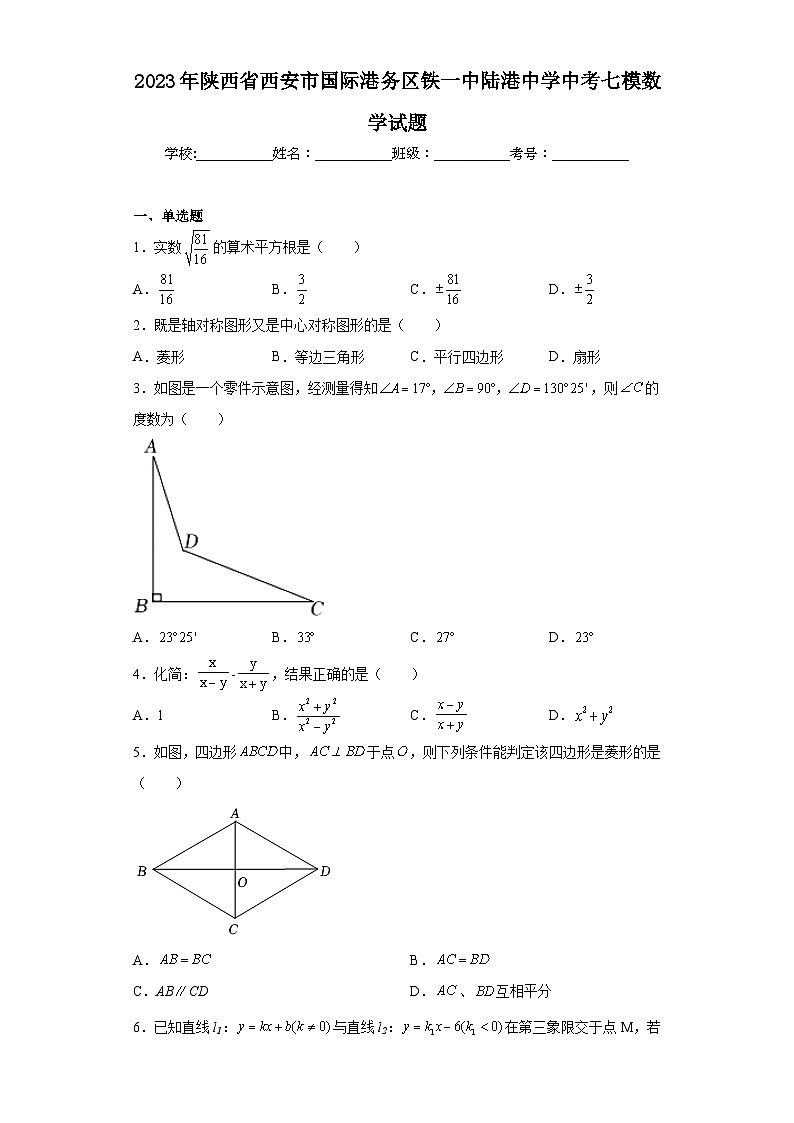
3．如图是一个零件示意图，经测量得知，则的度数为（　　）

A． B． C． D．
4．化简：-，结果正确的是（　　）
A．1 B． C． D．
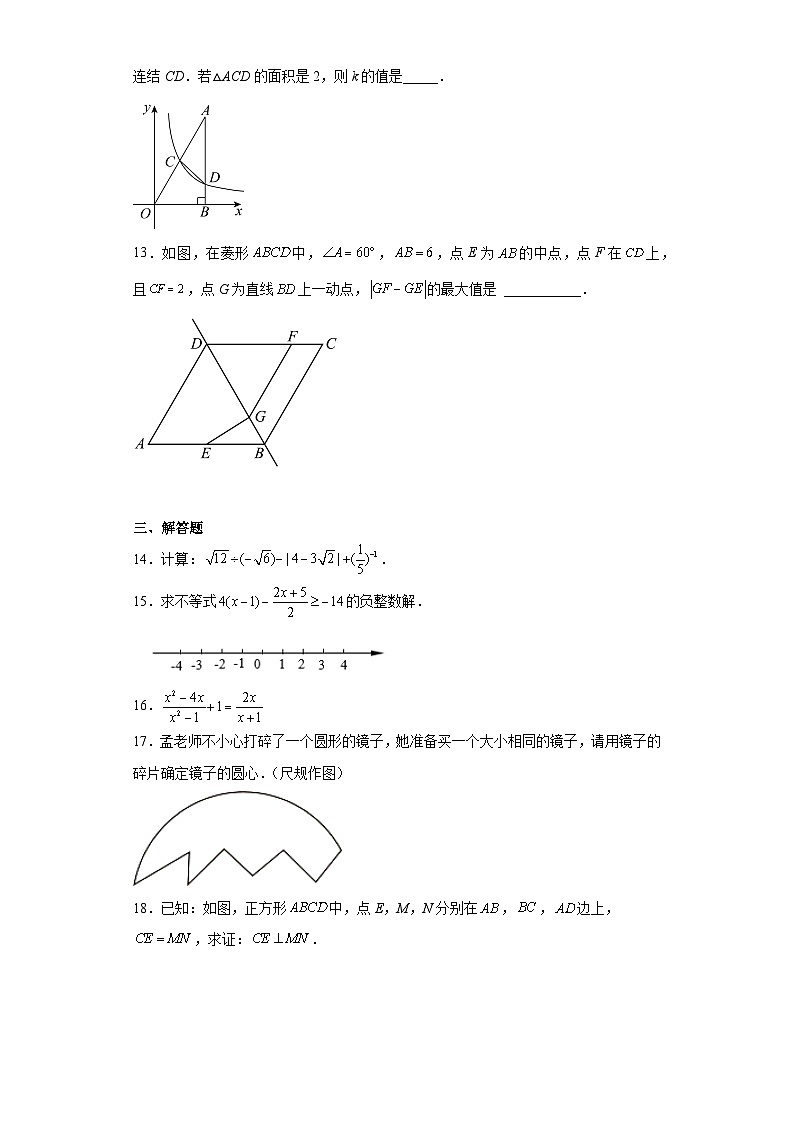
5．如图，四边形中，于点，则下列条件能判定该四边形是菱形的是（ ）

A． B．
C．ABCD D．、互相平分
6．已知直线l1：与直线l2：在第三象限交于点M，若直线l1与x轴的交点为B(3，0)，则k的取值范围是(    )
A． B． C． D．
7．如图，是半径为4的的直径，P是圆上异于A，B的任意一点，的平分线交于点C，连接和，的中位线所在的直线与相交于点E、F，则的长是（　　）

A． B． C．3 D．
8．若一个二次函数的图象经过五个点A（﹣1，n）、B（3，n）、和，则下列关系正确的是（　　）
A． B． C． D．

二、填空题
9．分解因式： =___________．
10．已知中，，是的角平分线，是的外角角平分线，交点为D，则___________．
  
11．已知关于x的不等式组无解，则a的取值范围是_____．
12．如图，已知在平面直角坐标系xOy中，Rt△OAB的直角顶点B在x轴的正半轴上，点A在第一象限，反比例函数y＝（x＞0）的图象经过OA的中点C．交AB于点D，连结CD．若△ACD的面积是2，则k的值是_____．

13．如图，在菱形中，，，点E为的中点，点F在上，且，点G为直线上一动点，的最大值是 ___________．
  

三、解答题
14．计算：．
15．求不等式的负整数解．

16．
17．孟老师不小心打碎了一个圆形的镜子，她准备买一个大小相同的镜子，请用镜子的碎片确定镜子的圆心．（尺规作图）

18．已知：如图，正方形中，点E，M，N分别在，，边上，，求证：．

19．疫情期间为保护学生和教师的健康，某学校储备“抗疫物资”，用19000元购进甲、乙两种医用口罩共计900盒，甲、乙两种口罩的售价分别是20元/盒，25元/盒．
(1)求甲、乙两种口罩各购进了多少盒？
(2)现已知甲、乙两种口罩的数量分别是20个/盒，25个/盒，按照市教育局要求，学校必须储备足够使用10天的口罩，该校师生共计900人，每人每天2个口罩，问购买的口罩数量是否能满足市教育局的要求？
20．“石头、剪子、布”是一个广为流传的游戏，规则是：甲、乙两人都做出“石头”“剪子”“布”3种手势中的1种，其中“石头”赢“剪子”，“剪子”赢“布”，“布”赢“石头”，手势相同不分输赢．假设甲、乙两人每次都随意并且同时做出3种手势中的1种．
(1)甲每次做出“石头”手势的概率为_________；
(2)用画树状图或列表的方法，求乙不输的概率．
21．如图是某种云梯车的示意图，云梯升起时，与底盘夹角为，液压杆与底盘夹角为．已知液压杆，当，时，求的长．

22．2022年北京冬奥会圆满结束，中国健儿奋力拼搏，一共获得了9枚金牌、4枚银牌、2枚铜牌．校学生会在全校范围内随机地对本校一些学生进行了“我最喜欢的冬奥会运动健儿”问卷调查（问卷共设有五个选项：“A-武大靖”、“B-徐梦桃”、“C-谷爱凌”、“D-苏翊鸣”、“E-齐广璞”，参加问卷调查的这些学生，每人都只选了其中的一个选项），将所有的调查结果绘制成如下两幅不完整的统计图：

请你根据以上信息，回答下列问题：
(1)此次调查的样本容量是___________；在扇形统计图中，选项“A-武大靖”所在扇形的圆心角度数是___________；
(2)补全上面的条形统计图；
(3)该校共有3000名学生，请你估计该校学生“最喜欢的冬奥会运动健儿”为“E-齐广璞”的人数．
23．如图，在直角坐标系中，直线与反比例函数的图象交于A、B两点，已知A点的纵坐标是2，

(1)求反比例函数的表达式；
(2)根据图象求的解集；
(3)将直线向上平移后与y轴交于点C，与双曲线在第二象限内的部分交于点D，如果△ABD的面积为36，求平移后的直线表达式．
24．如图，是的直径，点C为上一点，的外角平分线交于点D，是切线，交的延长线于点E，连接．

(1)求证：；
(2)若，，求的长．
25．如图，在平面直角坐标系中，二次函数y＝﹣x2+bx+c的图象与x轴交于A、B两点，与y轴交于C（0，3），A点在原点的左侧，B点的坐标为（3，0）．点P是抛物线上一个动点，且在直线BC的上方．
（1）求这个二次函数的表达式．
（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形 ABPC的面积最大，并求出此时点P的坐标和四边形ABPC的最大面积．

26．问题提出：
（1）如图①，若，，，则的面积为 ___________；
问题发现：
（2）如图②，在四边形中，，，，，点M，N分别为边，上两动点，且，连接，，试说明四边形的面积是定值；
问题解决：
（3）如图③是一块平行四边形空地，其中，，，点M，N分别为边上两点，且，连接．公司规划在区域修建一座购物商城，在区域修建一个顾客休息中心，在区修建小吃城，最后中间区域进行绿化．公司为了利益最大化，绿化面积即的面积尽可能小．请你计算出绿化面积的最小值和的长度．


参考答案：
1．B
【分析】一般地，如果一个正数的平方等于，即，那么这个正数x叫做a的算术平方根．记为，由此即可求解．
【详解】解：∵，
∴的算术平方根是．
故选：B．
【点睛】本题考查算术平方根，关键是掌握算术平方根的定义．
2．A
【分析】根据轴对称图形与中心对称图形的概念求解．
【详解】解：A、菱形轴对称图形，也是中心对称图形，符合题意；
B、等边三角形是轴对称图形，不是中心对称图形，不符合题意；
C、平行四边形是中心对称图形，不是轴对称图形，不符合题意；
D、扇形是轴对称图形，不是中心对称图形，不符合题意．
故选：A．
【点睛】本题考查中心对称图形和轴对称图形的知识，关键是掌握好中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180度后与原图重合．
3．A
【分析】连接，并延长至点E，利用三角形的外角性质，可得出，进而可得出，再代入各角的度数，即可求出的度数．
【详解】解：连接，并延长至点E，如图所示．

∵是的外角，是的外角，
∴，
∴
，
即，
∴．
故选：A．
【点睛】本题考查了三角形的外角性质，牢记“三角形的一个外角等于和它不相邻的两个内角的和”是解题的关键．
4．B
【分析】先将分母进行通分，化为（x+y）（x-y）的形式，分子乘上相应的分式，进行化简.
【详解】
【点睛】本题考查的是分式的混合运算，解题的关键就是熟练掌握运算规则.
5．D
【分析】先证四边形是平行四边形，再由菱形的判定定理即可得出结论．
【详解】解：能判定该四边形是菱形的是、互相平分，理由如下：
、互相平分，
四边形是平行四边形，
又，
平行四边形是菱形，
故选：D．
【点睛】本题考查了菱形的判定、平行四边形的判定与性质等知识，熟练掌握菱形的判定和平行四边形的判定是解题的关键．
6．D
【分析】由题意易得直线l2经过二、三、四象限，画出大致图像如图所示，要使交点M在第三象限，直线l1可绕B点旋转，找到两个极限位置，即可得到k的取值范围.
【详解】根据题意画出大致图像，如图所示，当l1经过（0，-6）时，将（3,0）和（0，-6）代入得，，解得，此时直线l1解析式为，
此时直线l1绕B点顺时针旋转至与x轴重合的过程中，交点M始终在第三象限，所以k的取值范围是，故选D.

【点睛】本题考查一次函数的交点问题，采用数形结合，画出草图是解题的关键.
7．A
【分析】连接、，交于D，由圆周角定理得出，根据垂径定理可知：必垂直平分．由是的中位线，根据三角形中位线定理可得：．在中求出的长，即可得出的值．
【详解】解：如图所示，
∵是的角平分线，
∴，
∴，
∴，
∵是直径，
∴，
即是等腰直角三角形．
连接，交于点D，则，
∵是的中位线，
∴，
∴，，
∴，
连接，根据勾股定理，得：，
∴．
故选：A．

【点睛】此题考查圆周角定理，垂径定理，三角形的中位线，综合运用了圆周角定理及其推论发现等腰直角三角形，再进一步根据等腰三角形的性质以及中位线定理，求得的弦心距，最后结合垂径定理和勾股定理求得弦长．
8．B
【分析】先求出二次函数的对称轴为直线，再由，可得二次函数的图象上的点里对称轴越远，函数值越大，即可求解．
【详解】解：∵二次函数的图象经过点A（﹣1，n）、B（3，n），
∴二次函数的对称轴为直线，
∵，
∴二次函数的图象上的点里对称轴越远，函数值越大，
∵，
∴．
故选：B
【点睛】本题主要考查了二次函数的图象和性质，根据题意得到二次函数的对称轴为直线是解题的关键．
9．
【分析】先提取公因式，再用公式法计算即可．
【详解】解：

，
故答案为：．
【点睛】本题考查了提公因式法与公式法的综合，熟练掌握因式分解的方法是解题的关键．
10．
【分析】由角平分线的定义可得，，再由三角形的外角性质可得，，从而可求解．
【详解】解：∵是的角平分线，是的外角角平分线，
∴，，
∵是的外角，是的外角，
∴，，
∴


．
故答案为：．
【点睛】本题主要考查三角形的外角性质，解答的关键是熟记三角形的外角性质：三角形的外角等于与其不相邻的两个内角之和．
11．a≥2
【分析】先把a当作已知条件求出各不等式的解集，再根据不等式组无解求出a的取值范围即可．
【详解】解：，
由①得：x≤2，
由②得：x＞a，
∵不等式组无解，
∴a≥2，
故答案为a≥2．
【点睛】本题主要考查了解一元一次不等式组，解题的关键关键是掌握解集的规律：同大取大；同小取小；大小小大中间找；大大小小无处找．
12．
【分析】作辅助线，构建直角三角形，利用反比例函数k的几何意义得到S△OCE=S△OBD=k，根据OA的中点C，利用△OCE∽△OAB得到面积比为1：4，代入可得结论．
【详解】解：连接OD，过C作CE∥AB，交x轴于E，

∵∠ABO＝90°，反比例函数y＝（x＞0）的图象经过OA的中点C，
∴S△COE＝S△BOD＝，S△ACD＝S△OCD＝2，
∵CE∥AB，
∴△OCE∽△OAB，
∴，
∴4S△OCE＝S△OAB，
∴4×k＝2+2+k，
∴k＝，
故答案为：．
【点睛】本题考查了反比例函数比例系数k的几何意义：在反比例函数y=图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．在反比例函数的图象上任意一点向坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是|k|，且保持不变．也考查了相似三角形的判定与性质．
13．
【分析】取的中点，连接，，过点作于H点．解直角三角形求出，根据可得结论．
【详解】解：取的中点，连接，，过点作于H点．
  
∵四边形是菱形，，，
∴，，
∵点E为的中点，点为的中点，
∴，，
∵四边形是菱形，，且，，
∴点E与点关于对称，
∴，
∵，，
∴，，
∴，
∴在中，，
∵，当且仅当F、G、三点共线时取等号，
∴，
∴的最大值为．
故答案为：．
【点睛】本题考查轴对称﹣最短问题，解直角三角形，勾股定理以及菱形的性质等知识，解题的关键是学会利用轴对称解决最值问题，属于中考常考题型．
14．
【分析】先计算二次根式的除法、去绝对值、负整数指数幂，再进行加减运算即可．
【详解】


．
【点睛】本题考查二次根式的混合运算．涉及二次根式的除法、去绝对值和负整数指数幂．掌握二次根式的混合运算法则是解题关键．
15．-2、-1；
【分析】解不等式求出解集，则可得出答案．
【详解】解：去分母得：，
去括号得：，
移项得：，
合并同类项得：，
系数化为1得：，
所以，原不等式组的解集是 ，
负整数解是 -2、-1．
【点睛】本题主要考查根据不等式性质求不等式的解集，根据不等式解集情况找出符合的整数解．
16．
【详解】试题分析：首先在方程的两边同时乘以(x+1)(x-1)，将分式方程转化为整式方程，求出方程的解，对于分式方程最后必须要进行验根.
试题解析：在方程左右两边同时乘以(x+1)(x-1)可得：
化简整理可得：2x=-1      解得：x=
经检验：x=是原方程的解.
17．见解析
【分析】在圆弧上取A，B，C三点，连接，，作线段，的垂直平分线交于点O，点O即为所求．
【详解】解：如图，点O即为所求．

【点睛】本题考查作图﹣应用与设计作图，线段的垂直平分线的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
18．见解析
【分析】作于F，先根据证明，得出对应角相等，再根据角的互余关系，即可得出结论．
【详解】证明：作于F，如图所示：

则，四边形是矩形，
∴，
∵四边形是正方形，
∴，，
∴，
在和中，，
∴，
∴，
∵，
∴，
∴，
∴．
【点睛】本题考查了正方形的性质以及全等三角形的判定与性质；通过作辅助线构造三角形全等是解决问题的关键．
19．(1)甲种口罩购进了700盒，乙种口罩购进了200盒
(2)购买的口罩数量能满足市教育局的要求

【分析】（1）设甲种口罩购进了x盒，乙种口罩购进了y盒，根据总价=单价×数量，结合用19000元购进甲、乙两种医用口罩共计900盒，即可得出关于x，y的二元一次方程组，解之即可得出甲、乙两种口罩购进数量；
（2）利用购进口罩的总数量=每盒的个数×购进数量，可求出购进口罩的总数量，利用市教育局的要求数=2×该校师生人数×10，可求出学校需要口罩的总数量，比较后即可得出购买的口罩数量能满足市教育局的要求．
【详解】（1）解：设甲种口罩购进了x盒，乙种口罩购进了y盒，
依题意得：，
解得：．
答：甲种口罩购进了700盒，乙种口罩购进了200盒；
（2）解：20×700+25×200=14000+5000=19000（个），
2×900×10=18000（个）．
∵19000＞18000，
∴购买的口罩数量能满足市教育局的要求．
【点睛】本题考查了二元一次方程组的应用以及有理数的混合运算，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）利用购进口罩的总数量=每盒的个数×购进数量，求出购进口罩的总数量．
20．(1)
(2)见解析，

【分析】（1）根据概率计算公式求解即可；
（2）先画树状图得出所有的等可能性的结果数，然后找到乙不输的结果数，最后利用概率计算公式求解即可．
【详解】（1）解：∵甲每次做出的手势只有“石头”、“剪子”、“布”其中的一种，
∴甲每次做出“石头”手势的概率为；
（2）解：树状图如图所示：

甲、乙两人同时做出手势共有9种等可能结果，其中乙不输的共有6种，
∴（乙不输）．
答：乙不输的概率是．
【点睛】本题主要考查了简单的概率计算，利用列表法或树状图法求解概率，熟知概率计算公式是解题的关键．
21．
【分析】利用锐角三角函数可求，的长，即可求解，结合图形求得的长度．
【详解】解：，
，
．
，
，
，
，
，
．
．
【点睛】本题考查了解直角三角形的应用，熟练运用锐角三角函数求线段的长是解题的关键．
22．(1)300，
(2)见解析
(3)150人

【分析】（1）利用频数÷百分比求出总数，利用百分比求出圆心角的度数；
（2）利用总数×百分比求出选项的人数，再补全即可；
（3）利用总体×样本中喜欢“E-齐广璞”的学生所占的比重，即可得解．
【详解】（1）此次调查的样本容量为：；
选项“A-武大靖”所在扇形的圆心角度数是：；
故答案为：300，；
（2）选项的人数为：人，
补全条形统计图为：

（3）根据题意得：
人，
所以估计该校学生“最喜欢的冬奥会运动健儿”为“E-齐广璞”的人数为150人．
【点睛】本题考查扇形图和条形图的综合应用．通过统计图，有效的获取信息，利用频数＝总数×百分比，圆心角度数＝百分比，进行计算，是解题的关键．
23．(1)y＝﹣；
(2)﹣6＜x＜0或x＞6；
(3)y＝﹣x+6

【分析】（1）利用y＝﹣x求出点A的坐标为（﹣6，2），将点A（﹣6，2）代入反比例函数中求出k即可；
（2）根据对称性得到点B的横坐标为6，再结合图象即可得到解集；
（3）连接AC、BC，设平移后的解析式为y＝﹣x+b，根据平移的性质得到S△ABD＝S△ABC，列得b×12＝36，求出b即可得到函数解析式．
【详解】（1）解：（1）令一次函数y＝﹣x中y＝2，则2＝﹣x，
解得：x＝﹣6，即点A的坐标为（﹣6，2），
∵点A（﹣6，2）在反比例函数的图象上，
∴k＝﹣6×2＝﹣12，
∴反比例函数的表达式为y＝﹣；
（2）由对称性可知：x＝﹣x，
∵x＝﹣6，
∴x＝6，
由图象可知，﹣x＜的解集为﹣6＜x＜0或x＞6；
（3）连接AC、BC如图所示．

设平移后的解析式为y＝﹣x+b，
∵该直线平行直线AB，
∴S△ABD＝S△ABC，
∵△ABD的面积为36，
∴S△ABC＝OC•（x﹣x）＝36，
∴b×12＝36，
∴b＝6，
∴平移后的直线的函数表达式为y＝﹣x+6．
【点睛】本题考查了反比例函数与一次函数交点的问题、反比例函数图象上点的坐标特征，三角形面积，数形结合是解题的关键．
24．(1)见解析
(2)12

【分析】（1）连接，根据切线性质可得，再利用角平分线和等腰三角形可证，从而利用平行线的性质可得，然后利用直径所对的圆周角是直角可得，从而利用平行线的判定即可解答；
（2）过点作，垂足为F，根据垂径定理可得，，再利用（1）的结论可得四边形是矩形，从而可得，然后根据直径所对的圆周角是直角可得，从而证明，进而利用相似三角形的性质进行计算求出，最后求出，的长，从而求出的长，即可解答．
【详解】（1）证明：连接，

∵与相切于点D，
∴，
∵平分，
∴，
∵，
∴，
∴，
∴，
∴，
∵是的直径，
∴，
∴，
∴；
（2）解：过点O作，垂足为F，

∴，，
∵，
∴四边形是矩形，
∴，
∵是的直径，
∴，
∵，，
∴，
∴，
∴，
∴，
∴，
∴，
∴，
∴的长为．
【点睛】本题考查了切线的性质，圆周角定理，相似三角形的判定与性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
25．（1）y＝﹣x2+2x+3；（2）P点的坐标为；（3）P点的坐标为，四边形ABPC面积的最大值为．
【分析】（1）根据待定系数法，可得函数解析式；（2）根据菱形的对角线互相平分，可得P点的纵坐标，根据函数值与自变量的对应关系，可得答案；（3）根据面积的和差，可得二次函数，根据二次函数的性质，可得m的值，根据自变量与函数值的对应关系，可得P点坐标．
【详解】解：（1）将B、C两点的坐标代入得 ，
解得．
所以二次函数的表达式为y＝﹣x2+2x+3；
（2）如图，
，
存在点P，使四边形POP′C为菱形．
设P点坐标为（x，﹣x2+2x+3），
PP′交CO于E
若四边形POPC是菱形，则有PC＝PO．
连接PP则PE⊥CO于E．
∴OE＝CE＝，
∴y＝．
∴﹣x2+2x+3=，
解得x1＝，x2＝（不合题意，舍去）
∴P点的坐标为．
（3）如图1，
，
过点P作y轴的平行线与BC交于点Q，与OB交于点F，设P（x，﹣x2+2x+3）
易得，直线BC的解析式为y＝﹣x+3．
则Q点的坐标为（x，﹣x+3）．
PQ＝﹣x2+3x．
S四边形ABPC＝S△ABC+S△BPQ+S△CPQ＝AB•OC+QP•BF+QP•OF
＝×4×3+（﹣x2+3x）×3
＝﹣（x﹣）2+，
当x=时，四边形ABPC的面积最大
此时P点的坐标为，四边形ABPC面积的最大值为．
【点睛】本题考查了二次函数综合题，利用待定系数法求函数解析式；利用菱形的性质得出P点的纵坐标是解题关键；利用面积的和差得出二次函数是解题关键．
26．（1）；（2）见解析；（3），200m
【分析】（1）过点C作于D，根据勾股定理计算高的长，由三角形面积公式可得结论；
（2）连接，过点A作交的延长线于点E，过点A作交的延长线于点F，设，通过证明可得，则，根据30度角的正切列方程可得x的值，根据面积和表示四边形的面积，即可得结果；
（3）作辅助线，过点作的垂线段，交的延长线于点P，过点A作的垂线段，交的延长线于点Q，过点N作于E，设，利用面积差表示，利用二次函数性质即可得结论．
【详解】（1）解：如图1，过点C作于D，

，
，

，
，
的面积，
故答案为：；
（2）解：如图2，连接，过点A作交的延长线于点E，过点A作交的延长线于点F，则，

在与中，
，
，
∴，，，
，
，
，，
是等腰直角三角形，
，
设，则，  
∴，
解得，
∴，

，
故四边形的面积为，
∴四边形的面积是定值；
（3）如图3，过点A作交的延长线于点Q，过点A作交的延长线于点P，过点N作于E，则，

设，则，，
∵四边形是平行四边形，
∴，，，
，，
，，
在中， ，即，
，
在中， ，即，
，
在中，，，
，
可得平行四边形的面积为，
，
，
，
，

，
∴当时，的面积最小，其最小值是，即绿化面积的最小值。
【点睛】本题是四边形综合题，涉及到勾股定理，直角三角形的性质，锐角三角函数，二次函数的性质，三角形和平行四边形的面积等，解题关键是利用函数判断最小值．