解析版·湖北省黄冈市2017届高三上学期期末考试数学理试题 Word版

湖北省黄冈市2017届高三上学期期末考试

数学理试题

第Ⅰ卷（选择题）

一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.

1.设复数，其中i是虚数单位，则的模为

A.      B.     C.     D. 1

【答案】D

【解析】

试题分析：因为，所以；故选D．1

考点：复数的概念．

2.下列说法正确的是

  A. “若，则”的否命题是“若，则”   

 B.  在中，“” 是“”必要不充分条件

 C. “若，则”是真命题   

D.使得成立

【答案】C

考点：1.四种命题；2.充分条件和必要条件．

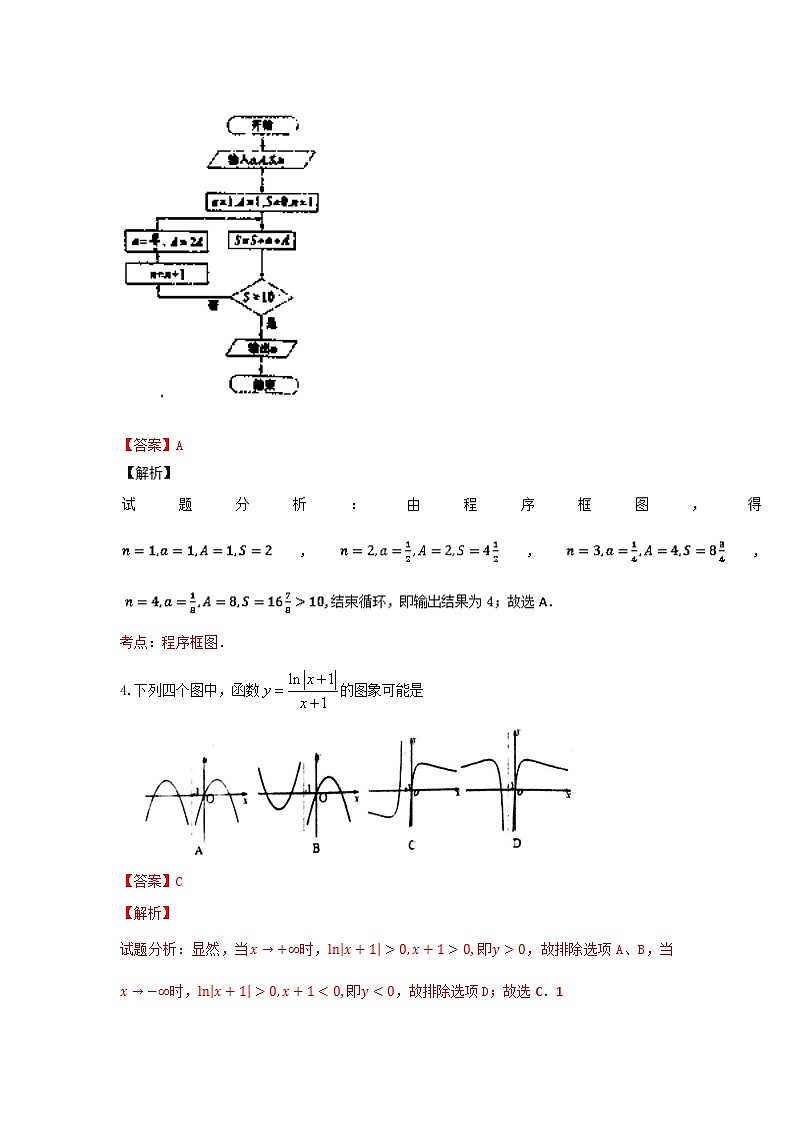
3.我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题：“今有堩厚十尺，两鼠对穿，初日各一尺，大鼠日自倍，小鼠日自半，问几何日相逢？”现有程序框图描述，如图所示，则输出结果

  A.  4    B. 5    C.  2   D.  3

【答案】A

考点：程序框图．

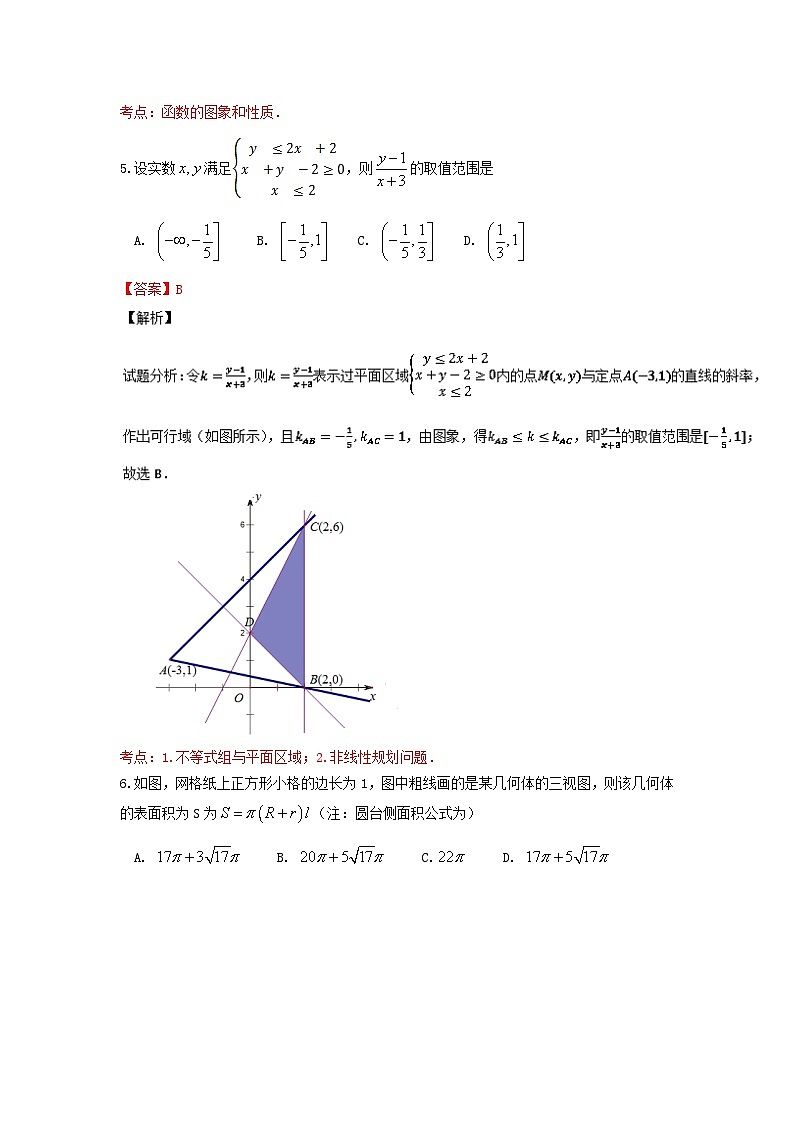
4.下列四个图中，函数的图象可能是

【答案】C

【解析】

试题分析：显然，当时，,即，故排除选项A、B，当时，,即，故排除选项D；故选C．1

考点：函数的图象和性质．

5.设实数满足，则的取值范围是

  A.      B.     C.     D.

【答案】B111.Com]

考点：1.不等式组与平面区域；2.非线性规划问题．

6.如图，网格纸上正方形小格的边长为1，图中粗线画的是某几何体的三视图，则该几何体的表面积为S为（注：圆台侧面积公式为）

  A.      B.      C.     D.

【答案】D

【解析】1111]

试题分析：由三视图可知，该几何体是由一个半球和一个圆台（上底面与球的大圆面重合）组成，其中半球的半径为2，其曲面面积为，圆台的底面半径分别为2,3，高为4，母线长为，则侧面积为，下底面的面积为，则该几何体的表面积为；故选D．1

考点：1.三视图；2.几何体的表面积．

7.已知的外接圆的圆心为O，半径为2，且，则向量在向量方向上的投影为

  A.      B.     C.     D.

【答案】B

考点：1.平面向量的线性运算；2.平面向量的数量积运算．

8.在正三棱柱中，若，则与所成角的大小为

  A.      B.     C.     D.

【答案】D

【解析】

试题分析：不妨设，则，即直线与所成的角为；故选D．

考点：1.异面直线所成的角；2.平面向量的数量积．

9.已知函数的图象关于直线对称，则

  A.      B.     C.     D.

【答案】D

考点：1.配角公式；2.三角函数的图象与性质．

10.已知函数是定义在上的偶函数,为奇函数，,当时，，则在区间内满足方程的实数为

  A.      B.     C.     D.

【答案】B

【解析】

试题分析：因为函数是定义在上的偶函数,为奇函数，所以函数既关于直线对称，也关于直线对称，则函数是以为周期的周期函数，由题意，将化为，即，解得；故选B．1

考点：1.函数的性质；2.对数式的运算．

11.如图，给定由10个点（任意相邻两点距离为1）组成的正三角形点阵，在其中任意取三个点，以这三个点为顶点构成的正三角形的个数是111]

  A. 12     B. 13    C. 15    D. 16

【答案】C

【解析】

试题分析：由题意得，边长为1的正三角形共有个，边长为2的正三角形共有3个，边长为3的正三角形共有1个，边长为的正三角形共有2个，综上，共有个正三角形；故选C．

考点：归纳推理．1

12.已知函数在处取得最大值，以下各式中：①②③④⑤

正确的序号是

  A. ②④     B. ②⑤    C. ①④    D. ③⑤

【答案】A

，所以在左侧，所以，所以，所以，所以，即④正确；故选A．

考点：导数在研究函数中的应用．

第Ⅱ卷（非选择题）

二、填空题：本大题共4小题，每小题5分，共20分.

13.设函数，则满足的取值范围为                .

【答案】

考点：1.分段函数；2.一元二次不等式．

14.多项式的展开式中的系数为                .（用数字作答）

【答案】-6480

【解析】

试题分析：由二项式定理得，多项式的展开式中的系数为；故填-6480．1

考点：二项式定理．

15.有一个电动玩具，它有一个的长方形（单位：cm）和一个半径为1cm的小圆盘（盘中娃娃脸），他们的连接点为A,E,打开电源，小圆盘沿着长方形内壁，从点A出发不停地滚动（无滑动），如图所示，若此时某人向该长方形盘投掷一枚飞镖，则能射中小圆盘运行区域内的概率为                .

【答案】

【解析】

试题分析：由题意得，四个角空的面积为，滚动矩形区域的面积为，则滚动区域面积为，由几何概型的概率公式，得某人向该长方形盘投掷一枚飞镖，则能射中小圆盘运行区域内的概率为；故填．

考点：几何概型．

16.设数列满足，且，若表示不超过的最大整数，则                .

【答案】2016

考点：1.数列的递推式与通项；2.裂项抵消法．

三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或推理、验算过程.

17.（本题满分10分）

已知函数

   （1）若关于的方程只有一个实数解，求实数a的取值范围；

   （2）若当时，不等式恒成立，求实数a的取值范围.

【答案】(1)；(2)．

【解析】

试题分析：(1)利用平方差公式，将等式变形，转化为的解的个数问题进行求解；(2)分离参数，将不等式恒成立问题转化为求函数的最值问题，再分离参数时，要注意对和1的大小关系进行讨论．

试题解析：（Ⅰ）方程|f（x）|=g（x），即|x2﹣1|=a|x﹣1|，变形得|x﹣1|（|x+1|﹣a）=0，显然，x=1已是该方程的根，从而欲使原方程只有一解，即要求方程|x+1|=a有且仅有一个等于1的解或无解，∴a＜0．…………5分

（Ⅱ）当x∈R时，不等式f（x）≥g（x）恒成立，即（x2﹣1）≥a|x﹣1|（*）对x∈R恒成立，

①当x=1时，（*）显然成立，此时a∈R；

②当x≠1时，（*）可变形为a≤，

令φ（x）==1111]

因为当x＞1时，φ（x）＞2，当x＜1时，φ（x）＞﹣2，所以φ（x）＞﹣2，故此时a≤﹣2．

综合①②，得所求实数a的取值范围是a≤﹣2．…………10分

考点：1.绝对值不等式；2.分类讨论思想的应用．

18.（本题满分12分）

   函数的部分图像如图所示，将的图象向右平移个单位长度后得到函数的图象.

   （1）求函数的解析式；

   （2）在中，角A,B,C满足，且其外接圆的半径R=2，求的面积的最大值.

【答案】(1)；(2)．

（Ⅱ）∵

∴

∵

，即，所以或1（舍），……8分

由正弦定理得，解得

由余弦定理得

∴，（当且仅当a=b等号成立）

∴

∴的面积最大值为.……………………12分

考点：1.三角函数的图象与性质；2.三角函数的图象变换；3.正弦定理与余弦定理；4.基本不等式．1111]

19.（本题满分12分）

    已知数列的前项和，n为正整数.

   （1）令，求证：数列为等差数列，并求出数列的通项公式；

   （2）令，求.

【答案】(1)证明略，；(2)．

考点：1.和的关系的应用；2.等比数列；3.错位相减法．

20.（本题满分12分）为了引导居民合理用水，某市决定全面实施阶梯水价，阶梯水价原则上以住宅（一套住宅为一户）的月用水量为基准定价，具体划分标准如下表：

从本市随机抽取了10户家庭，统计了同一个月的用水量，得到右边的茎叶图：  

（1）现要在这10户家庭中任意选取3户，求取到第二阶梯水量的户数的分布列和数学期望；

（2）用抽到的10户家庭作为样本估计全市的居民用水情况，从全市依次随机抽取10户，若抽到n户月用水用量为第二阶梯水量的可能性最大，求出n的值.

【答案】(1)分布列略，；(2)6．

设    …………………10分

若，则，；

若，则，。

所以当或，可能最大，

所以的取值为6。………………12分

考点：1.茎叶图；2.抽样方法；离散型随机变量的分布列和数学期望；4.二项分布．

21.（本题满分12分）如图，在各棱长均为2的三棱柱中，侧面底面，

  （1）求侧棱与平面所成角的正弦值的大小；

   （2）已知点D满足，在直线上是否存在点P,使DP//平面？若存在，请确定点P的位置，若不存在，请说明理由.

【答案】(1)；(2)．

又，且各棱长都相等，

∴，，．…2分

故以为坐标原点，建立如图所示的空间直角坐标系，则

，，，，

∴，，．……4分

设平面的法向量为，

则 ,解得．由．   

而侧棱与平面所成角，即是向量与平面的法向量所成锐角的余角，

∴侧棱与平面所成角的正弦值的大小为…………………6分

（2）∵，而

∴又∵，∴点的坐标为．                     

假设存在点符合题意，则点的坐标可设为，∴．

∵，为平面的法向量，

∴由，得．                  ……………10分

又平面，故存在点，使，其坐标为，

即恰好为点．………12分

考点：1.空间中线面垂直关系的转化；2.空间向量在立体几何中的应用．

22.（本题满分12分）已知函数在定义域内有两个不同的极值点.

   （1）求实数a的取值范围；

   （2）记两个极值点为，且，已知，若不等式恒成立，求的取值范围.

【答案】(1)；(2)．

（解法三）令g（x）=lnx﹣ax，从而转化为函数g（x）有两个不同零点，
而（x＞0），
若a≤0，可见g′（x）＞0在（0，+∞）上恒成立，所以g（x）在（0，+∞）单调增，
此时g（x）不可能有两个不同零点．
若a＞0，在时，g′（x）＞0，在时，g′（x）＜0，
所以g（x）在上单调增，在上单调减，从而=，
又因为在x→0时，g（x）→﹣∞，在在x→+∞时，g（x）→﹣∞，
于是只须：g（x）极大＞0，即，所以．
综上所述，． ……4分

（Ⅱ）因为等价于1+λ＜lnx1+λlnx2．
由（Ⅰ）可知x1，x2分别是方程lnx﹣ax=0的两个根，
即lnx1=ax1，lnx2=ax2
所以原式等价于1+λ＜ax1+λax2=a（x1+λx2），因为λ＞0，0＜x1＜x2，
考点：1.导数在研究函数中的应用；2.导数在研究不等式中的应用．