2021北京十三中初三（上）期中数学（教师版）

2021北京十三中初三（上）期中

数    学

一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个。

1．（2分）围棋起源于中国，古代称之为“弈”，至今已有4000多年的历史．2017年5月，世界围棋冠军柯洁与人工智能机器人AlphaGo进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（　　）

A． B． 

C． D．

2．（2分）函数y＝（x+1）2﹣2的最小值是（　　）

A．1 B．﹣1 C．2 D．﹣2

3．（2分）若关于x的方程ax2﹣2ax+1＝0的一个根是﹣1，则a的值是（　　）

A．1 B．﹣1 C．﹣ D．﹣3

4．（2分）下列方程中，无实数根的方程是（　　）

A．x2+3x＝0 B．x2+2x﹣1＝0 C．x2+2x+1＝0 D．x2﹣x+3＝0

5．（2分）直径为10分米的圆柱形排水管，截面如图所示．若管内有积水（阴影部分），水面宽AB为8分米，则积水的最大深度CD为（　　）

A．2分米 B．3分米 C．4分米 D．5分米

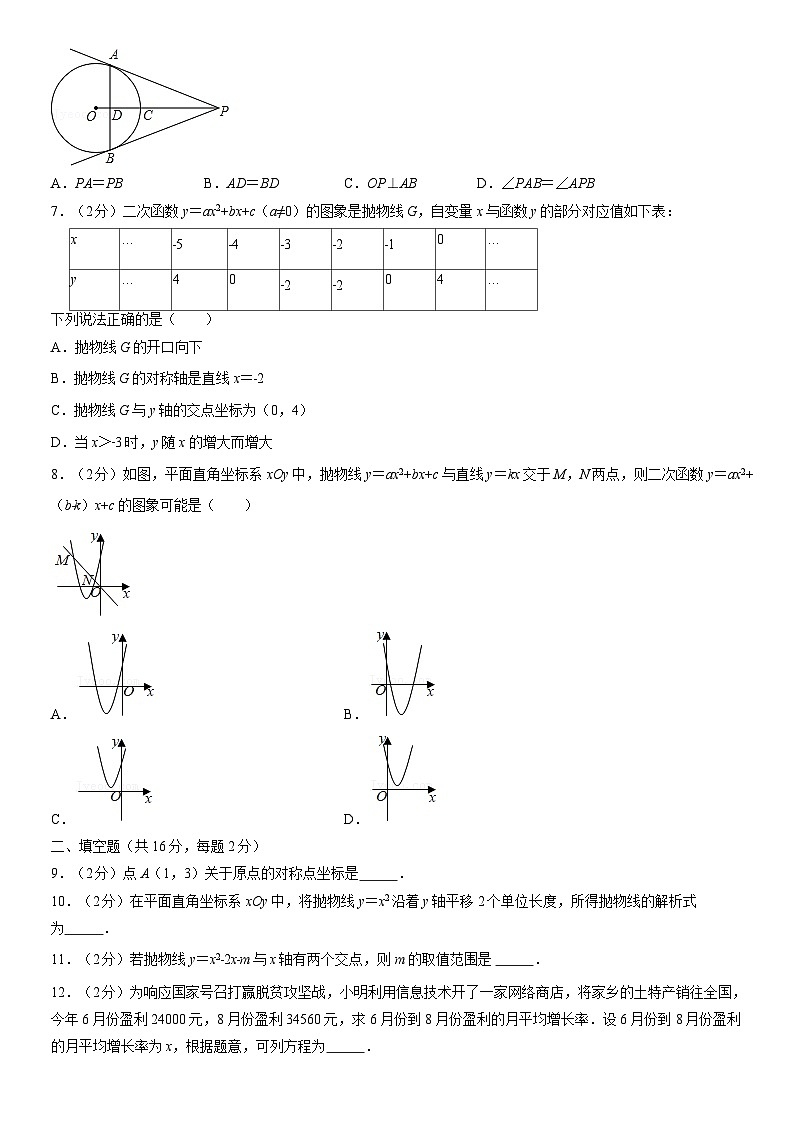
6．（2分）如图，PA，PB为⊙O的两条切线，点A，B是切点，OP交⊙O于点C，交弦AB于点D．下列结论中错误的是（　　）

A．PA＝PB B．AD＝BD C．OP⊥AB D．∠PAB＝∠APB

7．（2分）二次函数y＝ax2+bx+c（a≠0）的图象是抛物线G，自变量x与函数y的部分对应值如下表：

下列说法正确的是（　　）

A．抛物线G的开口向下 

B．抛物线G的对称轴是直线x＝﹣2 

C．抛物线G与y轴的交点坐标为（0，4） 

D．当x＞﹣3时，y随x的增大而增大

8．（2分）如图，平面直角坐标系xOy中，抛物线y＝ax2+bx+c与直线y＝kx交于M，N两点，则二次函数y＝ax2+（b﹣k）x+c的图象可能是（　　）

A． B． 

C． D．

二、填空题（共16分，每题2分）

9．（2分）点A（1，3）关于原点的对称点坐标是　   　．

10．（2分）在平面直角坐标系xOy中，将抛物线y＝x2沿着y轴平移2个单位长度，所得抛物线的解析式为　   　．

11．（2分）若抛物线y＝x2﹣2x﹣m与x轴有两个交点，则m的取值范围是 　   　．

12．（2分）为响应国家号召打赢脱贫攻坚战，小明利用信息技术开了一家网络商店，将家乡的土特产销往全国，今年6月份盈利24000元，8月份盈利34560元，求6月份到8月份盈利的月平均增长率．设6月份到8月份盈利的月平均增长率为x，根据题意，可列方程为　   　．

13．（2分）如图所示的正方形网格中，A，B，C，D，P是网格线交点．若∠APB＝α，则∠BPC的度数为　   　（用含α的式子表示）．

14．（2分）如图，正方形ABCD内接于⊙O，点E在上，则∠BEC＝　   　度．

15．（2分）如图，△ABC为等腰三角形，O是底边BC的中点，若腰AB与⊙O相切，则AC与⊙O的位置关系为　   　（填“相交”、“相切”或“相离”）．

16．（2分）如图1，在△ABC中，AB＞AC，D是边BC上一动点，设B，D两点之间的距离为x，A，D两点之间的距离为y，表示y与x的函数关系的图象如图2所示．则线段AC的长为　   　，线段AB的长为　   　．

三、解答题（共68分）解答应写出文字说明、演算步骤或证明过程。

17．（5分）解方程：x2﹣4x+3＝0．

18．（5分）解方程：x2﹣3x＝0．

19．（5分）关于x的一元二次方程x2+（2m﹣1）x+m2+m﹣2＝0有两个不相等的实数根．

（1）求m的取值范围；

（2）若m为正整数，写出一个符合条件的m的值并求出此时方程的根．

20．（5分）如图1是博物馆展出的古代车轮实物，《周礼•考工记》记载：“…故兵车之轮六尺有六寸，田车之轮六尺有三寸…”据此，我们可以通过计算车轮的半径来验证车轮类型，请将以下推理过程补充完整．

如图2所示，在车轮上取A、B两点，设所在圆的圆心为O，半径为rcm．

作弦AB的垂线OC，D为垂足，则D是AB的中点．其推理依据是：　   　．

经测量：AB＝90cm，CD＝15cm，则AD＝　   　cm；

用含r的代数式表示OD，OD＝　   　cm．

在Rt△OAD中，由勾股定理可列出关于r的方程：

r2＝　   　，

解得r＝75．

通过单位换算，得到车轮直径约为六尺六寸，可验证此车轮为兵车之轮．

21．（6分）已知：如图，线段AB．

求作：以AB为斜边的直角△ABC，使得一个内角等于30°．

作法：①作线段AB的垂直平分线交AB于点O；

②以点O为圆心，OA长为半径画圆；

③以点B为圆心，OB长为半径画弧，与⊙O相交，记其中一个交点为C；

④分别连接AC，BC．

△ABC就是所求作的直角三角形．

（1）使用直尺和圆规，依作法补全图形（保留作图痕迹）；

（2）完成下面的证明．

证明：连接OC，

∵AB是⊙O的直径，

∴∠ACB＝　   　°（　   　）（填推理的依据）．

∴△ABC是以AB为斜边的直角三角形．

∵OC＝OB＝BC，

∴△OBC是等边三角形．

∴∠COB＝60°．

∴∠A＝　   　°．

22．（6分）已知二次函数y＝x2﹣4x+3．

（1）求二次函数y＝x2﹣4x+3图象的顶点坐标；

（2）在平面直角坐标系xOy中，画出二次函数y＝x2﹣4x+3的图象；

（3）当1＜x＜4时，结合函数图象，直接写出y的取值范围．

23．（6分）已知抛物线y＝ax2+2ax+3a2﹣4（a≠0）．

（1）该抛物线的对称轴为　   　；

（2）若该抛物线的顶点在x轴上，求抛物线的解析式；

（3）设点M（m，y1），N（2，y2）在该抛物线上，若y1＞y2，求m的取值范围．

24．（6分）如图，Rt△ABC中，∠ACB＝90°，点D在BC边上，以CD为直径的⊙O与直线AB相切于点E，且E是AB中点，连接OA．

（1）求证：OA＝OB；

（2）连接AD，若AD＝，求⊙O的半径．

25．（6分）如图，AB为⊙O的直径，C为⊙O上一点，D是的中点，过点D作AC的垂线，交AC的延长线于点E，连接AD．

（1）求证：DE是⊙O的切线；

（2）连接CD，若∠CDA＝30°，AC＝2，求CE的长．

26．（6分）在平面直角坐标系xOy中，抛物线y＝ax2+bx（a≠0）过点（4，0）．

（1）用含a的代数式表示b；

（2）已知点A（0，a），将点A绕原点O顺时针旋转90°得到点B，再将点B向右平移2个单位长度得到点C，求点C的坐标（用含a的代数式表示）；

（3）在（2）的条件下，若线段AC与抛物线有公共点，求a的取值范围．

27．（6分）在等腰直角△ABC中，AB＝AC，∠A＝90°，过点B作BC的垂线l．点P为直线AB上的一个动点（不与点A，B重合），将射线PC绕点P顺时针旋转90°交直线l于点D．

（1）如图1，点P在线段AB上，依题意补全图形．

①求证：∠BDP＝∠PCB；

②用等式表示线段BC，BD，BP之间的数量关系，并证明．

（2）点P在线段AB的延长线上，直接写出线段BC，BD，BP之间的数量关系．

28．（6分）在平面直角坐标系xOy中，⊙O的半径为2，A，B为⊙O外两点，AB＝1．给出如下定义：平移线段AB，使线段AB的一个端点落在⊙O上，其他部分不在⊙O外，点A，B的对应点分别为点A'，B'，线段AA'长度的最大值称为线段AB到⊙O的“极大距离”，记为d（AB，⊙O）．

（1）若点A（﹣4，0）．

①当点B为（﹣3，0），如图所示，平移线段AB，在点P1（﹣2，0），P2（﹣1，0），P3（1，0），P4（2，0）中，连接点A与点　   　的线段的长度就是d（AB，⊙O）；

②当点B为（﹣4，1），求线段AB到⊙O的“极大距离”所对应的点A'的坐标．

（2）若点A（﹣4，4），d（AB，⊙O）的取值范围是　   　．

参考答案

一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个。

1．【分析】根据中心对称图形的概念对各选项分析判断即可得解．

【解答】解：A、是中心对称图形，故本选项符合题意；

B、不是中心对称图形，故本选项不合题意；

C、不是中心对称图形，故本选项不合题意；

D、不是中心对称图形，故本选项不合题意．

故选：A．

【点评】本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后与原图重合．

2．【分析】抛物线y＝（x+1）2﹣2开口向上，有最小值，顶点坐标为（﹣1，﹣2），顶点的纵坐标﹣2即为函数的最小值．

【解答】解：根据二次函数的性质，当x＝﹣1时，二次函数y＝（x﹣1）2﹣2的最小值是﹣2．

故选：D．

【点评】本题考查对二次函数最值．求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．

3．【分析】根据关于x的方程ax2﹣2ax+1＝0的一个根是﹣1，可以得到a+2a+1＝0，然后即可得到a的值．

【解答】解：∵关于x的方程ax2﹣2ax+1＝0的一个根是﹣1，

∴a+2a+1＝0，

∴3a+1＝0，

解得a＝﹣，

故选：C．

【点评】本题考查一元二次方程的解，解答本题的关键是明确题意，求出a的值．

4．【分析】根据方程的系数结合根的判别式Δ＝b2﹣4ac，可分别找出四个选项中方程的根的判别式△的值，取Δ＜0的选项即可得出结论．

【解答】解：A、∵Δ＝32﹣4×1×0＝9＞0，

∴方程x2+3x＝0有两个不相等的实数根，选项A不符合题意；

B、∵Δ＝22﹣4×1×（﹣1）＝8＞0，

∴方程x2+2x﹣1＝0有两个不相等的实数根，选项B不符合题意；

C、∵Δ＝22﹣4×1×1＝0，

∴方程x2+2x+1＝0有两个相等的实数根，选项C不符合题意；

D、∵Δ＝（﹣1）2﹣4×1×3＝﹣11＜0，

∴方程x2﹣x+3＝0没有实数根，选项D符合题意．

故选：D．

【点评】本题考查了根的判别式，牢记“当Δ＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程无实数根”是解题的关键．

5．【分析】连接OA，先由垂径定理求出AC的长，再由勾股定理求出OC的长，进而可得出结论．

【解答】解：连接OA，如图所示：

∵⊙O的直径为10分米，

∴OA＝5分米，

由题意得：OD⊥AB，AB＝8分米，

∴AC＝BC＝AB＝4分米，

∴OC＝＝＝3（分米），

∴水的最大深度CD＝OD﹣OC＝5﹣3＝2（分米），

故选：A．

【点评】本题考查的是垂径定理的应用以及勾股定理，根据勾股定理求出OC的长是解答此题的关键．

6．【分析】利用切线长定理、等腰三角形的性质即可得出答案．

【解答】解：由切线长定理可得：∠APO＝∠BPO，PA＝PB，从而AB⊥OP，AD＝BD．

因此A．B．C都正确．

无法得出∠PAB＝∠APB，可知：D是错误的．

综上可知：只有D是错误的．

故选：D．

【点评】本题考查了切线长定理、等腰三角形的性质，关键是利用切线长定理、等腰三角形的性质解答．

7．【分析】根据表格中的数据和二次函数的性质，可以判断各个选项中的结论是否正确，本题得以解决．

【解答】解：由表格可知，

该函数的对称轴是直线x＝＝﹣，故选项B错误，

该抛物线开口向上，在x＝﹣时，取得最小值，故选项A错误，

当x＞﹣时，y随x的增大而最大，故选项D错误，

当x＝0时，y＝4，则抛物线G与y轴的交点坐标为（0，4），故选项C正确；

故选：C．

【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征、二次函数的最值，解答本题的关键是明确题意，利用二次函数的性质解答．

8．【分析】根据直线y＝kx与抛物线y2＝ax2+bx+c相交于M、N两点，可以得到方程kx＝ax2+bx+c有两个不同的根，从而可以得到函数y＝ax2+（b﹣k）x+c与x轴的交点个数和交点的正负情况，本题得以解决．

【解答】解：∵抛物线y＝ax2+bx+c与直线y＝kx交于M，N两点，

∴kx＝ax2+bx+c有两个不同的根，

即ax2+（b﹣k）x+c＝0有两个不同的根且都小于0，

∴函数y＝ax2+（b﹣k）x+c与x轴两个交点且都在x轴的负半轴，

故选：A．

【点评】本题考查二次函数的性质、一元二次方程与二次函数的关系、抛物线与x轴的交点，解答本题的关键是明确题意，利用数形结合的思想解答．

二、填空题（共16分，每题2分）

9．【分析】关于原点对称的点，横坐标与纵坐标都互为相反数．

【解答】解：根据关于原点对称的点，横坐标与纵坐标都互为相反数，

可知点A（1，3）关于原点的对称点坐标是（﹣1，﹣3）．

【点评】解决本题的关键是掌握好对称点的坐标规律：

（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；

（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；

（3）关于原点对称的点，横坐标与纵坐标都互为相反数．

10．【分析】根据图象的平移规律，可得答案．

【解答】解：将抛物线y＝x2沿着y轴正方向平移2个单位长度，所得抛物线的解析式为y＝x2+2；将抛物线y＝x2沿着y轴负方向平移2个单位长度，所得抛物线的解析式为y＝x2﹣2；

故答案是：y＝x2+2或y＝x2﹣2．

【点评】本题主要考查了二次函数与几何变换问题，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．

11．【分析】利用判别式得到Δ＝（﹣2）2﹣4×（﹣m）＞0，然后解不等式即可．

【解答】解：根据题意得Δ＝（﹣2）2﹣4×（﹣m）＞0，

解得m＞﹣1．

故答案为：m＞﹣1．

【点评】本题考查了二次函数与x轴的交点，把求二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解一元二次方程ax2+bx+c＝0．△＝b2﹣4ac决定抛物线与x轴的交点个数．

12．【分析】设月平均增长率为x，根据6月及8月的盈利，即可得出关于x的一元二次方程，此题得解．

【解答】解：设月平均增长率为x，

根据题意得：24000（1+x）2＝34560．

故答案为：24000（1+x）2＝34560．

【点评】本题考查了一元二次方程中增长率的知识．增长前的量×（1+年平均增长率）年数＝增长后的量．

13．【分析】根据勾股定理的逆定理解答即可．

【解答】解：∵AP2＝32+32＝18，AC2＝36，PC2＝32+32＝18，

∴AC2＝AP2+PC2，

∴∠APC＝90°，

∴∠BPC＝∠APC﹣∠APB＝90°﹣α，

故答案为：90°﹣α．

【点评】此题考查勾股定理的逆定理，关键是根据勾股定理的逆定理得出∠APC＝90°解答．

14．【分析】连接OB、OC，根据正方形的性质，易得出∠BOC＝90°，根据圆周角定理，可求出∠BEC＝45°．

【解答】解：连接OB、OC，则∠E＝∠BOC，

∵O是正方形外接圆的圆心，

∴∠BOC＝90°，

∴∠BEC＝∠BOC＝45°．

【点评】正确理解圆心角与圆周角的关系是解决本题的关键．

15．【分析】连接OA，过O点作OE⊥AB，OF⊥AC，如图，根据等腰三角形的性质得到AO平分∠BAC，则利用角平分线的性质得OE＝OF，接着根据切线的性质可判断OE为⊙O的半径，然后根据切线的判定定理可判断AC与⊙O相切．

【解答】解：连接OA，过O点作OE⊥AB，OF⊥AC，如图，

∵O是等腰△ABC的底边BC的中点，

∴AO平分∠BAC，

∵OE⊥AB，OF⊥AC，

∴OE＝OF，

∵腰AB与⊙O相切，

∴OE为⊙O的半径，

∴OF为⊙O的半径，

而OF⊥AC，

∴AC与⊙O相切．

故答案为相切．

【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了等腰三角形的性质、角平分线的性质和切线的判定．

16．【分析】从图象看，当x＝1时，y＝，即BD＝1时，AD＝，当x＝7时，y＝，即BD＝7时，C、D重合，此时y＝AD＝AC＝，则CD＝6，即当BD＝1时，△ADC为以点A为顶点腰长为的等腰三角形，进而求解．

【解答】解：从图象看，当x＝1时，y＝，即BD＝1时，AD＝，

当x＝7时，y＝，即BD＝7时，C、D重合，此时y＝AD＝AC＝，则CD＝6，

即当BD＝1时，△ADC为以点A为顶点腰长为的等腰三角形，如下图：

过点A作AH⊥BC于点H，

在Rt△ACH中，AC＝，CH＝DH＝CD＝3，则AH＝＝＝2，

在Rt△ABH中，AB＝＝＝2，

故答案为：，2．

【点评】本题考查的是动点问题的函数图象，此类问题关键是：弄清楚不同时间段，图象和图形的对应关系，进而求解．

三、解答题（共68分）解答应写出文字说明、演算步骤或证明过程。

17．【分析】利用因式分解法解出方程．

【解答】解：x2﹣4x+3＝0

（x﹣1）（x﹣3）＝0

x﹣1＝0，x﹣3＝0

x1＝1，x2＝3．

【点评】本题考查的是一元二次方程的解法，掌握因式分解法解一元二次方程的一般步骤是解题的关键．

18．【分析】将方程左边的多项式提取公因式x，分解因式后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程，求出一次方程的解即可得到原方程的解．

【解答】解：x2﹣3x＝0，

分解因式得：x（x﹣3）＝0，

可得：x＝0或x﹣3＝0，

解得：x1＝0，x2＝3．

【点评】此题考查了解一元二次方程﹣因式分解法，利用因式分解法解方程时，首先将方程右边化为0，左边化为积的形式，然后利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．

19．【分析】（1）根据方程的系数结合根的判别式Δ＞0，即可得出关于m的一元一次不等式，解之即可得出m的取值范围；

（2）由（1）的结论结合m为正整数可得出m的值，将其代入原方程后解之即可得出结论．

【解答】解：（1）∵关于x的一元二次方程x2+（2m﹣1）x+m2+m﹣2＝0有两个不相等的实数根，

∴Δ＝（2m﹣1）2﹣4×1×（m2+m﹣2）＞0，

∴﹣8m+9＞0，

∴m＜．

（2）∵m为正整数，且m＜，

∴m＝1，

∴原方程为x2+x＝0，

∴x（x+1）＝0，

∴x1＝0，x2＝﹣1．

【点评】本题考查了根的判别式以及因式分解法解一元二次方程，解题的关键是：（1）牢记“当Δ＞0时，方程有两个不相等的实数根”；（2）利用因式分解法解出一元二次方程．

20．【分析】根据垂径定理，利用勾股定理构建方程求解即可．

【解答】解：如图2所示，在车轮上取A、B两点，设所在圆的圆心为O，半径为rcm．

作弦AB的垂线OC，D为垂足，则D是AB的中点．其推理依据是：垂直弦的直径平分弦．

经测量：AB＝90cm，CD＝15cm，则AD＝45cm；

用含r的代数式表示OD，OD＝（r﹣15）cm．

在Rt△OAD中，由勾股定理可列出关于r的方程：

r2＝452+（r﹣15）2，

解得r＝75．

通过单位换算，得到车轮直径约为六尺六寸，可验证此车轮为兵车之轮．

故答案为：垂直弦的直径平分弦，45，（r﹣15），452+（r﹣15）2．

【点评】本题考查垂径定理，勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．

21．【分析】（1）根据要求作出图形即可．

（2）证明△BOC是等边三角形，∠ACB＝90°即可解决问题．

【解答】解：（1）如图，△ABC即为所求作．

（2）连接OC，

∵AB是⊙O的直径，

∴∠ACB＝90°（直径所对的圆周角是直角）（填推理的依据）．

∴△ABC是以AB为斜边的直角三角形．

∵OC＝OB＝BC，

∴△OBC是等边三角形．

∴∠COB＝60°．

∴∠A＝30°．

故答案为：90，直径所对的圆周角是直角，30．

【点评】本题考查作图﹣复杂作图，圆周角定理，等边三角形的判定和性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．

22．【分析】（1）把一般式配成顶点式得到抛物线的顶点坐标；

（2）先确定抛物线与坐标轴的交点坐标，然后利用描点法画出二次函数图象；

（3）结合二次函数图象，写出当1＜x＜4时对应的y的取值范围．

【解答】解：（1）∵y＝x2﹣4x+3＝（x﹣2）2﹣1，

∴该二次函数图象顶点坐标为（2，﹣1）；

（2）当y＝0时，x2﹣4x+3＝0，解得x1＝1，x2＝3，

∴抛物线与x轴的交点坐标为（1，0），（3，0）；

当x＝0时，y＝x2﹣4x+3＝3，则抛物线与y轴的交点坐标为（0，3），

如图：

；

（3）由图象可知，当1＜x＜4时，﹣1≤y＜3．

【点评】本题考查了二次函数的图象和性质，二次函数图形上点的坐标特征，数形结合是解题的关键．

23．【分析】（1）根据题意可得抛物线的对称轴；

（2）抛物线的顶点在x轴上，可得顶点坐标为（﹣1，0），进而可得a的值；

（3）根据点N（2，y2）关于直线x＝﹣1的对称点为N′（﹣4，y2），进而可得m的取值范围．

【解答】解：（1）∵抛物线y＝ax2+2ax+3a2﹣4．

∴对称轴为直线x＝＝﹣1，

故答案为：直线x＝﹣1；

（2）y＝ax2+2ax+3a2﹣4

＝a（x+1）2+3a2﹣a﹣4，

∵抛物线顶点在x轴上，

即当x＝﹣1时，y＝0，

∴3a2﹣a﹣4＝0，

解得．

∴抛物线解析式为y＝﹣x2﹣2x﹣1或．

（3）∵抛物线的对称轴为直线x＝﹣1，

∴N（2，y2）关于直线x＝﹣1的对称点为N’（﹣4，y2）．

（ⅰ）当a＞0时，若y1＞y2，则m＜﹣4或m＞2；

（ⅱ）当a＜0时，若y1＞y2，则﹣4＜m＜2．

【点评】本题考查的待定系数法求二次函数的解析式，二次函数的性质，二次函数图象上点的坐标特征，要求学生非常熟悉函数与坐标轴的交点、顶点等点，代表的意义及函数特征等．

24．【分析】（1）连接OE，如图，根据切线的性质得OE⊥AB，则可判断OE垂直平分AB，根据线段垂直平分线的性质得到结论；

（2）设⊙O的半径为r，先证明AO平分∠BAC，再证明∠OAC＝∠B＝∠OAB＝30°，所以AC＝OC＝r，利用勾股定理得到（r）2+（2r）2＝（）2，然后解方程即可．

【解答】（1）证明：连接OE，如图，

∵以CD为直径的⊙O与直线AB相切于点E，

∴OE⊥AB，

∵E是AB中点，

∴OE垂直平分AB，

∴OA＝OB；

（2）解：设⊙O的半径为r，

∵OE⊥AB，OC⊥AC，OE＝OC，

∴AO平分∠BAC，

∴∠OAC＝∠OAB，

∵OA＝OB，

∴∠B＝∠OAB，

∴∠OAC＝∠B＝∠OAB＝30°，

在Rt△OAC中，AC＝OC＝r，

在Rt△ACD中，（r）2+（2r）2＝（）2，解得r＝1，

即⊙O的半径为1．

【点评】本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了角平分线的性质．

25．【分析】（1）连接OD，根据圆周角定理得到∠BAD＝∠CAD，根据等腰三角形的性质得到∠BAD＝∠ODA，求得∠CAD＝∠ODA，得到OD∥AE，根据平行线的性质得到DE⊥OD，根据切线的判定定理得到DE是⊙O的切线；

（2）连接OC，CD，根据圆周角定理得到∠AOC＝2∠CDA＝60°，求得△AOC是等边三角形，推出四边形ACDO是菱形，得到CD＝AC＝2，∠CDE＝30°，根据直角三角形的性质得到CE＝1．

【解答】（1）证明：连接OD，

∵D是的中点，

∴∠BAD＝∠CAD，

∵OA＝OD，

∴∠BAD＝∠ODA，

∴∠CAD＝∠ODA，

∴OD∥AE，

∵DE⊥AC，

∴DE⊥OD，

∴DE是⊙O的切线；

（2）解：连接OC，CD，

∵∠CDA＝30°，

∴∠AOC＝2∠CDA＝60°，

∴△AOC是等边三角形，

∴由（1）可得，四边形ACDO是菱形，

∴CD＝AC＝2，∠CDE＝30°，

∴CE＝1．

【点评】本题主要考查了切线的判定，圆周角定理，平行线的性质及判定定理，解题的关键是学会添加常用辅助线，属于中考常考题型．

26．【分析】（1）将（4，0）代入即可得答案，

（2）y轴上的点绕原点O顺时针旋转90°到x轴，向右平移则横坐标加2即可求出B的坐标，

（3）根据图形列出不等式可得a的范围；

【解答】解：（1）∵抛物线y＝ax2+bx过点（4，0），

∴0＝16a+4b，

∴b＝﹣4a．

（2）∵点A（0，a）绕原点O顺时针旋转90°得到点B，

∴点B的坐标为（a，0），

∵点B向右平移2个单位长度得到点C，

∴点C的坐标为（a+2，0）．

（3）（i）当a＞0时，

抛物线y＝ax2﹣4ax开口向上，与x轴交于两点（0，0），（4，0）．

若线段AC与抛物线有公共点（如答图1），只需满足：，解得：a≥2；

（ii）当a＜0时，

抛物线y＝ax2﹣4ax开口向下，与x轴交于两点（0，0），（4，0），

若线段AC与抛物线有公共点（如答图2），只需满足：，解得：a≤﹣2；

综上所述，a的取值范围为a≥2或a≤﹣2．

【点评】本题考查二次函数解析式，点的旋转、平移与坐标以及线段与抛物线的交点，数形结合，画出图形便可以分析得到答案．

27．【分析】（1）①根据题意补全图形，由直角三角形的性质可得出答案；

②过点P作PF⊥BP交BC于点F，证明△BPD≌△FPC（AAS），由全等三角形的性质得出BD＝FC，由等腰直角三角形的性质可得出结论；

（2）过点P作PM⊥PB交BD于点M，证明△PMD≌△PBC（AAS），由全等三角形的性质可得出DM＝BC，则可得出结论．

【解答】解：（1）①补全图形如图1，

证明：如图1，设PD与BC的交点为点E，

根据题意可知，∠CPD＝90°，

∵BC⊥l，

∴∠DBC＝90°，

∴∠BDP+∠BED＝∠PCB+∠PEC＝90°，

∴∠BDP＝∠PCB；

②BC﹣BD＝BP．

证明：如图2，过点P作PF⊥BP交BC于点F，

∵AB＝AC，∠A＝90°，

∴∠ABC＝45°，

∴BP＝BF，∠PFB＝45°，

∴∠PBD＝∠PFC＝135°，

又∵∠BDP＝∠PCF，

∴△BPD≌△FPC（AAS），

∴BD＝FC，

在等腰直角△BPF中，BF＝BP，

∴BC﹣BD＝BP．

（2）BD﹣BC＝BP．

证明：如图3，过点P作PM⊥PB交BD于点M，

由（1）可知∠ABC＝∠PBM＝45°，

∴∠PBM＝∠PMB＝45°，

∴PB＝PM，∠PBC＝∠PCB＝135°，

同（1）可得∠PDB＝∠PCB，

∴△PMD≌△PBC（AAS），

∴DM＝BC，

∵PB＝PM，∠BPM＝90°，

∴BM＝PB，

∴BD﹣DM＝BM＝BD﹣BC＝PB．

【点评】此题是三角形综合题，主要考查了旋转的性质，等腰直角三角形的判定和性质，全等三角形的判定和性质，熟练掌握等腰直角三角形的性质及全等三角形的判定与性质是解本题的关键．

28．【分析】（1）①根据线段AB到⊙O的“极大距离”的定义判断即可．

②如图1中，设A′B′交x轴于M，连接OA′．解直角三角形求出OM，可得结论．

（2）如图2中，由题意，点B的运动轨迹是以A为圆心，1为半径的⊙A．求出d（AB，⊙O）的最大值与最小值可得结论．

【解答】解：（1）①根据线段AB到⊙O的“极大距离”的定义可知：

连接点A与点P3的线段的长度就是d（AB，⊙O），

故答案为：P3．

②如图1中，设A′B′交x轴于M，连接OA′．

∵OM⊥A′B′，

∴A′M＝B′M＝，

∴OM＝＝＝，

∴A′（，﹣）．

（2）如图2中，由题意，点B的运动轨迹是以A为圆心，1为半径的⊙A．

当线段BA平移到B′A′时，d（AB，⊙O）的值最大，最大值＝4+2，

当线段AB平移到A′B′时，d（AB，⊙O）的值最小，最小值＝4+1，

∴4+1≤d（AB，⊙O）≤4+2．

故答案为：4+1≤d（AB，⊙O）≤4+2．

【点评】本题属于圆综合题，考查了线段AB到⊙O的“极大距离”的定义，解直角三角形等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．