
2023年中考数学精选真题实战测试50 锐角三角函数 B
展开
这是一份2023年中考数学精选真题实战测试50 锐角三角函数 B,共15页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
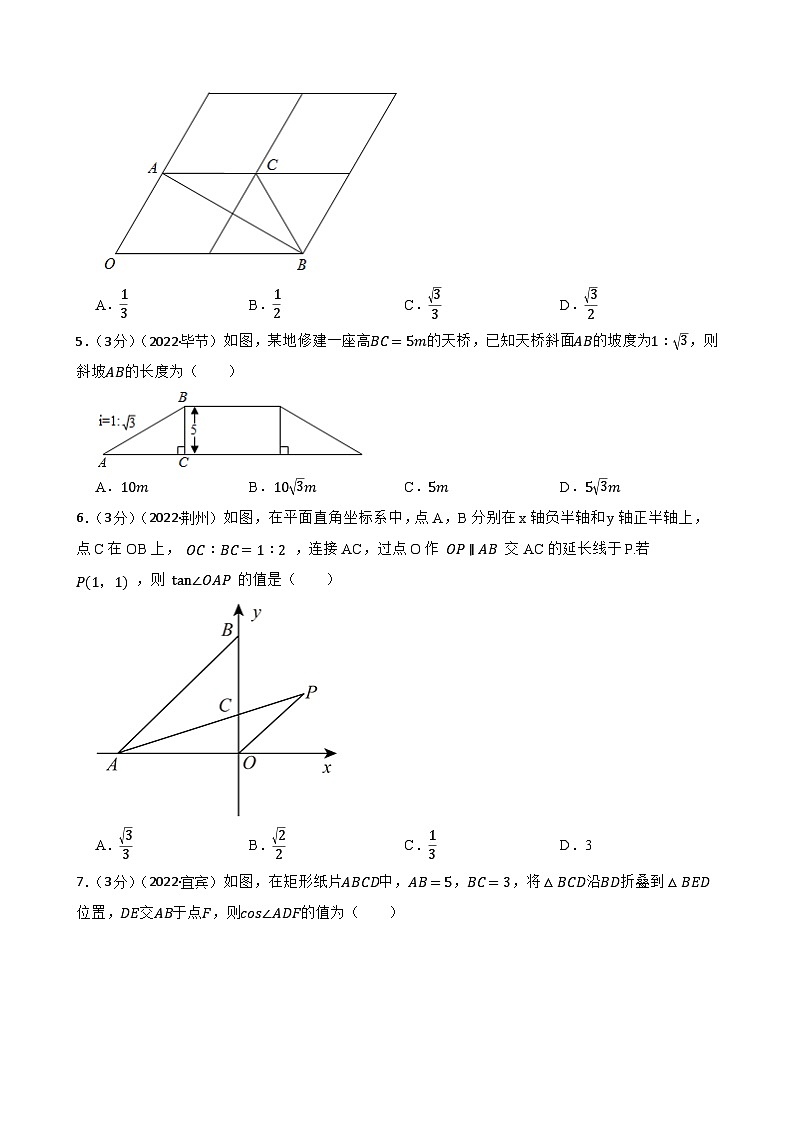
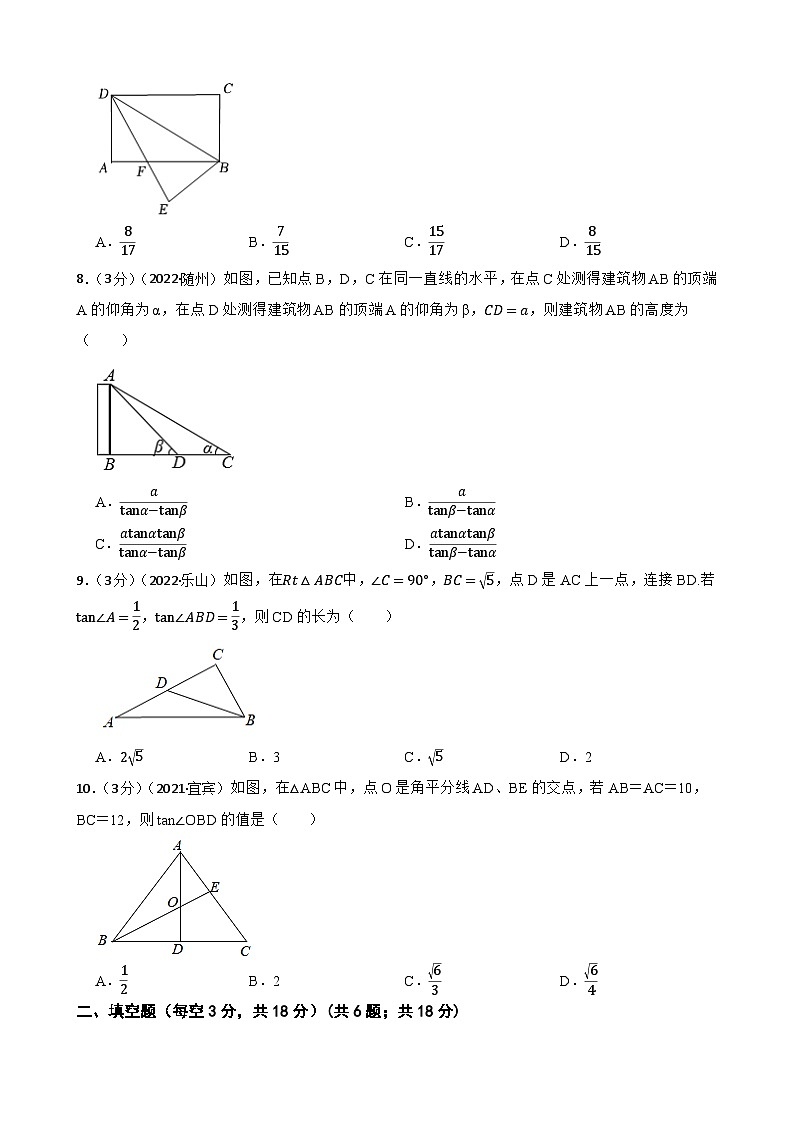
2023年中考数学精选真题实战测试50 锐角三角函数 B一、单选题(每题3分,共30分)(共10题;共30分)1.(3分)(2022·天津)的值等于( )A.2 B.1 C. D.2.(3分)(2022·济南)数学活动小组到某广场测量标志性建筑AB的高度.如图,他们在地面上C点测得最高点A的仰角为22°,再向前70m至D点,又测得最高点A的仰角为58°,点C,D,B在同一直线上,则该建筑物AB的高度约为( )(精确到1m.参考数据:,,,)A.28m B.34m C.37m D.46m3.(3分)(2022·贵港)如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为,在点B处测得树顶C的仰角为,且A,B,D三点在同一直线上,若,则这棵树的高度是( )A. B. C. D.4.(3分)(2022·仙桃)由4个形状相同,大小相等的菱形组成如图所示的网格,菱形的顶点称为格点,点A,B,C都在格点上,∠O=60°,则tan∠ABC=( )A. B. C. D.5.(3分)(2022·毕节)如图,某地修建一座高的天桥,已知天桥斜面的坡度为,则斜坡的长度为( )A. B. C. D.6.(3分)(2022·荆州)如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上, ,连接AC,过点O作 交AC的延长线于P.若 ,则 的值是( ) A. B. C. D.37.(3分)(2022·宜宾)如图,在矩形纸片中,,,将沿折叠到位置,交于点,则的值为( )A. B. C. D.8.(3分)(2022·随州)如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β,,则建筑物AB的高度为( ) A. B.C. D.9.(3分)(2022·乐山)如图,在中,,,点D是AC上一点,连接BD.若,,则CD的长为( )A. B.3 C. D.210.(3分)(2021·宜宾)如图,在△ABC中,点O是角平分线AD、BE的交点,若AB=AC=10,BC=12,则tan∠OBD的值是( )A. B.2 C. D.二、填空题(每空3分,共18分)(共6题;共18分)11.(3分)(2022·益阳)如图,在Rt△ABC中,∠C=90°,若sinA=,则cosB= . 12.(3分)(2022·宁夏)2022年4月16日9时56分,神舟十三号载人飞船返回舱在东风着陆场成功着陆,某一时刻观测点D测得返回舱底部C的仰角∠CDE=45°,降落伞底面圆A点处的仰角∠ADE=46°12′.已知半径OA长14米,拉绳AB长50米,返回舱高度BC为2米,这时返回舱底部离地面的高度CE约为 米(精确到米).(参考数据:,,)13.(3分)(2022·湘西)阅读材料:余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理,运用它可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题.余弦定理是这样描述的:在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍.用公式可描述为:a2=b2+c2﹣2bccosAb2=a2+c2﹣2accosBc2=a2+b2﹣2abcosC现已知在△ABC中,AB=3,AC=4,∠A=60°,则BC= .14.(3分)(2022·常州)如图,在四边形中,,平分.若,,则 .15.(3分)(2022·绥化)定义一种运算;,.例如:当,时,,则的值为 .16.(3分)(2022·孝感)如图,有甲乙两座建筑物,从甲建筑物点处测得乙建筑物点的俯角为,点的俯角为,为两座建筑物的水平距离.已知乙建筑物的高度为,则甲建筑物的高度为 .(,,,结果保留整数). 三、解答题(共10题,共72分)(共10题;共72分)17.(5分)(2022·贺州)计算: .18.(5分)(2022·娄底)计算:.19.(5分)(2022·广元)计算:2sin60°﹣|﹣2|+(π﹣)0﹣+(﹣)﹣2.20.(6分)(2022·镇江)如图1是一张圆凳的造型,已知这张圆凳的上、下底面圆的直径都是,高为.它被平行于上、下底面的平面所截得的横截面都是圆.小明画出了它的主视图,是由上、下底面圆的直径、以及、组成的轴对称图形,直线为对称轴,点、分别是、的中点,如图2,他又画出了所在的扇形并度量出扇形的圆心角,发现并证明了点在上.请你继续完成长的计算. 参考数据:,,,,,.21.(8分)(2022·日照)2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情.如图是某滑雪场的横截面示意图,雪道分为AB,BC两部分,小明同学在C点测得雪道BC的坡度i=1:2.4,在A点测得B点的俯角∠DAB=30°.若雪道AB长为270m,雪道BC长为260m.(1)(4分)求该滑雪场的高度h;(2)(4分)据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3,且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.22.(8分)(2022·贵阳)交通安全心系千万家.高速公路管理局在某隧道内安装了测速仪,如图所示的是该段隧道的截面示意图.测速仪和测速仪到路面之间的距离,测速仪和之间的距离,一辆小汽车在水平的公路上由西向东匀速行驶,在测速仪处测得小汽车在隧道入口点的俯角为25°,在测速仪处测得小汽车在点的俯角为60°,小汽车在隧道中从点行驶到点所用的时间为38s(图中所有点都在同一平面内).
(1)(4分)求,两点之间的距离(结果精确到1m);(2)(4分)若该隧道限速22m/s,判断小汽车从点行驶到点是否超速?通过计算说明理由.(参考数据:,,,,,)23.(8分)(2022·内江)如图所示,九(1)班数学兴趣小组为了测量河对岸的古树A、B之间的距离,他们在河边与AB平行的直线l上取相距60m的C、D两点,测得∠ACB=15°,∠BCD=120°,∠ADC=30°.(1)(4分)求河的宽度;(2)(4分)求古树A、B之间的距离.(结果保留根号)24.(8分)(2022·重庆)如图,三角形花园ABC紧邻湖泊,四边形ABDE是沿湖泊修建的人行步道.经测量,点C在点A的正东方向,AC=200米.点E在点A的正北方向.点B,D在点C的正北方向,BD=100米.点B在点A的北偏东30°,点D在点E的北偏东45°.(1)(4分)求步道DE的长度(精确到个位);(2)(4分)点D处有直饮水,小红从A出发沿人行步道去取水,可以经过点B到达点D,也可以经过点E到达点D.请计算说明他走哪一条路较近?(参考数据: 25.(9分)(2022·攀枝花)第24届冬奥会(也称2022年北京冬奥会)于2022年2月4日至2月20日在中国北京举行,北京成为了历史上第一座既举办过夏奥会又举办过冬奥会的城市.冬奥会上跳台滑雪是一项极为壮观的运动.运动员经过助滑、起跳、空中飞行和着陆,整个动作连贯一致,一气呵成,如图,某运动员穿着滑雪板,经过助滑后,从倾斜角的跳台A点以速度沿水平方向跳出,若忽略空气阻力影响,水平方向速度将保持不变.同时,由于受重力作用,运动员沿竖直方向会加速下落,因此,运动员在空中飞行的路线是抛物线的一部分,已知该运动员在B点着陆,,且.忽略空气阻力,请回答下列问题:(1)(3分)求该运动员从跳出到着陆垂直下降了多少m?(2)(3分)以A为坐标原点建立直角坐标系,求该抛物线表达式;(3)(3分)若该运动员在空中共飞行了4s,求他飞行2s后,垂直下降了多少m?26.(10分)(2022·海南)无人机在实际生活中应用广泛.如图8所示,小明利用无人机测量大楼的高度,无人机在空中P处,测得楼楼顶D处的俯角为,测得楼楼顶A处的俯角为.已知楼和楼之间的距离为100米,楼的高度为10米,从楼的A处测得楼的D处的仰角为(点A,B,C,D、P在同一平面内).(1)(2分)填空: 度, 度;(2)(3分)求楼的高度(结果保留根号);(3)(3分)求此时无人机距离地面的高度.
答案解析部分1.【答案】B2.【答案】C3.【答案】A4.【答案】C5.【答案】A6.【答案】C7.【答案】C8.【答案】D9.【答案】C10.【答案】A11.【答案】12.【答案】161413.【答案】14.【答案】15.【答案】16.【答案】1617.【答案】解:原式 18.【答案】解:.19.【答案】解:2sin60°﹣|﹣2|+(π﹣)0﹣+(﹣)﹣2=2×-2++1-2+4=-2++1-2+4=3.20.【答案】解:连接 ,交 于点 .设直线 交 于点 . ∵ 是 的中点,点 在 上,∴ .在 中,∵ , ,∴ , .∵直线 是对称轴,∴ , , ,∴ .∴ .∴ , .在 中, ,即 ,则 .∵ ,即 ,则 .∴ .∵该图形为轴对称图形,张圆凳的上、下底面圆的直径都是 , ,∴ .∴ .21.【答案】(1)解:过B作BF∥AD,过A过AF⊥AD,两直线交于F,过B作BE垂直地面交地面于E,如图:根据题知∠ABF=∠DAB=30°,∴,∵BC的坡度i=1:2.4,∴BE:CE=1:2.4,设BE=tm,则CE=2.4tm,∵BE2+CE2=BC2,∴t2+(2.4t)2=2602,解得t=100(m),(负值已舍去),∴h=AF+BE=235(m),答:该滑雪场的高度h为235m;(2)解:设甲种设备每小时的造雪量是xm3,则乙种设备每小时的造雪量是(x+35)m3,根据题意得:,解得x=15,经检验,x=15是原方程的解,也符合题意,∴x+35=50,答:甲种设备每小时的造雪量是15m3,则乙种设备每小时的造雪量是50m3.22.【答案】(1)解:四边形是平行四边形四边形是矩形,在中,在中,答:,两点之间的距离为760米;(2)解:, 小汽车从点行驶到点未超速.23.【答案】(1)解:过点A作AE⊥l,垂足为E,设CE=x米,∵CD=60米,∴DE=CE+CD=(x+60)米,∵∠ACB=15°,∠BCD=120°,∴∠ACE=180°﹣∠ACB﹣∠BCD=45°,在Rt△AEC中,AE=CE•tan45°=x(米),在Rt△ADE中,∠ADE=30°,∴tan30°===,∴x=30+30,经检验:x=30+30是原方程的根,∴AE=(30+30)米,∴河的宽度为(30+30)米;(2)解:过点B作BF⊥l,垂足为F,则CE=AE=BF=(30+30)米,AB=EF,∵∠BCD=120°,∴∠BCF=180°﹣∠BCD=60°,在Rt△BCF中,CF===(30+10)米,∴AB=EF=CE﹣CF=30+30﹣(30+10)=20(米),∴古树A、B之间的距离为20米.24.【答案】(1)解:如图,过E作BC的垂线,垂足为H,
∴∠CAE=∠C=∠CHE=90°,
∴四边形ACHE是矩形,
∴EH=AC=200米,DE=EH=200≈283米;(2)解:由题意得:∠ABC=∠BAE=30°,
在Rt△ABC中,
AB=2AC=400,
∴经过点B到达点D,总路程为AB+BD=500,
∵BC==200 ,
∴AE=CH=BC+BD-DH=200 +100-200=200 -100,
经过点E到达点D,总路程为200 +200 -100≈529>500,
故经过点B到达点D较近.25.【答案】(1)解:如图,以A为原点,建立平面直角坐标系.过点B作轴于点D.在中,,答:该运动员从跳出到着陆垂直下降了90m;(2)解:在中,,,由题意抛物线顶点为,经过.设抛物线的解析式为,则有,,抛物线的解析式为.(3)解:当时,,他飞行2s后,垂直下降了22.5m.26.【答案】(1)75;60(2)解:由题意得:米,.在中,,∴,∴∴楼的高度为米.(3)解:作于点G,交于点F,则∵,∴.∵,∴.∵,∴.∵,∴.∴.∴.∴(AAS).∴.∴∴无人机距离地面的高度为110米.
相关试卷
这是一份中考数学精选真题实战测试40 菱形 B,共18页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份中考数学精选真题实战测试28 图形的基础知识 B,共12页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份2023年中考数学精选真题实战测试50 锐角三角函数 B,共15页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。









