


专题17 实际应用综合题-备战宁波中考数学真题模拟题分类汇编
展开专题17 实际应用综合题
1.(•宁波)为了落实劳动教育,某学校邀请农科院专家指导学生进行小番茄的种植,经过试验,其平均单株产量千克与每平方米种植的株数,且为整数)构成一种函数关系.每平方米种植2株时,平均单株产量为4千克;以同样的栽培条件,每平方米种植的株数每增加1株,单株产量减少0.5千克.
(1)求关于的函数表达式.
(2)每平方米种植多少株时,能获得最大的产量?最大产量为多少千克?
【答案】(1)关于的函数表达式为,,且为整数);(2)每平方米种植5株时,能获得最大的产量,最大产量为12.5千克
【详解】(1)每平方米种植的株数每增加1株,单株产量减少0.5千克,
,
答:关于的函数表达式为,,且为整数);
(2)设每平方米小番茄产量为千克,
根据题意得:,
,
当时,取最大值,最大值为12.5,
答:每平方米种植5株时,能获得最大的产量,最大产量为12.5千克.
2.(2021•宁波)某通讯公司就手机流量套餐推出三种方案,如下表:
方案
方案
方案
每月基本费用(元
20
56
266
每月免费使用流量(兆
1024
无限
超出后每兆收费(元
,,三种方案每月所需的费用(元与每月使用的流量(兆之间的函数关系如图所示.
(1)请直接写出,的值.
(2)在方案中,当每月使用的流量不少于1024兆时,求每月所需的费用(元与每月使用的流量(兆)之间的函数关系式.
(3)在这三种方案中,当每月使用的流量超过多少兆时,选择方案最划算?
【答案】(1),;(2);(3)当每月使用的流量超过3772兆时,选择方案最划算
【详解】(1)根据题意,,
;
(2)设在方案中,当每月使用的流量不少于1024兆时,每月所需的费用(元与每月使用的流量(兆)之间的函数关系式为,
把,代入,得:
,解得,
关于的函数关系式为;
(3)花费266元方案可用流量:(兆,
花费266元方案可用流量:(兆,
由图象得,当每月使用的流量超过3772兆时,选择方案最划算.
3.(2020•宁波),两地相距200千米.早上货车甲从地出发将一批物资运往地,行驶一段路程后出现故障,即刻停车与地联系.地收到消息后立即派货车乙从地出发去接运甲车上的物资.货车乙遇到甲后,用了18分钟将物资从货车甲搬运到货车乙上,随后开往地.两辆货车离开各自出发地的路程(千米)与时间(小时)的函数关系如图所示.(通话等其他时间忽略不计)
(1)求货车乙在遇到货车甲前,它离开出发地的路程关于的函数表达式.
(2)因实际需要,要求货车乙到达地的时间比货车甲按原来的速度正常到达地的时间最多晚1个小时,问货车乙返回地的速度至少为每小时多少千米?
【答案】(1);(2)货车乙返回地的车速至少为75千米小时
【详解】(1)设函数表达式为,
把,代入,得,
解得:,
关于的函数表达式为;
由图可知(千米),(小时),(小时),
的取值范围是.
货车乙在遇到货车甲前,它离开出发地的路程关于的函数表达式为;
(2)当时,
,
解得,
由图可知,甲的速度为(千米小时),
货车甲正常到达地的时间为(小时),
(小时),(小时),(小时),
设货车乙返回地的车速为千米小时,
,
解得.
答:货车乙返回地的车速至少为75千米小时.
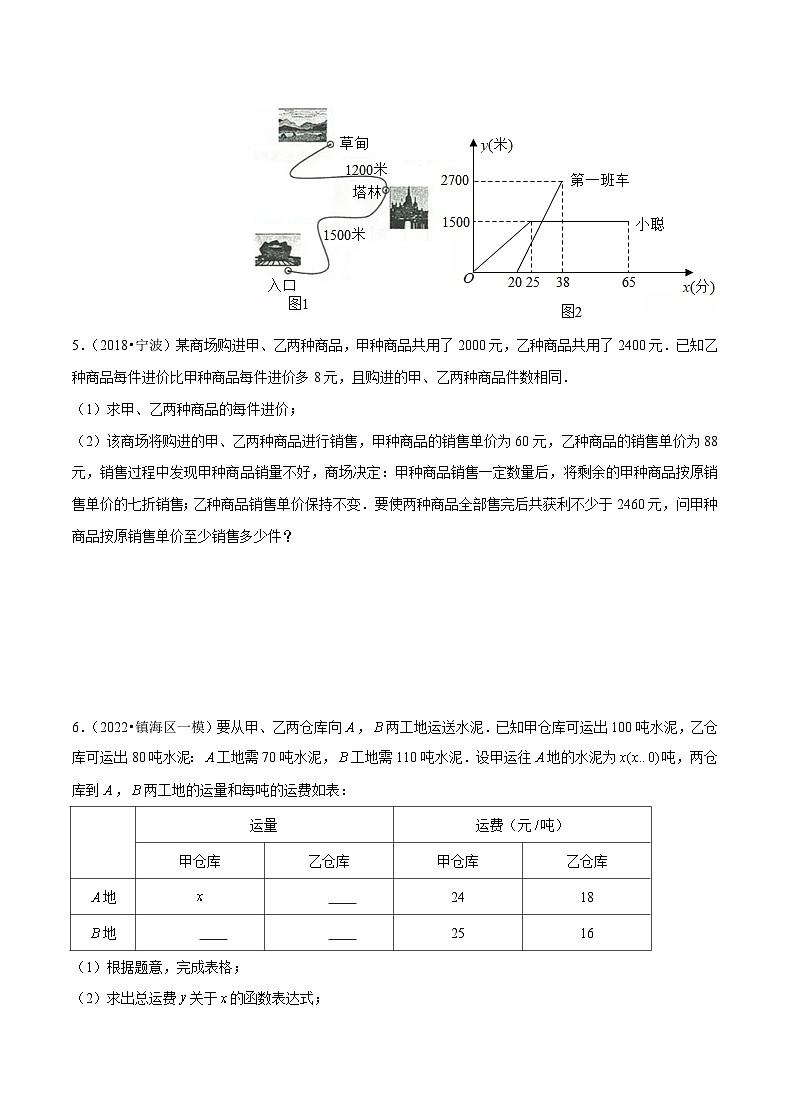
4.(2019•宁波)某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程(米与时间(分的函数关系如图2所示.
(1)求第一班车离入口处的路程(米与时间(分的函数表达式.
(2)求第一班车从入口处到达塔林所需的时间.
(3)小聪在塔林游玩40分钟后,想坐班车到草甸,则小聪最早能够坐上第几班车?如果他坐这班车到草甸,比他在塔林游玩结束后立即步行到草甸提早了几分钟?(假设每一班车速度均相同,小聪步行速度不变)
【答案】(1);(2)第一班车从入口处到达塔林所需时间10分钟;(3)比他在塔林游玩结束后立即步行到草甸提早了7分钟
【详解】(1)由题意得,可设函数表达式为:,
把,代入,得,解得,
第一班车离入口处的路程(米与时间(分的函数表达为;
(2)把代入,解得,
(分,
第一班车从入口处到达塔林所需时间10分钟;
(3)设小聪坐上了第班车,则
,解得,
小聪坐上了第5班车,
等车的时间为5分钟,坐班车所需时间为:(分,
步行所需时间:(分,
(分,
比他在塔林游玩结束后立即步行到草甸提早了7分钟.
5.(2018•宁波)某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元.已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
(1)求甲、乙两种商品的每件进价;
(2)该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变.要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
【答案】(1)甲种商品的每件进价为40元,乙种商品的每件进价为48元;(2)甲种商品按原销售单价至少销售20件
【详解】(1)设甲种商品的每件进价为元,则乙种商品的每件进价为元.
根据题意,得,,
解得.
经检验,是原方程的解.
答:甲种商品的每件进价为40元,乙种商品的每件进价为48元;
(2)甲乙两种商品的销售量为.
设甲种商品按原销售单价销售件,则
,
解得.
答:甲种商品按原销售单价至少销售20件.
6.(2022•镇海区一模)要从甲、乙两仓库向,两工地运送水泥.已知甲仓库可运出100吨水泥,乙仓库可运出80吨水泥:工地需70吨水泥,工地需110吨水泥.设甲运往地的水泥为吨,两仓库到,两工地的运量和每吨的运费如表:
运量
运费(元吨)
甲仓库
乙仓库
甲仓库
乙仓库
地
24
18
地
25
16
(1)根据题意,完成表格;
(2)求出总运费关于的函数表达式;
(3)利用一次函数的增减性,求出的最小值.
【答案】(1)见解析;(2);(3)的最小值是3710
【详解】(1)由题意可得,
,两工地的运量和每吨的运费如表:
运量
运费(元吨)
甲仓库
乙仓库
甲仓库
乙仓库
地
24
18
地
25
16
故答案为:;,;
(2)由表格可得,
,
即总运费关于的函数表达式是;
(3),
随的增大而减小,
,
解得,
当时,取得最小值,此时,
答:的最小值是3710.
7.(2022•宁波模拟)甲、乙两地相距,一辆货车和一辆轿车先后从甲地出发驶向乙地(两车速度均保持不变).如图,折线表示轿车离甲地的距离(千米)与时间(小时)之间的函数关系,线段表示货车离甲地的距离(千米)与时间(小时)之间的函数关系,请你根据图象信息,解答下列问题:
(1)求轿车的速度和的值;
(2)求线段对应的函数表达式;
(3)轿车从甲地出发后经过多长时间追上货车?
【答案】(1)轿车的速度为120千米小时,的值是5.5;(2)线段对应的函数表达式是;(3)轿车从甲地出发后经过3.5小时追上货车
【详解】(1)由图可知,轿车的速度为(千米小时),,
答:轿车的速度为120千米小时,的值是5.5;
(2)设线段对应的函数表达式是,将,代入得:
,解得,
线段对应的函数表达式是;
(3)货车速度是(千米小时),
线段的函数表达式是,
由得,
,
答:轿车从甲地出发后经过3.5小时追上货车.
8.(2022•北仑区一模)甲、乙两地间的直线公路长为600千米,一辆轿车与一辆货车分别沿该公路从甲、乙两地以各自的速度相向而行,货车比轿车早出发1小时,途中轿车出现了故障,停下维修,货车仍继续行驶,1小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计)最后两车同时到达甲地,已知两车距各自出发地的距离(千米)与轿车所用的时间(小时)的关系如图所示,请结合图象解答下列问题:
(1)货车的速度是 千米时,的值是 ,轿车的速度是 千米时;
(2)求轿车距其出发地的距离(千米)与所用时间(小时)之间的函数表达式;
(3)求货车出发多长时间两车相距120千米.
【答案】(1)60,4,90;(2);(3)货车出发3.8小时或6小时时两车相距120千米
【详解】(1)由图象可得,
货车的速度为:(千米时),
,
轿车的速度为:(千米时),
故答案为:60,4,90;
(2)当时,设轿车距其出发地的距离(千米)与所用时间(小时)之间的函数表达式是,
点在该函数图象上,
,
解得,
即当时,轿车距其出发地的距离(千米)与所用时间(小时)之间的函数表达式是;
当时,;
当时,设轿车距其出发地的距离(千米)与所用时间(小时)之间的函数表达式是,
点,在该函数图象上,
,
解得,
即当时,轿车距其出发地的距离(千米)与所用时间(小时)之间的函数表达式是,
由上可得,轿车距其出发地的距离(千米)与所用时间(小时)之间的函数表达式是;
(3)设货车出发小时时两车相距120千米,
两车相遇之前:,
解得,
,
时符合题意;
两车相遇之后且轿车维修好之前:,
解得,
,
不符合题意,
,
解得,
当时,,此时轿车刚刚维修好,符合题意;
轿车维修好之后:由上可知,当货车行驶6小时时,两车相距120千米,又因为轿车速度大于货车速度,故两车越来越近,距离不可能是120千米;
由上可得,货车出发3.8小时或6小时时两车相距120千米.
9.(2022•宁波模拟)已知,两地之间有一条长240千米的公路.甲车从地出发匀速开往地,甲车出发半小时后,乙车从地出发沿同一路线匀速追赶甲车,两车相遇后,乙车原路原速返回地.两车之间的距离(千米)与甲车行驶时间(小时)之间的函数关系如图所示,请解答下列问题:
(1)甲车的速度是 千米时,乙车的速度是 千米时, .
(2)求乙车返回过程中,与之间的函数关系式.
(3)当甲、乙两车相距160千米时,直接写出甲车的行驶时间.
【答案】(1)60,80,3.5;(2)乙车返回过程中,与之间的函数关系式是;(3)当甲、乙两车相距160千米时,甲车的行驶时间是小时
【详解】(1)由图象可得,
甲车的速度为:(千米时),
乙车的速度为:(千米时),
,
故答案为:60,80,3.5;
(2)当时,,
设乙车返回过程中,与之间的函数关系式是,
点,在该函数图象上,
,
解得,
即乙车返回过程中,与之间的函数关系式是;
(3)当时,,
解得,
答:当甲、乙两车相距160千米时,甲车的行驶时间是小时.
10.(2022•宁波一模)小明4岁生日那天父亲种下一棵山毛榉和一棵枫树.当时测得山毛榉高为2.4米,枫树高为0.9米,小明6岁生日那天,测得山毛榉高为2.7米,枫树高为1.5米,现在枫树已经比山毛榉高了,在此期间,山毛榉的高度(米和枫树的高度(米与时间(年的函数图象如图所示,请结合图象信息解答下列问题:
(1)分别求出、与之间的函数表达式;
(2)估计小明现在的年龄应超过多少岁?
【答案】(1),;(2)至少经过10年枫树已经比山毛榉高,即小明的年龄应超过14岁
【详解】(1)由函数图象可知、是关于的一次函数,所以设,,
经过、,
,
解得,
;
经过、,
,
解得,
.
,.
(2)现在枫树已经比山毛榉高,
,
解得.
至少经过10年枫树已经比山毛榉高,即小明的年龄应超过14岁.
11.(2022•北仑区二模)如图1是一架菱形风筝,它的骨架由如图2的4条竹棒,,,组成,其中,,,分别是菱形四边的中点,现有一根长为的竹棒,正好锯成风筝的四条骨架,设,菱形的面积为.
(1)写出关于的函数关系式;
(2)为了使风筝在空中有较好的稳定性,要求,那么当骨架的长为多少时,这风筝即菱形的面积最大?此时最大面积为多少?
【答案】(1);(2)当即为时面积最大,此时最大面积为
【详解】(1)、为、中点,
.
同理:,
,
,
四边形是菱形,
.
(2),
,
,
,
.
又,
当即为时面积最大,此时最大面积为.
12.(2022•北仑区二模)新华书店决定用不多于28000元购进甲乙两种图书共1200本进行销售,已知甲种图书进价是乙种图书每本进价的1.4倍,若用1680元购进甲种图书的数量比用1400元购进的乙种图书的数量少10本.
(1)甲乙两种图书的进价分别为每本多少元?
(2)新华书店决定甲种图书售价为每本40元,乙种图书售价每本30元,问书店应如何进货才能获得最大利润?(购进的两种图书全部销售完)
【答案】(1)甲种图书进阶每本28元,乙种图书进阶每本20元;(2)书店甲种图书进货500本,乙种图书进货700本时利润最大,最大利润是13000元
【详解】(1)设乙种图书进阶每本元,则甲种图书进阶为每本元,
由题意得:,
解得:,
经检验,是原方程的解,且符合题意,
则,
答:甲种图书进阶每本28元,乙种图书进阶每本20元;
(2)设书店甲种图书进货本,总利润为元,
由题意得:,
,
解得:,
随的增大而增大,
当最大时最大,
当时,最大(元,
此时,乙种图书进货本数为(本
答:书店甲种图书进货500本,乙种图书进货700本时利润最大,最大利润是13000元.
13.(2022•鄞州区模拟)甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量(个与加工时间(分之间的函数关系,观察图象解决下列问题:
(1)点的坐标是 ,点表示的实际意义是 ;
(2)在加工的过程中,多少分钟时甲比乙多加工100个零件?
(3)为了使乙能与甲同时完成任务,现让丙帮乙一起加工,直到完成任务.已知丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第几分钟时开始帮助乙?并在图中画出丙帮助乙后与之间的函数关系的图象.
【答案】(1);甲乙两人工作15分钟时,加工零件的数量相同;(2)在加工的过程中,65分钟或125分钟时甲比乙多加工100个零件;(3)见解析
【详解】(1)点的坐标是,点表示的实际意义是:甲乙两人工作15分钟时,加工零件的数量相同,
故答案为:;甲乙两人工作15分钟时,加工零件的数量相同;
(2)①设的解析式为:,
把和代入得:,
解得:,
线段对应的函数关系式为:,
当时,,,
②由图形可知:甲因故障停止加工分钟后又继续按原速加工,
甲105分钟时,完成任务,即甲100分钟,加工600个零件,
甲加工的速度:,
设乙每分钟加工个零件,
,解得,
,
,又,
同理可得的函数表达式为:,
当时,,
解得,
综上所述,在加工的过程中,65分钟或125分钟时甲比乙多加工100个零件;
(3)设丙应在第分钟时开始帮助乙
分钟时,甲、乙加工零件的数量相同,
,
由题意得:,
解得,
丙应在第45分钟时开始帮助乙;
丙帮助后与之间的函数关系的图象如图:
14.(2022•海曙区一模)甲、乙两人从地前往地(途中经过地),甲骑摩托车,乙开汽车.已知甲比乙早出发2小时,全程未作停留:乙地发2小时后到达地,在地停留一段时间后继续行驶3小时后到达地,已知乙要比甲早到达地.设两车途中行驶速度不变,两车之间的距离(千米)与甲行驶的时间(小时)之间的函数关系如图所示.
(1)直接写出 , , ;
(2)已知,求甲的速度和乙的速度;
(3)在(2)的情况下,求甲从地到地这段路时与的函数关系式.
【答案】(1)2,4,;(2)甲的速度是40千米时,乙的速度是100千米时;(3)
【详解】(1)由题意得,点表示甲早出发2小时行驶的路程,故,
点表示乙出发2小时到达地,故,
甲全程用时12.5小时,乙全程用时5小时,故,
故答案为:2,4,;
(2)若,则,
设甲的速度是千米时,则乙的速度是千米时,
由题意得,,解得,
所以,,
答:甲的速度是40千米时,乙的速度是100千米时;
(3)如图,
点表示甲到达地,当时,甲到达地所用时间为,
,即,
由乙继续行驶3行驶到达地,可得,
所以当时,设,,
解得,
所以;
当时,设,
解得,
所以.
所以与的关系式为.
15.(2022•宁波模拟)一艘轮船在航行中遇到暗礁,船身有一处出现进水现象,等到发现时,船内已有一定积水,船员立即开始自救,一边排水一边修船,修船过程中进水和排水速度不变,修船完工后船不再进水,此时的排水速度与修船过程中进水速度相同,直到将船内积水排尽.设轮船触礁后船舱内积水量为,时间为,与之间的函数图象如图所示.
(1)修船过程中排水速度为 ,的值为 .
(2)求修船完工后与之间的函数关系式,并写出自变量的取值范围.
(3)当船内积水量是船内最高积水量的时,直接写出的值.
【答案】(1)1;24;(2);(3)或
【详解】(1)由题意可知,修船共用了:(分钟),
修船过程中进水速度为:(吨分钟),
修船过程中,排水速度是(吨分钟),
修船完工后船不再进水,此时的排水速度与修船过程中进水速度相同,
修船完工后,排水速度是,
;
故答案为:1;24;
(2)设修船完工后与之间的函数关系式为,
由题意,得,
解得,
修船完工后与之间的函数关系式为;
(3)在修船过程中,当船内积水量是船内最高积水量的时,可得,
解得;
修船完工后,当船内积水量是船内最高积水量的时,可得,
解得.
故的值为或.
16.(2022•海曙区校级一模)一辆轿车从宁波开往杭州,一辆货车从杭州开往宁波,两车同时出发,分别以各自的速度在同一条高速路上匀速行驶分钟后,轿车司机发现有重要文件遗忘在宁波,便立即返回取得文件后再从宁波开往杭州(取文件时间忽略不计),结果轿车先到达杭州,货车继续行驶到宁波.设货车行驶时间为,两车之间的距离为,与的函数图象如图所示,请回答下列问题:
(1)求两车的速度.
(2)说明点所表示的实际意义.
(3)求直线的函数解析式.
【答案】(1)货车速度是,轿车速度为;(2)点所表示的实际意义是出发后两车小时相遇;(3)
【详解】(1)由图可知,货车2小时行驶160千米,
货车速度是,
两车速度和为,
轿车速度为;
答:货车速度是,轿车速度为;
(2)设出发后两车小时相遇,
根据题意得:,
解得,
,,
点所表示的实际意义是出发后两车小时相遇;
(3)轿车到达杭州所用时间为,
轿车到达杭州时货车行驶路程是,
,,
设直线的函数解析式为,把,,,代入得:
,解得,
直线的函数解析式为.
17.(2022•鄞州区校级一模)今年以来,东钱湖旅游市场迎来复苏,接待的游客人数逐月增加,据统计,游玩东钱湖景区的游客人数一月份为30万人次,三月份为43.2万人次.
(1)求二月和三月这两个月中,东钱湖景区游客人数平均每月的增长率;
(2)位于东钱湖的福泉山、陶公岛景点需购票游览,售票处出示的三种购票方式如下:
方式1:只购买陶公岛景点,30元人;
方式2:只购买福泉山景点,50元人;
方式3:陶公岛和福泉山联票,76元人.
预测,四月份选择这三种购票方式的人数分别有2万、1万和1万,为增加收入,对门票价格进行调整,发现当方式1和2的门票价格不变时,方式3的联票价格每下降1元,将有原计划只购买陶公岛门票的400人和原计划只购买福泉山门票的600人改为购买联票.
①联票价格下降5元,请通过计算预测四月份的门票总收入;
②请问:当联票价格下降多少元时,四月份的门票总收入最大?最大值是多少万元?
【答案】(1)每月的增长率为;(2)①(万元);②当联票价格下降12元时,四月份的门票总收入最大,最大值是200.4万元
【详解】(1)设每月的增长率为,
由题意得,,
解得,(舍去),
答:每月的增长率为;
(2)①当联票价格下降5元,方式1的收入为(万元),
方式2的收入为(万元),
方式3的收入为(万元),
所以四月份的门票总收入为(万元);
②设联票价格下降元,四月份的门票总收入为万元,
由题意得,.
,
当时,最大为200.4,
答:当联票价格下降12元时,四月份的门票总收入最大,最大值是200.4万元.
18.(2022•镇海区校级模拟)2021年12月5日,镇海区爆发新冠疫情,广大居民捐资捐物,经过全区人民的共同努力,镇海区用两周的时间解除了疫情.某商店也将商品两周的盈利捐出用于购买抗疫物资.经市场调查发现,该商品的周销售量(件关于售价(元件)的一次函数为,当售价为40元时,周销售利润为2400元.
(1)该商品每件的进价是多少元?
(2)当每件售价为多少时,周售价利润最大?并求出此时的最大利润.
【答案】(1)每件商品的进价20元;(2)当每件售价为60元时,周售价利润最大,最大利润是3200元
【详解】(1)把代入可得,
(元,
所以每件商品的进价20元;
(2)设利润为元,则,
,
当时,最大为3200,
答:当每件售价为60元时,周售价利润最大,最大利润是3200元.
19.(2022•宁波模拟)某电子公司前期投入240万元作为某种电子产品的研发费用,成功研制出这种市场热销的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为8元件,在销售过程中发现:每年的年销售量(万件)与销售价格(元件)的关系如图所示.设该电子公司销售这种电子产品的年利润为(万元).(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本)
(1)请求(万件)与销售价格(元件)之间的出函数关系式;
(2)求出第一年这种电子产品的年利润(万元)与销售价格(元件)之间的出函数关系式,并求出第一年年利润的最大值(第一年年利润总售价总成本研发费用);
(3)假设公司的这种电子产品第一年恰好按年利润(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种电子产品每件的销售价格定在12元以上,若年销售量与每件销售价格仍满足(1)的关系,当第二年的年利润不低于44万元时,求出第二年销售量的最大值.
【答案】(1);(2),第一年年利润的最大值时万元;(3)当第二年的年利润不低于44万元时,第二年销售量的最大值是14万件
【详解】(1)设(万件)与销售价格(元件)之间的函数关系式是,将,代入得:
,
解得,
;
(2)根据题意得:,
,
时,取最大值,最大值为,
答:,第一年年利润的最大值时万元;
(3)第一年的年利润为万元,
万元应作为第二年的成本,
第二年的年利润,
令,则,
解得,,
时,第二年的年利润不低于44万元,
,
随的增大而减小,
时,有最大值,最大值为,
当第二年的年利润不低于44万元时,第二年销售量的最大值是14万件.
20.(2022•宁波模拟)小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,如图是她本次去舅舅家所用的时间与小红离家的距离的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是 米,小红在商店停留了 分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快?最快的速度是多少米分?
(3)本次去舅舅家的行程中,小红一共行驶了多少米?
【答案】(1)1500,4;(2)小红在分钟最快,速度为(米分);(3)本次去舅舅家的行程中,小红一共行驶了:(米)
【详解】(1)根据图象舅舅家纵坐标为1500,小红家的纵坐标为0,故小红家到舅舅家的路程是1500米;据题意,小红在商店停留的时间为从8分到12分,故小红在商店停留了4分钟.
故答案为:1500,4;
(2)根据图象,时,直线最陡,
故小红在分钟最快,速度为(米分);
(3)本次去舅舅家的行程中,小红一共行驶了:(米).
21.(2022•鄞州区一模)如图是一次药物临床试验中受试者服药后血液中的药物浓度(微克毫升)与用药的时间(小时)变化的图象.第一次服药后对应的图象由线段和部分双曲线组成,服药6小时后血液中的药物浓度达到最高,16小时后开始第二次服药,服药后对应的图象由线段和部分曲线组成,其中与平行,血液中的浓度不低于5微克毫升时有疗效.
(1)分别求受试者第16小时,第22小时血液中的药物浓度;
(2)受试者第一次服药后第二次服药前这16小时内,有疗效的持续时间达到6小时吗?
(3)若血液中的药物浓度不高于4微克毫升时才能进行第三次服药,问受试者第二次服药后至少经过几小时可进行第三次服药?
【答案】(1)第16小时血液中的药物浓度为3微克毫升,第22小时血液中的药物浓度为11微克毫升;
(2)有疗效的持续时间未达到6小时;(3)受试者第二次服药后至少经过48小时可进行第三次服药
【详解】(1)将点代入,
得,
,
当时,,
,
设的解析式:,
代入,
得,
解得,
的解析式:,
与平行,
设的解析式:,
代入,
得,
解得,
的解析式:,
当时,,
,
第16小时血液中的药物浓度为3微克毫升,第22小时血液中的药物浓度为11微克毫升;
(2)当,解得,
当,解得,
,
有疗效的持续时间未达到6小时;
(3)将点代入,
得,
解得,
段函数解析式:,
当时,,
(小时),
受试者第二次服药后至少经过48小时可进行第三次服药.
22.(2022•慈溪市一模)甲、乙两人沿同一路线从地到地进行骑车训练,甲先出发,匀速骑行到地.乙后出发,并在甲骑行25分钟后提速到原来速度的1.4倍继续骑行(提速过程的时间忽略不计),结果乙比甲早2分钟到地.两人距离地的路程(单位:千米)与甲骑行的时间(单位:分钟)之间的关系如图所示.
(1)求甲的速度和乙提速前的速度.
(2)求两地之间的路程.
【答案】(1)乙提速前的速度为分钟;(2)
【详解】(1)由题意得:甲的速度为分钟,
设乙提速前的速度为,则,
解得分钟,
乙提速前的速度为分钟.
(2)乙提速前的速度为分钟,
乙提速后的速度为分钟,
乙提速前行驶路程为,
设两地之间的路程为,则,
解得.
两地之间的路程为.
23.(2022•镇海区二模)4月23日是“世界界读书日”,宁波某学校为了更好地营造读书好、好读书、读好书的书香校园.学校图书馆决定去选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果学校图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该学校图书馆最多可以购买甲和乙图书共多少本?
【答案】(1)甲图书每本价格是50元,乙图书每本价格为20元;(2)该学校图书馆最多可以购买甲和乙图书共38本
【详解】(1)设乙图书每本价格为元,则甲图书每本价格是元,
根据题意得:,
解得:,
经检验得:是原方程的根,
则,
答:甲图书每本价格是50元,乙图书每本价格为20元;
(2)设购买甲种图书本,则购买乙种图书本,
由(1)知,乙种图书每本20元,甲种图书每本50元,
由题意得:,
解得:,
,
则,
答:该学校图书馆最多可以购买甲和乙图书共38本.
24.(2022•余姚市一模)“一方有难,八方支援”.疫情期间,某志愿者组织筹集两车物资送往疫情严重地区.图中的折线、线段分别表示甲,乙两车所走的路程(千米),(千米)与时间(小时)之间的函数关系对应的图象.
请根据图象所提供的信息,解决下列问题:
(1)乙车的速度为 千米小时,甲车由于发生故障,在途中停留了 小时.
(2)甲车排除故障后立即提速10千米小时赶往目的地,求甲车原来的速度.
(3)排除故障后甲车与乙车第一次相遇时,距出发点的路程为多少千米?
【答案】(1)65;1;(2)甲车原来的速度为80千米小时;(3)排除故障后甲车与乙车第一次相遇时,距出发点的路程为286千米
【详解】(1)由题意,得乙车的速度为:(千米小时),甲组在途中停留时间为:(小时),
故答案为:65;1;
(2)设甲车原来的速度为千米小时,根据题意得:
,
解得,
答:甲车原来的速度为80千米小时;
(3)设排除故障后甲车与乙车第一次相遇时的时间为小时,根据题意得:
,
解得,
(千米),
答:排除故障后甲车与乙车第一次相遇时,距出发点的路程为286千米.
25.(2022•江北区模拟)在一次自行车越野赛中,甲乙两名选手行驶的路程(千米)随时间(分变化的图象(全程)如图,解决下列问题,
(1)求线段所在的直线函数表达式;
(2)求两人第一次相遇时,行驶的时间;
(3)求这次越野赛的全程是多少;
(4)两人第二次相遇时,行驶了多长时间?
【答案】(1)线段所在的直线函数表达式为;(2)两人第一次相遇时,行驶的时间是48分钟;(3)这次越野赛的全程是;(4)两人第二次相遇时,行驶了76分钟
【详解】(1)设线段所在的直线函数表达式为,将,代入得:
,
解得,
线段所在的直线函数表达式为;
(2)在中,令得:
,
解得,
答:两人第一次相遇时,行驶的时间是48分钟;
(3)由(2)可知,乙用48分钟行驶了,
这次越野赛的全程是,
答:这次越野赛的全程是;
(4)由(3)知,
,
直线的解析式为,
由,得直线解析式为,
解得,
答:两人第二次相遇时,行驶了76分钟.
26.(2022•宁波模拟)已知,两地相距256千米.早上9点甲车从地出发去地,20分钟后,乙车从地出发去地.两车离开各自出发地的路程(千米)与时间(小时)的函数关系如图所示.
(1)求乙车的与的函数关系式;
(2)几时几分两人相遇?相遇时离地的路程多少?
【答案】(1);(2)时两人相遇,相遇时离地的路程为140.8千米
【详解】(1)甲车的函数图象过点,且为正比例函数,所以函数关系式为,
当时,,
乙车的函数图象过点,,,
设其函数关系式为,
则,
解得,
;
(2)由题意得:,
解得,
1.8小时分钟,所以两车在时相遇,
此时,
答:时两人相遇,相遇时离地的路程为140.8千米.
27.(2022•宁波模拟)“5,12”汶川大地震后,某药业生产厂家为支援灾区人民,准备捐赠320箱某种急需药品,该厂家备有多辆甲、乙两种型号的货车,如果单独用甲型号车若干辆,则装满每车后还余20箱未装;如果单独用同样辆数的乙型号车装,则装完后还可以再装30箱,已知装满时,每辆甲型号车比乙型号车少装10箱.
(1)求甲、乙两型号车每辆车装满时,各能装多少箱药品?
(2)已知将这批药品从厂家运到灾区,甲、乙两型号车的运输成本分别为400元辆和430元辆.设派出甲型号车辆,乙型号车辆时,运输的总成本为元,请你提出一个派车方案,保证320箱药品装完,且运输总成本最低,并求出这个最低运输成本为多少元?
【答案】(1)甲型号车能装60箱药品,乙型号车能装70箱药品;(2)这个最低运输成本为2060元
【详解】(1)设甲型号车装满为箱,则乙型号车装满为箱.
由题意得:.
解之得:.
经检验:是原方程的解.
箱.
答:甲型号车能装60箱药品,乙型号车能装70箱药品.
(2),.
派车预设方案如下:
甲车(辆)
甲车辆成本
乙车(辆)
乙车辆成本
总成本(元)
6
2400
0
0
2400
5
2000
1
430
2430
4
1600
2
860
2460
3
1200
2
860
2060
2
800
3
1290
2090
1
400
4
1720
2120
0
0
5
2150
2150
从上表得出:派出甲型号车辆,乙型号车辆时,运输的总成本最低.
且(元.
这个最低运输成本为2060元.
28.(2022•宁波模拟)周末,自行车骑行爱好者甲、乙两人相约沿同一路线从地出发前往地进行骑行训练,甲、乙分别以不同的速度匀速骑行,乙比甲早出发5分钟.乙骑行25分钟后,甲以原速的继续骑行,经过一段时间,甲先到达地,乙一直保持原速前往地.在此过程中,甲、乙两人相距的路程(单位:米)与乙骑行的时间(单位:分钟)之间的关系如图所示.
(1)求甲、乙两人出发时的速度分别为多少米分?
(2)甲、乙两人相遇时,甲出发了几分钟?
(3)乙比甲晚几分钟到达地?
【答案】(1)甲出发时速度是250米分,乙出发时速度是300米分;(2)甲出发了45分钟;(3)乙比甲晚12分钟到达地
【详解】(1)由题意得,乙的速度为(米分),
设甲的速度为米分.则有:
,
解得,
答:甲出发时速度是250米分,乙出发时速度是300米分;
(2)25分钟后甲的速度为(米分),
(分,
(分,
答:甲出发了45分钟;
(3)由题意得,总里程(米,
86分钟乙的路程为(米,
(分钟).
答:乙比甲晚12分钟到达地.
29.(2020•义乌市模拟)新冠肺炎期间,某超市将购进一批口罩进行销售,已知购进4盒甲口罩和6盒乙口罩需260元,购进5盒甲口罩和4盒乙口罩需220元.两种口罩以相同的售价销售,甲口罩的销量(盒)与售价(元之间的关系为;当售价为40元时,乙口罩可销售100盒,售价每提高1元,少销售5盒.
(1)求甲、乙两种口罩每盒的进价分别为多少元?
(2)当乙口罩的售价为多少元时,乙口罩的销售总利润最大?此时两种口罩的销售利润总和为多少?
(3)已知甲的销售量不低于乙口罩的销售量的,若使两种口罩的利润总和最高,此时的定价应为多少?
【答案】(1)甲、乙两种口罩每盒的进价分别为20元、30元;(2)当乙口罩的售价为45元时,乙口罩的销售总利润最大,此时两种口罩的销售利润总和为2125元;(3)若使两种口罩的利润总和最高,此时的定价应为36元
【详解】(1)设甲、乙两种口罩每盒的进价分别为元、元,由题意得:
,
解得:.
甲、乙两种口罩每盒的进价分别为20元、30元.
(2)设乙口罩的销售利润为元,由题意得:
,
当乙口罩的售价为45元时,乙口罩的销售总利润最大,为1125元.
当售价为45元时,(盒;
甲口罩的销售利润为:(元,
此时两种口罩的销售利润总和为:(元.
当乙口罩的售价为45元时,乙口罩的销售总利润最大,此时两种口罩的销售利润总和为2125元.
(3)由题意得:,
解得:,
两种口罩的利润总和
,
对称轴为:,
当时,两种口罩的利润总和最高.
若使两种口罩的利润总和最高,此时的定价应为36元.
30.(2022•鄞州区模拟)某风景区内的公路如图1所示,景区内有免费的班车,从入口处出发,沿该公路开往草甸,途中停靠塔林(上下车时间忽略不计).第一班车上午8点发车,以后每隔10分钟有一班车从入口处发车.小聪周末到该风景区游玩,上午到达入口处,因还没到班车发车时间,于是从景区入口处出发,沿该公路步行25分钟后到达塔林.离入口处的路程(米与时间(分的函数关系如图2所示.
(1)求第一班车离入口处的路程(米与时间(分的函数表达式.
(2)求第一班车从入口处到达塔林所需的时间.
(3)小聪想在塔林坐第四辆班车到草甸,则小聪最多能在塔林玩多少分钟?(假设每一班车速度均相同,小聪从塔林步行到车站的时间忽略不计)
【答案】(1)第一班车离入口处的路程(米与时间(分的函数表达为;
(2)第一班车从入口处到达塔林所需时间10分钟;(3)小聪最多能在塔林玩35分钟
【详解】(1)由题意得,可设函数表达式为:,
把,代入,
得,
解得:,
第一班车离入口处的路程(米与时间(分的函数表达为;
(2)把代入,解得,
(分,
第一班车从入口处到达塔林所需时间10分钟;
(3)由题意得:(分钟),
小聪最多能在塔林玩35分钟.
31.(2022•海曙区校级模拟),两地相距290千米,早上货车甲从地出发将一批物资运往地,行驶一段路程后出现故障,即刻停车与地联系.地收到消息后立即派货车乙从地出发去接运甲车上的物资,货车乙到甲后,用了30分钟将物资从货车甲搬运到货车乙上,随后开往地,两辆货车离开各自出发地的路程(千米)与时间(时的函数关系如图所示.(通话等其他时间忽略不计)
(1)直接写出货车甲,货车乙(相遇前)的速度.
(2)求货车乙在未遇到货车甲时,它离开出发地的路程(千米)与时间(时的函数表达式.
(3)因实际需要,要求货车乙到达地的时间比货车甲按原来的速度正常到达地的时间最多晚1个小时,问货车乙返回地的速度至少为每小时多少千米?
【答案】(1)货车甲出发时的速度是:60(千米小时),货车乙的速度是:100(千米小时);(2);(3)货车乙返回地的车速至少为千米小时
【详解】(1)货车甲出发时的速度是:(千米小时),货车乙的速度是:(千米小时),
(2)设函数表达式为,
把,代入,得:
,
解得,
;
(3)当时,
,
解得,
由(1)可知甲的速度为60千米小时,
货车甲正常到达地的时间为(小时),
(小时),(小时),(小时),
设货车乙返回地的车速为千米小时,
,
解得.
答:货车乙返回地的车速至少为千米小时.
32.(2022•海曙区校级三模)端午节是我们中华民族的传统节日,某校九年级1班准备在端午节当天组织学生包粽子.班级分为男生(甲女生(乙两个小组,甲组男生在包粽子过程中因体育锻炼暂停一会,然后以原来的工作效率继续包粽子,由于时间紧任务重,乙组女生也加入共同加工粽子.设甲组男生加工时间(分钟),甲组加工粽子的数量为(个,乙组女生加工粽子的数量为(个,其函数图象如图所示.
(1)求与之间的函数关系式,并写出的取值范围;
(2)求的值,并说明的实际意义;
(3)甲组男生加工多长时间时,甲、乙两组加工粽子的总数为480个?直接写出答案.
【答案】(1);(2)的值是280,实际意义是当男生包粽子80分钟时,一共包粽子280个;(3)甲组男生加工70分钟时,甲、乙两组加工粽子的总数为480个
【详解】(1)设与之间的函数关系式是,
则,
解得,
即与之间的函数关系式是;
(2)由图象可得,
男生包粽子的速度为(个分钟),
,
即的值是280,实际意义是当男生包粽子80分钟时,一共包粽子280个;
(3)由题意可得,当时,由于工作效率没有变,
,
当时,
,
得,
甲组男生加工70分钟时,甲、乙两组加工粽子的总数为480个.
专题18 几何压轴题-备战宁波中考数学真题模拟题分类汇编: 这是一份专题18 几何压轴题-备战宁波中考数学真题模拟题分类汇编,文件包含专题18几何压轴题-备战宁波中考数学真题模拟题分类汇编解析版docx、专题18几何压轴题-备战宁波中考数学真题模拟题分类汇编原卷版docx等2份试卷配套教学资源,其中试卷共103页, 欢迎下载使用。
专题16 解三角形综合题-备战宁波中考数学真题模拟题分类汇编: 这是一份专题16 解三角形综合题-备战宁波中考数学真题模拟题分类汇编,文件包含专题16解三角形综合题-备战宁波中考数学真题模拟题分类汇编解析版docx、专题16解三角形综合题-备战宁波中考数学真题模拟题分类汇编原卷版docx等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。
专题14 概率统计综合题-备战宁波中考数学真题模拟题分类汇编: 这是一份专题14 概率统计综合题-备战宁波中考数学真题模拟题分类汇编,文件包含专题14概率统计综合题-备战宁波中考数学真题模拟题分类汇编解析版docx、专题14概率统计综合题-备战宁波中考数学真题模拟题分类汇编原卷版docx等2份试卷配套教学资源,其中试卷共54页, 欢迎下载使用。












