2023年辽宁省凤城市中考一模数学试题（含答案）

2023年成绩监测

九年级数学试卷

考试时间：120分钟 试卷满分：150分

第一部分  客观题（请用2B铅笔将正确答案涂在答题卡对应的位置上）

一、选择题（每小题3分，共30分）下列各题的备选答案中，只有一个是正确的，请将正确答案涂在答题卡上．

1．若一个数的相反数是5，则这个数是（    ）

A．5 B．0或5 C． D．-5

2．下列计算正确的是（    ）

A．  B．

C．  D．

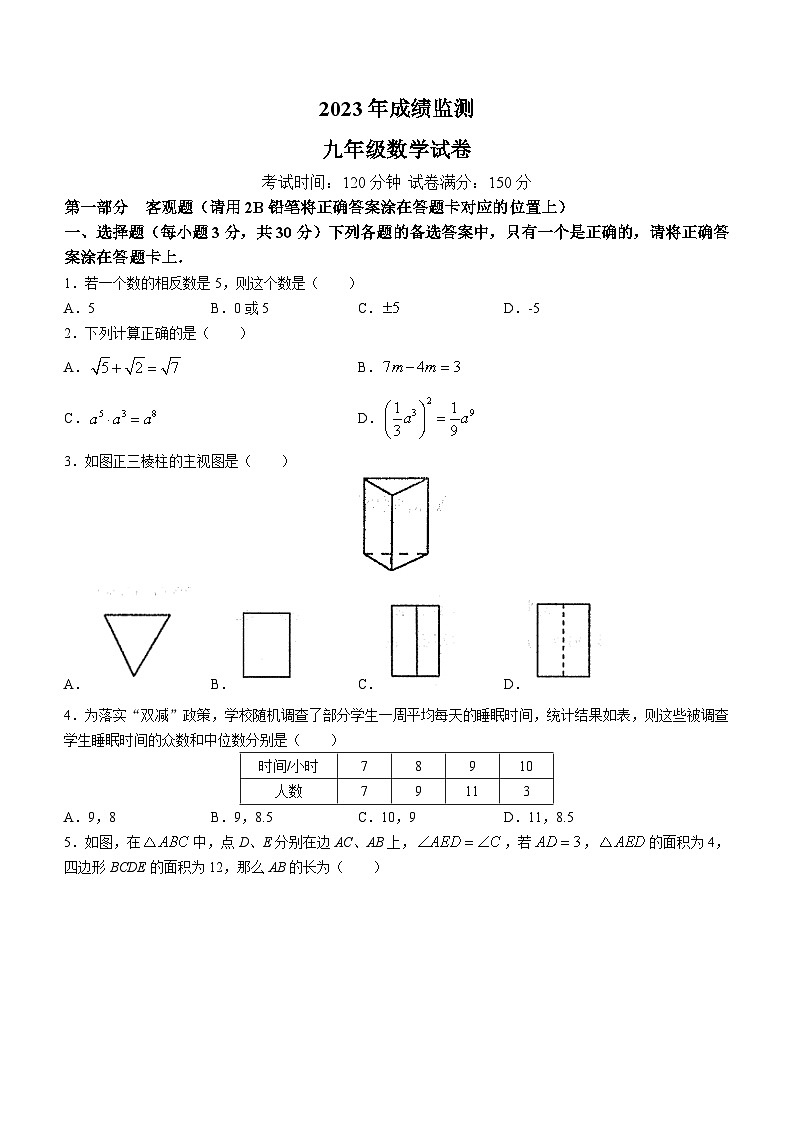
3．如图正三棱柱的主视图是（    ）

A． B． C． D．

4．为落实“双减”政策，学校随机调查了部分学生一周平均每天的睡眠时间，统计结果如表，则这些被调查学生睡眠时间的众数和中位数分别是（    ）

A．9，8 B．9，8.5 C．10，9 D．11，8.5

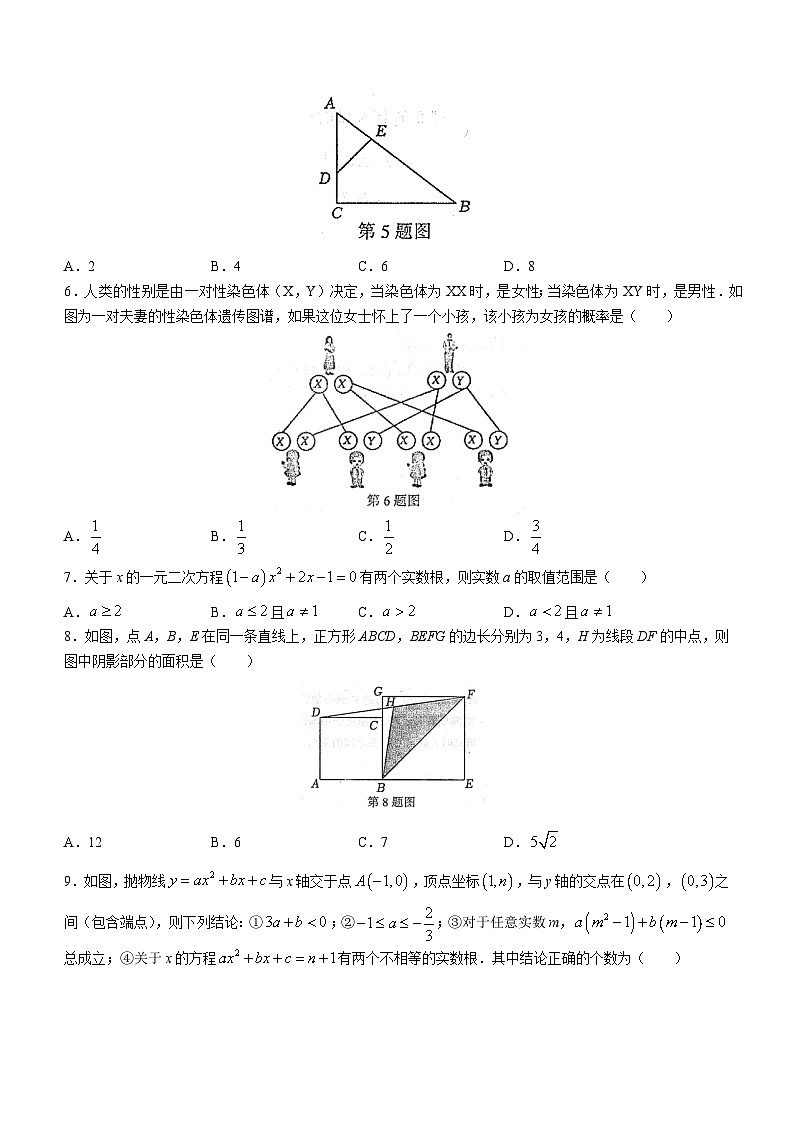
5．如图，在中，点D、E分别在边AC、AB上，，若，的面积为4，四边形BCDE的面积为12，那么AB的长为（    ）

A．2 B．4 C．6 D．8

6．人类的性别是由一对性染色体（X，Y）决定，当染色体为XX时，是女性；当染色体为XY时，是男性．如图为一对夫妻的性染色体遗传图谱，如果这位女士怀上了一个小孩，该小孩为女孩的概率是（    ）

A． B． C． D．

7．关于x的一元二次方程有两个实数根，则实数a的取值范围是（    ）

A． B．且 C． D．且

8．如图，点A，B，E在同一条直线上，正方形ABCD，BEFG的边长分别为3，4，H为线段DF的中点，则图中阴影部分的面积是（    ）

A．12 B．6 C．7 D．

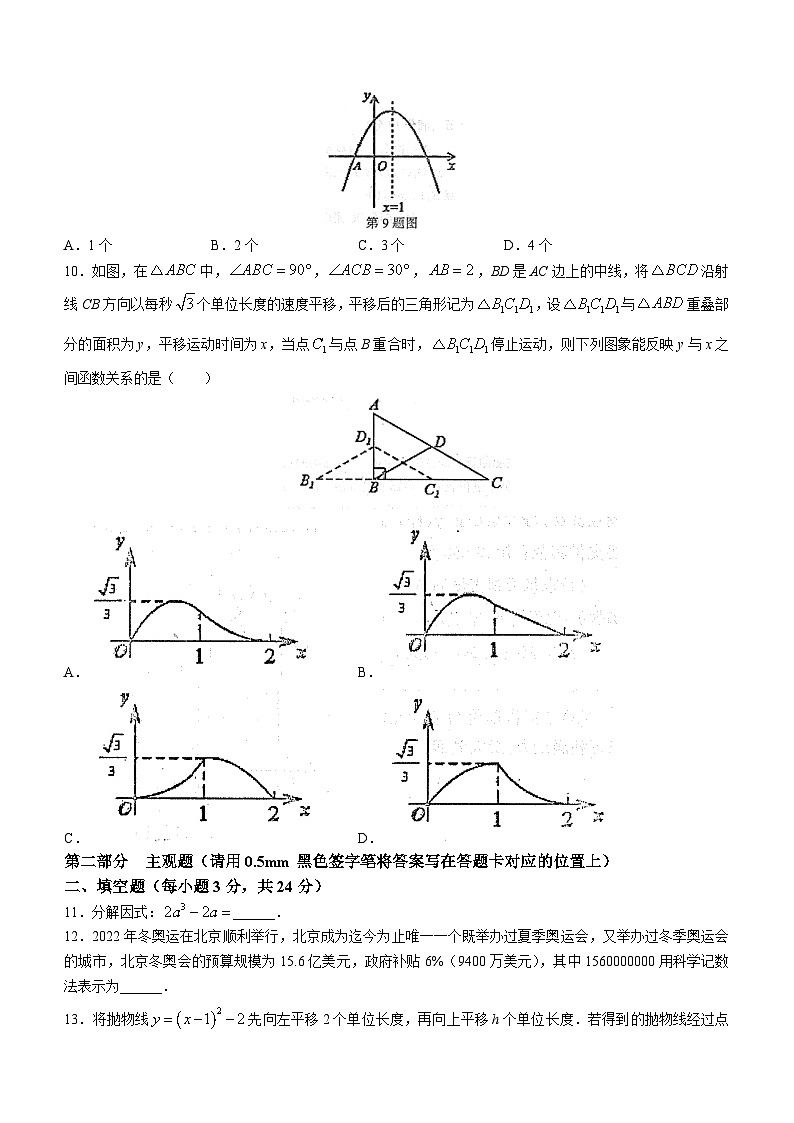
9．如图，抛物线与x轴交于点，顶点坐标，与y轴的交点在，之间（包含端点），则下列结论：①；②；③对于任意实数m，总成立；④关于x的方程有两个不相等的实数根．其中结论正确的个数为（    ）

A．1个 B．2个 C．3个 D．4个

10．如图，在中，，，，BD是AC边上的中线，将沿射线CB方向以每秒个单位长度的速度平移，平移后的三角形记为，设与重叠部分的面积为y，平移运动时间为x，当点与点B重合时，停止运动，则下列图象能反映y与x之间函数关系的是（    ）

A． B．

C． D．

第二部分  主观题（请用0.5mm黑色签字笔将答案写在答题卡对应的位置上）

二、填空题（每小题3分，共24分）

11．分解因式：______．

12．2022年冬奥运在北京顺利举行，北京成为迄今为止唯一一个既举办过夏季奥运会，又举办过冬季奥运会的城市，北京冬奥会的预算规模为15.6亿美元，政府补贴6%（9400万美元），其中1560000000用科学记数法表示为______．

13．将抛物线先向左平移2个单位长度，再向上平移h个单位长度．若得到的抛物线经过点，则h的值是______．

14．一个不透明的布袋里装有2个白球，1个黑球和若干个红球，它们除颜色外其余都相同，每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定于，由此可估计袋中约有红球______个．

15．如图，矩形AEFG的顶点E、F分别在菱形ABCD的边AB和对角线BD上，连接EG、CF，若，则CF的长为______．

16．如图，在平面直角坐标系中，点O为坐标原点，在第一象限，边OA在x轴上，反比例函数的图象过点C，的图象经过点B，若，则k的值为______．

17．如图，在矩形纸片ABCD中，，点E是AB的中点，点F是AD边上的一个动点，将沿EF所在直线翻折，得到，连接，，则当是以为腰的等腰三角形时，FD的长是______．

18．如图，和都是等腰直角三角形，，点D是BC边上的动点（不与点B、C重合），DE与AC交于点F，连结CE．下列结论：①；②；③若，则；④在内存在唯一一点P，使得的值最小，若点D在AP的延长线上，且AP的长为2，则．其中含所有正确结论的选项是______．

三、解答题（第19题8分，第20题14分，共22分）

19．先化简，再求值：，其中．

20．我市为加快推进生活垃圾分类工作，对分类垃圾桶实行统一的外型、型号、颜色等，其中，可回收物用蓝色收集桶，有害垃圾用红色收集桶，厨余垃圾用绿色收集桶，其他垃圾用灰色收集桶．为了解学生对垃圾分类知识的掌握情况，某校宣传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生，根据调查结果，绘制了如图所示的两幅不完整的统计图．

根据图中信息，解答下列问题：

（1）此次调查一共随机采访了______名学生，在扇形统计图中，“灰”所在扇形的圆心角的度数为______度；

（2）补全条形统计图（要求在条形图上方注明人数）；

（3）若该校有3600名学生，估计该校学生将用过的餐巾纸投放到红色收集桶的人数；

（4）李老师计划从A，B，C，D四位学生中随机抽取两人参加学校的垃圾分类知识抢答赛，请用树状图法或列表法求出恰好抽中A，B两人的概率．

四、（每题12分，共24分）

21．为有效落实双减工作，切实做到减负提质，很多学校决定在课后看护中增加乒乓球项目．体育用品商店得知后，第一次用600元购进乒乓球若干盒，第二次又用600元购进乒乓球若干盒，但这次每盒的进价是第一次进价的倍，购进数量比第一次少了30盒，求第一次每盒乒乓球的进价是多少元？

22．如图，某海岸边有B，C两码头，C码头位于B码头的正东方向，距B码头40海里，甲乙两船同时从A岛出发，甲船向位于A岛正北方向的B码头航行，乙船向位于A岛北偏东30°方向的C码头航行，当甲船到达距B码头30海里的E处时，乙船位于甲船北偏东60°方向的D处，求此时乙船与C码头之间的距离．（结果保留根号）

五、（满分12分）

23．如图，在中，，AD平分交BC于点D，O为AB上一点，经过点A，D的分别交AB，AC于点E，F，连接DF．

（1）求证：BC是的切线；

（2）连接DE，求证：；

（3）若，，求AD的长．

六、（满分12分）

24．某商店购进了一批以欢度春节为主题的玩具饰品进行销售，玩具饰品的进价为每件30元，物价部门规定其每件的售价不低于进价且利润不高于进价的90%，根据市场调查发现，每天销售量y（件）与销售单价x（元）的关系如图所示，在销售过程中每天还要支付其他费用共850元．

（1）求每天销售量y（件）与销售单价x（元）的函数关系式，并写出自变量x的取值范围；

（2）求该批玩具的每天销售利润W（元）与销售单价x（元）的函数关系式；

（3）当销售单价为多少元时，该批玩具每天销售利润最大，最大利润为多少元？

七、（满分12分）

25．如图①，E在AB上，、都为等腰直角三角形，，连接DB，以DE、DB为边作平行四边形DBFE，连接FC、DC．

（1）求证：；；

（2）将图①中绕A点顺时针旋转，其它条件不变，如图②，（1）的结论是否成立？说明理由．

（3）将图①中的绕A点顺时针旋转，，其它条件不变，当四边

形DBFE为矩形时，直接写出的值．

八、（满分14分）

26．如图，在平面直角坐标系中，抛物线与坐标轴交于，两点，直线交y轴于点C．点E为直线AD上方抛物线上一动点，过点E作x轴的垂线，垂足为G，EG分别交直线AC，AD于点F，H．

（1）求抛物线的表达式；

（2）当时，连接AE，求的面积；

（3）Q是y轴上一点，当四边形AFQH是矩形时，请直接写出点Q的坐标；

（4）在（3）的条件下，第四象限有一动点P，满足，请求出周长的最小值．

九年级数学试卷参考答案及评分标准

2023年3月

（若有其它正确方法，请参照此标准赋分）

一、选择题（每小题3分，共30分）

二、填空题（每小题3分，共24分）

11． 12． 13．4 14．3

15．5 16．3 17．或 18．①②③

三、解答题（第19题8分，第20题14分，共22分）

19．解：

=

∵

∴原式

20．解：（1）200，198；

（2）（人）补全图形如下：

（3）估计该校学生用过的餐巾纸投放到红色收集桶的人数为：（人）

（4）列表如下：

由表格知，共有12种等可能结果，其中恰好抽中A，B两人的有2种结果．

所以恰好抽中A，B两人的概率为

四、（每题12分，共24分）

21．解：设第一次每盒乒乓球进价为x元，

则第二次每盒乒乓球进价为元，由题意得．

解得：，经检验：是原方程的解

答：第一次每盒乒乓球的进价是4元

22．解：过D作于F，

∵，∴，∴，

∵，，，∴，，

∵，∴．

在中，，

∴，

∵，∴，

∴

答：此时乙船与C码头之间的距离为海里

五、（满分12分）

23．（1）证明：连接OD，∵AD平分，

∴，∵，∴，

∴，∴，∵，∴

又∵OD是半径，∴BC是的切线

（2）∵，∴，

∵AE是直径，∴，

∴，∴

又∵，∴，

∴，∵，∴

（3）

六、（满分12分）

24．解：设每天销售量y（件）与销售单价x（元）的函数关系式为

∵点，在该函数图象上，

得，解得，

∴，∵售价不低于进价且利润不高于进价的90%，

故，即

（2）

（3）

∴图象开口向下，对称轴，∵

∴时，W取得最大值，此时

答：当销售单价为57元时，该批玩具每天销售利润最大，最大利润为2633元．

七、（满分12分）

25．（1）证明：：，都为等腰直角三角形

∴，，

∵四边形DBFE为平行四边形，∴，

∴，

∴

∵，∴

∴，∴，

∴，∴，

（2）结论成立，理由如下：

延长DE交BC于G，∵四边形DBFE为平行四边形

∴，∴，∵

∴

又∵，∴，

∵，，∴，

∴，，

∴，∴，

（3）45°或225°

八、（满分14分）

26．解：（1）∵抛物线过，两点，

∴；

（2）设AD的解析式为：，

∴，解得：，∴AD的解析式为：．

∵，∴把代入得，

于是得到，，∴的面积

（3）

（4）∵且，

∴的周长，

要使得的周长最小，只要的值最小，

∵，∴当点P在AC上时，的值最小，

∵，∴的周长的最小值为．