

贵州省2023届高三下学期3+3+3高考备考诊断性联考(三)数学(理)试卷(含答案)
展开贵州省2023届高三下学期3+3+3高考备考诊断性联考(三)数学(理)试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、在复平面内, 敀数 z对应的点的坐标为, 则 ( )
A. B. C. D.
2、,, 则 ( )
A. B.
C. D.
3、2023 年 “三月三”期间, 广西交通部门统计了 2023 年 4 月 19 日至 4 月 25 日的高速公路车 流量 (单位:万车次), 并与 2022 年比较, 得到同比增长率(同比增长率)数据, 绘制了如图 所示的统计图, 则下列结论错误 去年同期车流是的是( )
A. 2023 年 4 月 19 日至 4 月 25 日的高速公路车流量的极差为 23
B. 2023 年 4 月 19 日至 4 月 25 日的高速公路车流量的中位数为 17
C. 2023 年 4 月 19 日至 4 月 21 日的高速公路车流量的标准差小于 2023 年 4 月 23 日至 4月 25 日的高速公路车流量的标准差
D. 2022 年 4 月 23 日的离速公路车流量为 20 万车次
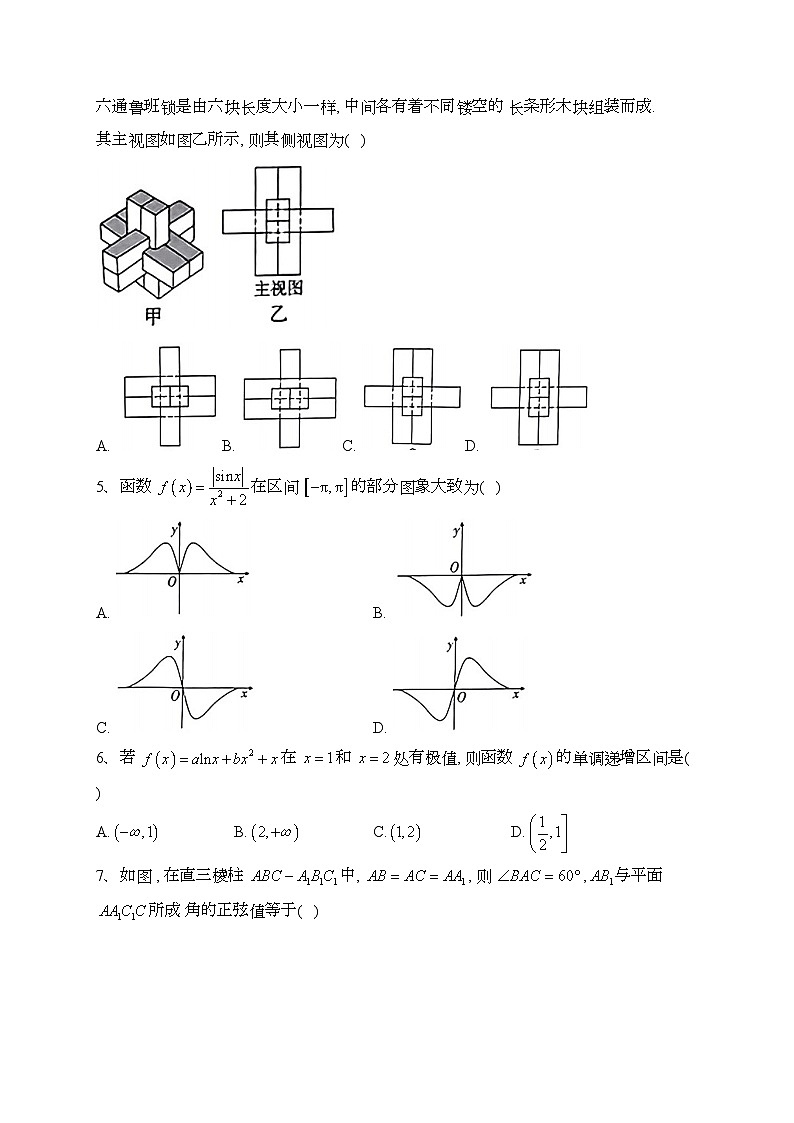
4、榫卯, 是一种中国传统建筑、家具及其他器械的主要结构方式, 是 在两个构件上采用凹凸部位相结合的一种连接方式. 春秋时期著名 的工匠碍班运用津卯结构制作出了砶班锁, 且鲁班锁可拆解, 但是 要将它们拼接起来则需要较啇的空间思维能力和足㿟的耐心. 如图 甲, 六通鲁班锁是由六块长度大小一样, 中间各有着不同镂空的 长条形木块组装而成. 其主视图如图乙所示, 则其侧视图为( )
A. B. C. D.
5、函数 在区间 的部分图象大致为( )
A. B.
C. D.
6、若 在 和 处有极值, 则函数 的单调递增区间是( )
A. B. C. D.
7、如图 , 在直三棱柱 中, , 则 ,与平面 所成 角的正弦值等于( )
A. B. C. D.
8、《九章算术》是我国古代内容极为丰富的数学名著, 其中《方田》章给出 计算弧田面积所用的经验公式为: 弧田面积 (弦×矢+矢2), 弧田 (如图 )由圆弧和其所对弦所围成, 公式中 “弦”指圆弧所对弦长, “矢” 等于 半径长与圆心到弦的距离之差. 现已知弧田面积为, 且弦是矢的 倍,按照上述经验公式计算所得弧田的弧长是( )
A. B. C. D.
9、已知椭圆, 直线 与椭圆交于A,B 两点, ,分别为椭圆的左、右 两个焦点, 直线 与椭圆交于另一个点D, 则直线AD 与BD 的斜率乘积为( )
A. B. C. D.
10、已知一圆锥内接于球, 圆雉的表面积是其底面面积的 3 倍, 则圆雉与球的体积之比是( )
A. B. C. D.
11、已知函数 若 在区间 内恰好有 4 个零点, 则a 的取值范围是( )
A. B. C. D.
12、已知正实数a,b,c 分别满足,,, 其中 e是自然常数, 则 a,b,c的大 小关系为( )
A. B. C. D.
二、填空题
13、已知平面向量,, 若, 则实数m 的值为______.
14、从-3,-1,1,3 这四个数中随机选取两个数分别记为k,b, 则直线 不经过第二象 限的概率为_______.
15、已知圆C 的圆心为双曲线 T的一个焦点F, 半径为双曲线T 的实半轴长. 若圆 C与双曲线T 的一条渐近线l 交于点M,N, 且, 则双曲线T 的离心率为________.
16、已知 的三边长分别为a,b,c, 若, 则 的取值范围是_______.
三、解答题
17、设数列 的前n 项和为, 当 时, 有.
(1)求证: 数列 是等差数列;
(2)若,, 求 的最大值.
18、如图所示, 在四棱锥 中, 底面ABCD 为直角梯形,,,,,,.
(1) 求证: 平面 平面ABCD;
(2) 求平面ADE 与平面BCE 所成二面角的余弦值.
19、为了 “让广大青少年充分认识到烁品的危害性, 切实提升青少年识毒防霉拒毒意识”, 我市 组织开展青少年禁拝知识竞赛,团员小明每天自觉登录 “禁毒知识竟赛 APP”, 参加各种学 习活动, 同时热衷于参与四人赛. 每局四人赛是由网络随机匹配四人进行比赛, 每题回答正 确得 20 分, 第 1 个达到 100 分的比赛者获得第 1 名, 赢得该局比赛, 该局比赛结束. 每天的 四人赛共有 20 局, 前 2 局是有效局, 根据得分情况获得相应名次, 从而得到相应的学习积 分, 第 1 局获得第 1 名的得 3 分, 获得第 2 、3 名的得 2 分, 获得第 4 名的得 1 分; 第 2 局获 得第 1 名的得 2 分, 获得第 2、3、4 名的得 1 分; 后 18 局是无效局, 无论获得什么名次, 均不能获得学习积分. 经统计, 小明每天在第 1 局四人赛中获得 3 分、2 分、1 分的概率分 别为,,, 在第 2 局四人赛中获得 2 分、 1 分的概率分别为,.
(1) 设小明每天获得的得分为X, 求X 的分布列和数学期望;
(2) 若小明每天赛完 20 局, 设小明在每局四人赛中获得第 1 名从而勍得该局比赛的概率为,每局是否赢得比赛相互独立、请问在每天的20局四人比赛中,小明赢得多少局的比赛概率最大?
20、实数,,.
(1)讨论 的单调性并写出过程;
(2)求证:.
21、椭圆 的左、右焦点分别为 ,,P是 C上的一个动点 (不在 x轴上), 射线 ,分别与C 交于点A,B, 记 ,的周长分别为,, 已 知.
(1)求椭圆C 的标准方程;
(2)记 ,,的面积分别为,,, 求证: 是定值.
22、在平面直角坐标系 xOy中, 曲线 的参数方程为 (为参数), 以坐标原点O 为 极点, x 轴正半轴为极轴建立极坐标系, 曲线 的极坐标方程为, 其 中.
(1)求曲线 与曲线 的交点的极坐标;
(2)直线 与曲线 , 分别交于 M,N两点 (异于极点O),P 为 上的动 点, 求 面积的最大值.
23、已知关于x 的不等式 对任意实数x 恒成立.
(1) 求实数m 的取值范围;
(2)记实数 m的最小值为M, 若a,b 均为正实数, 且, 求证:.
参考答案
1、答案:B
解析:,故,故选B.
2、答案:D
解析:,故故选D.
3、答案:C
解析:对于A:由题图知,2023年4月19日至4月25日的高速公路车流量的极差为,故A正确;对于B:易知2023年4月19日至4月25日的高速公路车流量的中位数为17,故B正确;对于C:2023年4月19日至4月21日的高速公路车流量波动更大,故C错误;对于D:2023年4月23日的高速公路车流量为22万车次,同比增长率为10%,设2022年4月23日的高速公路车流量为x万车次,则,解得,故D正确,故选C.
4、答案:A
解析:观察主视图中的木条位置和木条的层次位置,分析可知侧视图是A,故选A.
5、答案:A
解析:因为,所以,即函数为偶函数,排除C,D;因为,所以排除B,故选A.
6、答案:C
解析:,由已知得
解得
由,得
故选C.
7、答案: C
解析:如图,
取的中点D,连接,AD,在正三棱柱中,底面是正三角形,.又底面,.又,平面,为与平面所成角.由题意,
设,,,
在中,,
故选C.
8、答案:D
解析:如图,
由题意可得, 弧田面积(弦×矢+矢2)
,所以.
设圆半径为r,则有,即,
解得,故,在中,,所以,
所求弧长为,
故选D.
9、答案:B
解析:椭圆的方程为,直线过原点,
设,,,
又①,②,
①−②得,,
,
故选B.
10、答案:B
解析:如图所示,
设圆锥的底面圆圆心为点D,延长AD与球面交于B.
设圆锥底面半径为r,母线为l,则,得,
圆锥的高,设求半径为R,则中,,
有,即,
故,
故选B.
11、答案:C
解析:当时,对任意,在内最多有1个零点,不符题意;所以,当时,由可得或,则在上,有一个零点,所以在内有3个零点,即在内有3个零点,因为,所以,,所以,解得,
综上所述,a的取值范围为,
故选C.
12、答案:A
解析:由题意得,而,,,
则,,构造函数,,
可知当时,单调递增;当时,单调递减,
故,,由于在处取得最大值,故不等关系显然成立,故选A.
13、答案:
解析:由题意,向量与垂直,则,解得.
14、答案:
解析:设为“的所有组合”,则,设事件A为“直线不经过第二象限”,则要求,所以,从而.
15、答案:
解析:依题意可设圆与双曲线的一条渐近线交于点M,N,由可知为直角三角形,所以圆C与渐近线相交所得弦长,由题可得双曲线的一条渐近线为,所以焦点F到渐近线l的距离为,所以,得,所以双曲线C的离心率.
16、答案:
解析:依正弦定理,由知角A是钝角,则,当时,令,
,当且仅当时,取“=”,
即,当时,;
当时,令,,
令,,,所以在上单调递增,所以,即,综上得,所以的取值范围是.
17、答案:(1)见解析
(2) 60
解析:(1)证明:因为当时,有①,
所以当时,②,
由①−②,整理可得,
所以数列是等差数列.
(2)由(1)可知是等差数列,所以
可得
所以数列的公差,
所以,
所以.
又,所以当或时,Sn取到最大值为60.
18、答案: (1) 见解析
(2)
解析:(1)证明:为直角梯形,,.
又,,
平面
又平面,.
又,,
如图,作,,.
又,.
又,由勾股定理可知.
,平面ABCD.
平面ABE,平面平面ABCD.
(2)由(1)知平面BCE,,
平面BCE.
又,以为原点建立空间直角坐标系,
,,,
平面BCE,是平面BCE的一个法向量.
设为平面ADE的法向量,,,
令,.
设平面ADE与平面BCE所成的二面角为,且为锐角,
所以.
19、答案:(1)
(2) 小明赢得5局的比赛概率最大
解析:(1)记事件表示第一局获得i分,事件表示第二局获得i分,
这些事件相互独立,由条件知的可能值为5,4,3,2.
;
;
;
.
其分布列为
5 | 4 | 3 | 2 | |
.
(2)设小明每天赢得的局数为,则,
于是.
根据条件得
由①得,得,
同理由②得,所以,
又因为,所以,
因此在每天的20局四人赛中,小明赢得5局的比赛概率最大.
20、答案:(1)见解析
(2) 见解析
解析:(1)令,的定义域为.
.
①当时,时,,在上是增函数;
时,,在上是减函数;
时,,在上是增函数;
②当时,,
时,,在上是减函数;
时,在上是增函数;
③当时,,单调递增;
④当时,时,,在上是增函数,
时,,在上是减函数,
时,,是增函数.
(2)证明:由(1)得时,,在上是减函数,
即当时,,即,
即.令,,
求和即得.
21、答案:(1)
(2)见解析
解析:(1),
,
则,得,与联立解得,
所以椭圆C的标准方程为.
(2)证明:设, ,,则,
可设直线PA的方程为,其中,
联立得,
则,
同理可得,.
因为
,
所以
所以是定值.
22、答案:(1) 和
(2)
解析:(1)的参数方程为(为参数),消去可得,
,所以曲线的直角坐标方程为.
将,代入得,曲线的极坐标方程为
的极坐标方程为,联立可得,
所以曲线和曲线的交点极坐标为和.
(2)当时,,,.
显然当点P到直线MN的距离最大时,△PMN的面积最大,
直线MN的方程为,圆心到直线MN的距离为,
所以点P到直线MN的最大距离,
所以.
23、答案:(1)
(2)见解析
解析:(1)原不等式等价于,
解得
(2)证明:由(1)知
当且仅当时等号成立.
贵州省2023届高三上学期3+3+3高考备考诊断性联考(一)数学(理)试题(含答案): 这是一份贵州省2023届高三上学期3+3+3高考备考诊断性联考(一)数学(理)试题(含答案),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2023届贵州省3+3+3高三备考诊断性联考(一)文科数学试卷+答案: 这是一份2023届贵州省3+3+3高三备考诊断性联考(一)文科数学试卷+答案,共12页。
贵州省贵阳市2023届“3+3+3”高考备考诊断性联考卷(三)理数: 这是一份贵州省贵阳市2023届“3+3+3”高考备考诊断性联考卷(三)理数,共4页。












