江西省九江市2023届高三三模数学（文）试题（含答案）

这是一份江西省九江市2023届高三三模数学（文）试题（含答案），共8页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
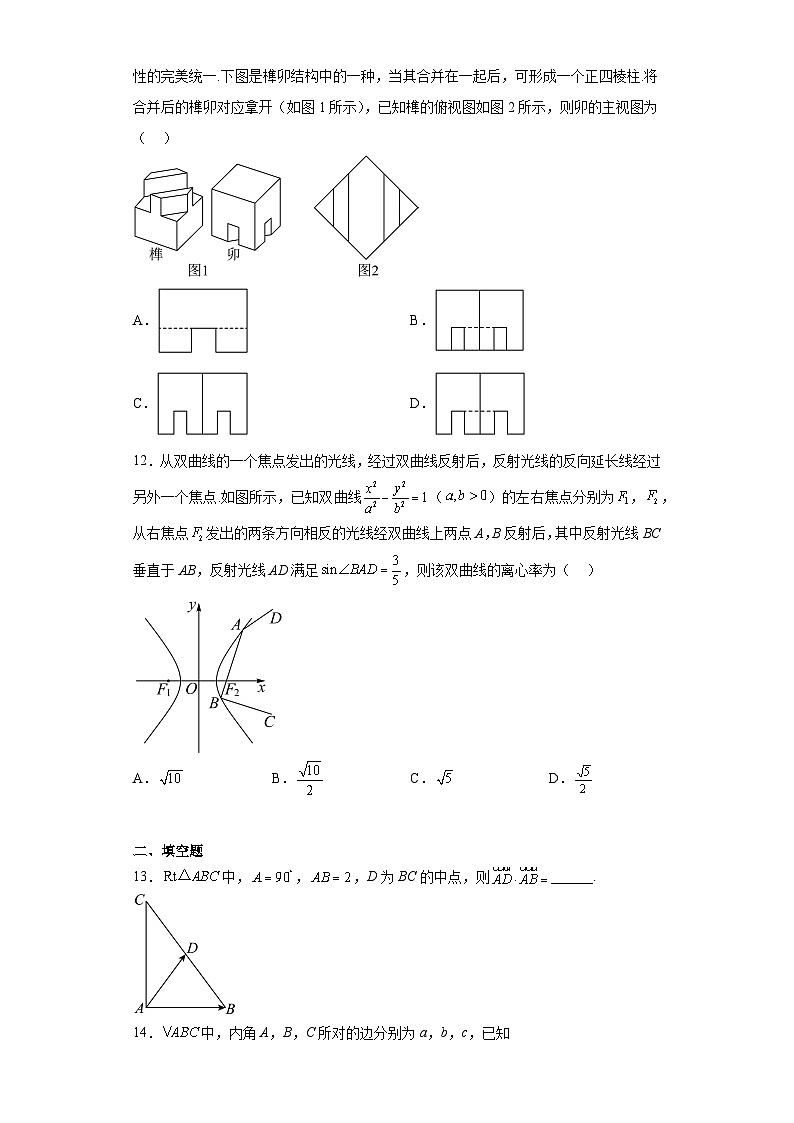
江西省九江市2023届高三三模数学（文）试题学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．已知集合，，则（    ）A． B． C． D．2．已知复数z满足，则（    ）A．1 B． C．2 D．3．已知，，，则（    ）A． B． C． D．4．为了强化节约意识，更好地开展“光盘行动”，某校组织社会实践小组对某块稻田的稻穗进行调研，小组随机抽取了20株稻穗，并统计了每株稻穗的粒数，整理得到如下茎叶图，则每穗粒数的中位数和平均数分别是（    ）A．174，175 B．175，175 C．175，174 D．174，1745．已知，且，，则（    ）A． B． C． D．6．执行如图所示的算法框图，则输出的C的值为（    ）A．0 B．1 C．2 D．37．若数列满足（q为常数，且），则称为差等比数列，其中q为公差比.已知差等比数列中，，，且公差比为2，则（    ）A．1024 B．1022 C．2048 D．20468．已知椭圆的左右焦点分别为，，，为平面内异于，的两点.若的中点在上，且，，则（    ）A．4 B． C．8 D．9．已知函数的部分图像如图所示.若，则的最大值为（    ）A．2 B． C．4 D．10．已知定义在R上的函数在上单调递增，是奇函数，的图像关于直线对称，则（    ）A．在上单调递减 B．在上单调递增C．在上单调递减 D．在上单调递增11．榫卯是一种中国传统建筑、家具的主要结构方式，它凝聚了中华文明的智慧.它利用材料本身特点自然连接，既符合力学原理，又重视实用和美观，达到了实用性和功能性的完美统一.下图是榫卯结构中的一种，当其合并在一起后，可形成一个正四棱柱.将合并后的榫卯对应拿开（如图1所示），已知榫的俯视图如图2所示，则卯的主视图为（    ）A． B．C． D．12．从双曲线的一个焦点发出的光线，经过双曲线反射后，反射光线的反向延长线经过另外一个焦点.如图所示，已知双曲线（）的左右焦点分别为，，从右焦点发出的两条方向相反的光线经双曲线上两点A，B反射后，其中反射光线BC垂直于AB，反射光线AD满足，则该双曲线的离心率为（    ）A． B． C． D． 二、填空题13．中，，，D为BC的中点，则______.14．中，内角A，B，C所对的边分别为a，b，c，已知，，则的面积为______.15．已知函数有两个极值点，，且，则______.16．如图，棱长为2的正方体中，P，Q为四边形内的点（包括边界），且点P到AB的距离等于到平面的距离，点Q到的距离等于到平面ABCD的距离，则的最小值为______. 三、解答题17．已知数列的前n项和为，且满足，.(1)求数列的通项公式；(2)求数列的前n项和.18．直三棱柱中，，D为的中点，.(1)求证：平面平面ABD；(2)若，求三棱锥的体积.19．2023年，国家不断加大对科技创新的支持力度，极大鼓舞了企业投入研发的信心，增强了企业的创新动能.某企业在国家一系列优惠政策的大力扶持下，通过技术革新和能力提升，极大提升了企业的影响力和市场知名度，订单数量节节攀升，右表为该企业今年1~4月份接到的订单数量.月份t1234订单数量y（万件）5.25.35.75.8附：相关系数，回归方程中斜率和截距的最小二乘法估计公式分别为，，.(1)试根据样本相关系数r的值判断订单数量y与月份t的线性相关性强弱（，则认为y与t的线性相关性较强，，则认为y与t的线性相关性较弱）.（结果保留两位小数）(2)建立y关于t的线性回归方程，并预测该企业5月份接到的订单数量.20．在平面直角坐标系xOy中，已知抛物线的焦点为F，A，B为E上两点，且点A的纵坐标为，F恰好是的重心.(1)求E的方程；(2)若，P，Q为抛物线上相异的两个动点，且，求的最小值.21．已知函数）在处的切线斜率为.(1)求a的值；(2)若，，求实数m的取值范围.22．在平面直角坐标系xOy中，已知曲线C的参数方程为（t为参数）.以O为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为，其中α为倾斜角，且.(1)求曲线C的普通方程和直线l的直角坐标方程；(2)设l与曲线C相交于P，Q两点，直线OP，OQ的斜率为，，求的取值范围.23．设a，b，c均为正数，已知函数的最小值为4.(1)求的最小值；(2)证明：.
参考答案：1．A2．B3．C4．A5．A6．C7．D8．D9．D10．C11．C12．B13．214．15．16．17．(1)(2) 18．(1)证明见解析(2) 19．(1)0.96，订单数量y与月份t的线性相关性较强(2)，6.05万件 20．(1)(2)11 21．(1)(2) 22．(1)，(2) 23．(1)(2)证明见解析