2023年九年级中考数学一轮复习 中点的妙用 课件

这是一份2023年九年级中考数学一轮复习 中点的妙用 课件，共19页。PPT课件主要包含了中考几何四大中点模型，把握考纲有的放矢，三线合一，小试身手，中位线定理，DEBC，倍长类中线等内容，欢迎下载使用。

1.通过探索与中点有关的几何问题培养学生观察和研究图形，联系中点相关知识进行联想，添加适当的辅助线，恰当地利用中点处理中点问题。2.通过专题形式的探索培养学生的逻辑思维能力。
学习目标
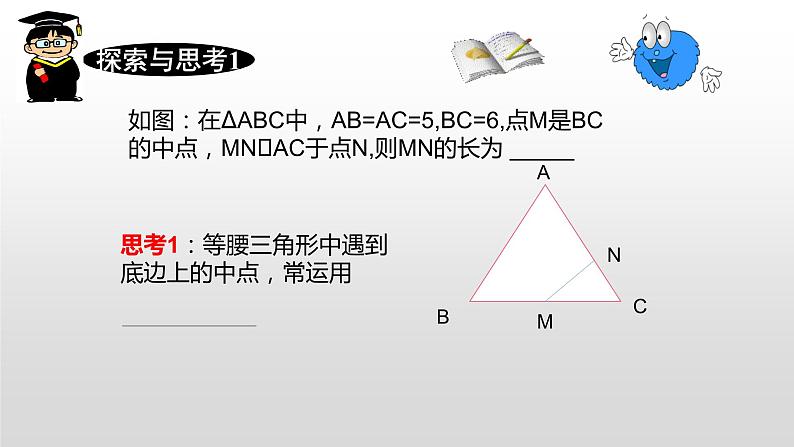
如图：在∆ABC中，AB=AC=5,BC=6,点M是BC的中点，MN⟂AC于点N,则MN的长为 _____
思考1：等腰三角形中遇到 底边上的中点，常运用
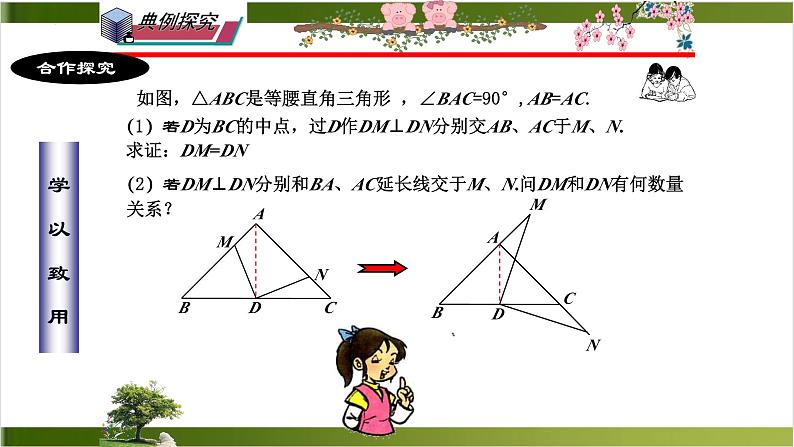
如图，△ABC是等腰直角三角形 ，∠BAC=90°,AB=AC.
（1）若D为BC的中点，过D作DM⊥DN分别交AB、AC于M、N. 求证：DM=DN
（2）若DM⊥DN分别和BA、AC延长线交于M、N.问DM和DN有何数量 关系？
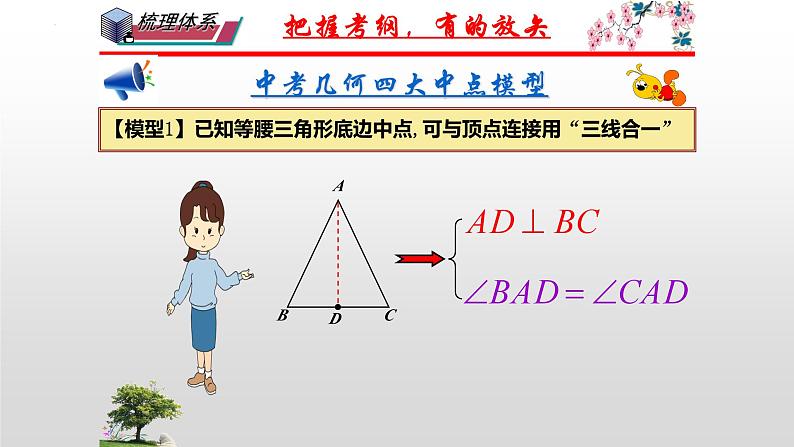
直角三角形斜边上的中线？
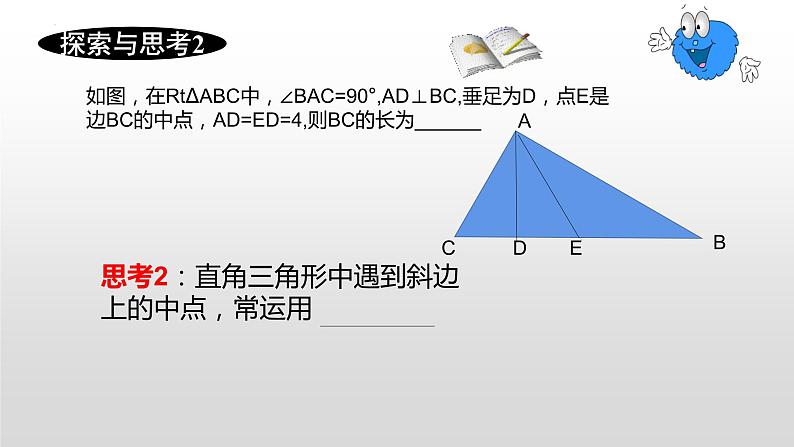
如图，在Rt∆ABC中，∠BAC=90°,AD⊥BC,垂足为D，点E是边BC的中点，AD=ED=4,则BC的长为______
思考2：直角三角形中遇到斜边上的中点，常运用
如图，四边形ABCD中，∠DAB=∠DCB=90°，点M、N分别是BD、AC的中点。MN、AC的位置关系如何？证明你的猜想。
如图，已知四边形ABCD的对角线AC与BD相交于点O，且AC=BD，M、N分别是AB、CD的中点，MN分别交BD、AC于点E、F.你能说出OE与OF的大小关系并加以证明吗？
思考3：三角形中遇到两边的中点，常运用
如图，在四边形ABCD中，M是对角线AC的中点，E、F分别是AD、BC的中点。
（1）请补充一个条件： ，使得∠MEF=∠MFE；
（2）根据题意结合你补充的条件，证明∠MEF=∠MFE.
如图，M是∆ABC的边BC的中点，AN平分∠BAC，BN⊥AN,且AB=10,BC=15,MN=3,则AC的长是
1.如图，在△ABC中，AD是三角形的中线，F为AD上一点，且BF=AC，连结并延长BF交AC于点E，求证：AE=EF.
小明遇到这样一个问题：如图1，在△ABC中，AB=7，AC=5，点D
为BC的中点，求AD的取值范围。
如图3，在正方形ABCD中，E为AB边的中点，G、F分别为AD、BC边上的点，若AG=2，BF=4，∠GEF=90°，求GF的长。
小明还发现：倍长中线法最重要的一点就是延长中线一倍，完成全等三角形的模型的构造。参考小明思考问题的方法，解决问题：