2022年浙江省丽水市青田县中考数学一模试卷

这是一份2022年浙江省丽水市青田县中考数学一模试卷，共28页。试卷主要包含了5≤x＜n+0，5－7，75这组数据错误．，5，，00，25等内容，欢迎下载使用。
2022年浙江省丽水市青田县中考数学一模试卷
一 、选择题（本大题有10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）
如果收入10元记作元，那么支出10元记作（ ）
A．元 B．元 C．元 D．元
如图是一些完全相同的小正方体搭成的几何体的三视图．这个几何体只能是（　　）

A． B． C． D．
若24×22＝2m，则m的值为（　　）
A．8 B．6 C．5 D．2
如图，直线m∥n，则∠α为（　　）

A．70° B． 65° C． 50° D． 40°
为了了解某班同学一周的课外阅读量，任选班上15名同学进行调查，统计如表，则下列说法错误的是（　　）
阅读量（单位：本/周）
0
1
2
3
4
人数（单位：人）
1
4
6
2
2
A．中位数是2 B．平均数是2 C．众数是2 D．极差是2
若关于x的分式方程＝+5的解为正数，则m的取值范围为（　　）
A．m＜﹣10 B．m≤﹣10
C．m≥﹣10且m≠﹣6 D．m＞﹣10且m≠﹣6
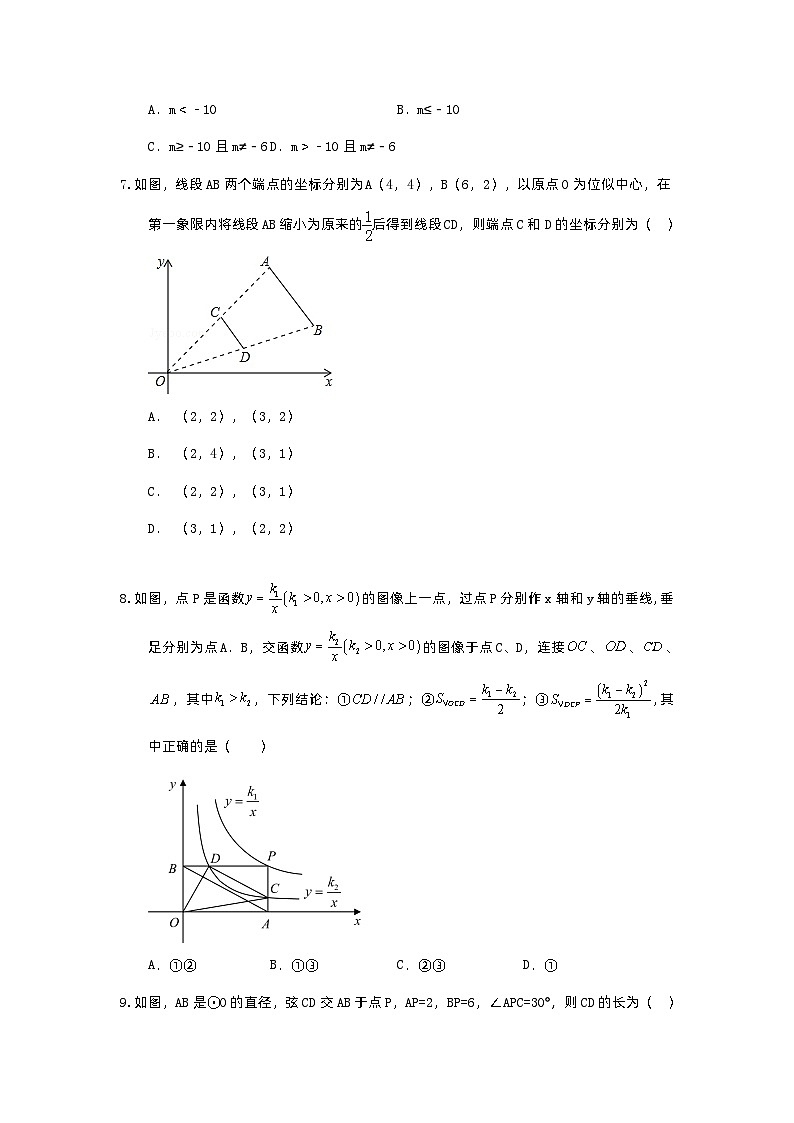
如图，线段AB两个端点的坐标分别为A（4，4），B（6，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，则端点C和D的坐标分别为（　　）

A． （2，2），（3，2）
B． （2，4），（3，1）
C． （2，2），（3，1）
D． （3，1），（2，2）

如图，点P是函数的图像上一点，过点P分别作x轴和y轴的垂线，垂足分别为点A．B，交函数的图像于点C、D，连接、、、，其中，下列结论：①；②；③，其中正确的是（ ）

A．①② B．①③ C．②③ D．①
如图，AB是⊙O的直径，弦CD交AB于点P，AP=2，BP=6，∠APC=30°，则CD的长为（　　）

A． B．2 C．2 D．8
正方形ABCD的对角线相交于点O（如图1），如果∠BOC绕点O按顺时针方向旋转，其两边分别与边AB、BC相交于点E、F（如图2），连接EF，那么在点E由B到A的过程中，线段EF的中点G经过的路线是（　　）

A．线段 B．圆弧 C．折线 D．波浪线
二 、填空题（本大题共6小题，每小题4分，共24分）
函数中，自变量的取值范围是_____．
﹣2的相反数的值等于　 　．
方程+＝1的解是　 　．
如图，在△ABC中，∠C＝90°，AC＝BC．以点A为圆心，以任意长为半径作弧交AB，AC于D，E两点，分别以点D，E为圆心，以大于DE长为半径作弧，在∠BAC内两弧相交于点P，作射线AP交BC于点F，过点F作FG⊥AB，垂足为G．若AB＝8cm，则△BFG的周长等于 　 　cm．

对非负实数x“四舍五入”到个位的值记为（x），即当n为非负整数时，若n﹣0.5≤x＜n+0.5，则（x）＝n．如（1.34）＝1，（4.86）＝5．若（0.5x﹣1）＝6，则实数x的取值范围是　 　．
如图，在中，对角线，BD交于点O,，于点，若AB=2，，则的长为__________________．

三 、解答题（本大题有7个小题，共66分．解答应写出文字说明、证明过程或演算步骤）
计算：（﹣）﹣2﹣（4﹣）0+6sin45°﹣．
我国新冠疫情防控取得了阶段性胜利．学生们返校学习后，某数学兴趣小组对本校同学周末参加体育运动的情况进行抽样调查，在校园内随机抽取男女生各人，调查情况如下表：
是否参加体育运动
男生
女生
总数
是



否



对男女生是否参加体育运动的人数绘制了条形统计图如图（1）．在这次调查中，对于参加体育运动的同学，同时对其参加的主要运动项目也进行了调查，并绘制了扇形统计图如图（2）．

根据以上信息解答下列问题：（1）______，______，_______；
（2）将图（1）所示的条形统计图补全；
（3）这次调查中，参加体育运动，且主要运动项目是球类的共有______人；
（4）在这次调查中，共有名男生未参加体育运动，分别是甲、乙、丙、丁四位同学，现在从他们中选出两位同学参加“我运动，我健康”的知识讲座，求恰好选出甲和乙去参加讲座的概率．（用列表或树状图解答）
如图，B、F、C、E是直线l上的四点，．

（1）求证：；
（2）将沿直线l翻折得到．
①用直尺和圆规在图中作出（保留作图痕迹，不要求写作法）；
②连接，则直线与l的位置关系是__________．
我国传统的计重工具﹣﹣秤的应用，方便了人们的生活．如图1，可以用秤砣到秤纽的水平距离，来得出秤钩上所挂物体的重量．称重时，若秤杆上秤砣到秤纽的水平距离为x（厘米）时，秤钩所挂物重为y（斤），则y是x的一次函数．下表中为若干次称重时所记录的一些数据．
x（厘米）
1
2
4
7
11
12
y（斤）
0.75
1.00
1.50
2.75
3.25
3.50
（1）在上表x，y的数据中，发现有一对数据记录错误．在图2中，通过描点的方法，观察判断哪一对是错误的？
（2）根据（1）的发现，问秤杆上秤砣到秤纽的水平距离为16厘米时，秤钩所挂物重是多少？

如图，航拍无人机从A处测得一幢建筑物顶部C的仰角是30°，测得底部B的俯角是60° ，此时无人机与该建筑物的水平距离AD是9米，那么该建筑物的高度BC为__________米（结果保留根号）．

如图，抛物线与轴交于、两点，且，对称轴为直线．
（1）求该抛物线的函数达式；
（2）直线过点且在第一象限与抛物线交于点．当时，求点的坐标；
（3）点在抛物线上与点关于对称轴对称，点是抛物线上一动点，令，当，时，求面积的最大值（可含表示）．

如图1，矩形DEFG中，DG＝2，DE＝3，Rt△ABC中，∠ACB＝90°，CA＝CB＝2，FG，BC的延长线相交于点O，且FG⊥BC，OG＝2，OC＝4．将△ABC绕点O逆时针旋转α（0°≤α＜180°）得到△A′B′C′．
（1）当α＝30°时，求点C′到直线OF的距离．
（2）在图1中，取A′B′的中点P，连结C′P，如图2．
①当C′P与矩形DEFG的一条边平行时，求点C′到直线DE的距离．
②当线段A′P与矩形DEFG的边有且只有一个交点时，求该交点到直线DG的距离的取值范围．






答案解析
一 、选择题
【考点】正负数在实际生活中的应用
【分析】根据正负数的含义，可得：收入记作“+”，则支出记作“-”，据此求解即可．
解：如果收入10元记作+10元，那么支出10元记作-10元．
故选：B．
【点评】此题主要考查了正负数在实际生活中的应用，要熟练掌握，解答此题的关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．
【考点】由三视图判断几何体．
【分析】根据三视图的定义一一判断即可．
解：观察图象可知，选项A符合题意．
故选：A．
【点评】考查学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查．如果掌握口诀“俯视图打地基，主视图疯狂盖，左视图拆违章”就更容易得到答案．
【考点】同底数幂的乘法．
【分析】同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加．
解：∵24×22＝24+2＝26＝2m，
∴m＝6，
故选：B．
【点评】本题考查了同底数幂的乘法，掌握幂的运算法则是解答本题的关键．
【考点】平行线的性质；邻补角的定义
【分析】利用平行线的性质和邻补角的定义解之
解∵m∥n，
∴∠α=∠1=∠1=180°﹣130°=50°
故选C．

【点评】本题考查平行线的性质、记住两直线平行同位角相等，两直线平行同旁内角互补，两直线平行内错角相等，属于中考常考题型．
【考点】极差；加权平均数；中位数；众数．
【分析】根据表格中的数据，求出中位数，平均数，众数，极差，即可做出判断．
解：15名同学一周的课外阅读量为0，1，1，1，1，2，2，2，2，2，2，3，3，4，4，
中位数为2；
平均数为（0×1+1×4+2×6+3×2+4×2）÷15=2；
众数为2；
极差为4﹣0=4；
所以A．B、C正确，D错误．
故选D．
【点评】此题考查了极差，平均数，中位数，众数，熟练掌握各自的求法是解本题的关键．
【考点】解分式方程
【分析】分式方程去分母化为整式方程，表示出方程的解，由分式方程的解为正数求出m的范围即可．
解：去分母得，
解得，
由方程的解为正数，得到，且，，
则m的范围为且，
故选：D．
【点评】本题主要考查了分式方程的计算，去分母化为整式方程，根据方程的解求出m的范围，其中考虑到分式方程的分母不可为零是做对题目的关键．
【考点】位似变换；坐标与图形性质．
【分析】直接利用位似图形的性质得出对应点坐标乘以得出即可．
解：∵线段AB两个端点的坐标分别为A（4，4），B（6，2），
以原点O为位似中心，在第一象限内将线段AB缩小为原来的后得到线段CD，
∴端点的坐标为：（2，2），（3，1）．
故选：C．
【点评】此题主要考查了位似变换，正确把握位似图形的性质是解题关键．
【考点】反比例函数系数k的几何意义，反比例函数图象上点的坐标特征
【分析】设P（m，），分别求出A，B，C，D的坐标，得到PD，PC，PB，PA的长，判断和的关系，可判断①；利用三角形面积公式计算，可得△PDC的面积，可判断③；再利用计算△OCD的面积，可判断②．
解：∵PB⊥y轴，PA⊥x轴，点P在上，点C，D在上，
设P（m，），
则C（m，），A（m，0），B（0，），令，
则，即D（，），
∴PC==，PD==，
∵，，即，
又∠DPC=∠BPA，
∴△PDC∽△PBA，
∴∠PDC=∠PBC，
∴CD∥AB，故①正确；
△PDC的面积===，故③正确；

=
=
=
=
=，故②错误；
故选B．
【点评】此题主要考查了反比例函数的图象和性质，k的几何意义，相似三角形的判定和性质，解题关键是表示出各点坐标，得到相应线段的长度．
【考点】垂径定理，勾股定理，含30度的直角三角形
【分析】作OH⊥CD于H，连结OC，如图，根据垂径定理由OH⊥CD得到HC=HD，再利用AP=2，BP=6可计算出半径OA=4，则OP=OA﹣AP=2，接着在Rt△OPH中根据含30度的直角三角形的性质计算出OH=OP=1，然后在Rt△OHC中利用勾股定理计算出CH=，所以CD=2CH=2．
解：作OH⊥CD于H，连结OC，如图，
∵OH⊥CD，
∴HC=HD，
∵AP=2，BP=6，
∴AB=8，
∴OA=4，
∴OP=OA﹣AP=2，
在Rt△OPH中，∵∠OPH=30°，
∴∠POH=60°，
∴OH=OP=1，
在Rt△OHC中，∵OC=4，OH=1，
∴CH==，
∴CD=2CH=2．
故选：C．

【点评】本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理以及含30度的直角三角形的性质．
【考点】轨迹,旋转的性质,全等三角形的判定与性质,正方形的性质．
【分析】建立如图平面直角坐标系，设正方形ABCD的边长为1，证明△AOE≌△BOF（ASA），推出AE＝BF，设AE＝BF＝a，则F（a，0），E（0，1﹣a），由题意G（a，﹣a），推出点G在直线y＝﹣x+上运动，可得结论．
解：建立如图平面直角坐标系，设正方形ABCD的边长为1，

∵四边形ABCD是正方形，
∴OAE＝∠OBF＝45°，OA＝OB，
∵∠AOB＝∠EOF＝90°，
∴∠AOE＝∠BOF，
∴△AOE≌△BOF（ASA），
∴AE＝BF，
设AE＝BF＝a，则F（a，0），E（0，1﹣a），
∵EG＝FG，
∴G（a，﹣a），
∴点G在直线y＝﹣x+上运动，
∴点G的运动轨迹是线段，
故选：A．
【点评】本题考查正方形的性质，全等三角形的判定和性质等知识，解题的关键是学会构建平面直角坐标系，利用一次函数解决轨迹问题，属于中考选择题中的压轴题．
二 、填空题
【考点】函数自变量的取值范围
【分析】根据被开方式是非负数列式求解即可.
解：依题意，得，
解得：，
故答案为．
【点评】本题考查了函数自变量的取值范围，函数有意义时字母的取值范围一般从几个方面考虑：①当函数解析式是整式时，字母可取全体实数；②当函数解析式是分式时，考虑分式的分母不能为0；③当函数解析式是二次根式时，被开方数为非负数．④对于实际问题中的函数关系式，自变量的取值除必须使表达式有意义外，还要保证实际问题有意义．
【考点】相反数
【分析】根据相反数的定义作答．
解：﹣2的相反数的值等于 2．
故答案是：2．
【点评】考查了相反数的概念：只有符号不同的两个数叫做互为相反数．
【考点】解分式方程，解一元二次方程
【分析】去分母，把分式方程化为整式方程，求解并验根即可．
解：
去分母，得（2x﹣1）（x+1）﹣2＝（x+1）（x﹣1）
去括号，得2x2+x﹣3＝x2﹣1
移项并整理，得x2+x﹣2＝0
所以（x+2）（x﹣1）＝0
解得x＝﹣2或x＝1
经检验，x＝﹣2是原方程的解．
故答案为：x＝﹣2．
【点评】本题考查了分式方程、一元二次方程的解法．掌握分式方程的解法是解决本题的关键．注意验根．
【考点】作图—基本作图，角平分线的性质，等腰直角三角形．
【分析】直接利用基本作图方法结合全等三角形的判定与性质进而得出AC＝AG，即可得出答案．
解：在△ABC中，
∵∠C＝90°，
∴FC⊥AC，
∵FG⊥AB，
由作图方法可得：AF平分∠BAC，
∴∠BAF＝∠CAF，FC＝FG，
在Rt△ACF和Rt△AGF中，
，
∴Rt△ABD≌Rt△AED（HL），
∴AC＝AG，
∵AC＝BC，
∴AG＝BC，
∴△BFG的周长＝GF+BF+BG＝CF+BF+BG＝BC+BG＝AG+BG＝AB＝8cm．
故答案为：8．
【点评】此题主要考查了作图﹣基本作图以及全等三角形的判定与性质，正确理解基本作图方法是解题关键．
【考点】一元一次不等式组的应用
【分析】根据题意得到：6﹣0.5≤0.5x﹣1＜6+0.5，据此求得x的取值范围．
解：依题意得：6﹣0.5≤0.5x﹣1＜6+0.5
解得13≤x＜15．
故答案是：13≤x＜15．
【点评】考查了一元一次不等式组的应用，解题的关键是得到关于x的不等式组6﹣0.5≤0.5x﹣1＜6+0.5．
【考点】相似三角形的判定和性质，勾股定理
【分析】根据勾股定理求得AC的长，结合平行四边形的性质求得AO的长，然后利用相似三角形的判定和性质求解．
解：∵，，AB=2
∴在Rt△ABC中，AC=
∴在中，AO=
在Rt△ABO中，BO=
∵，
∴
又∵
∴
∴，
解得：AH=
故答案为：．
【点评】本题考查相似三角形的判定和性质以及勾股定理解直角三角形，掌握相关性质定理正确推理计算是解题关键．
三 、解答题
【考点】实数的运算，零指数幂，负整数指数幂，特殊角的三角函数值
【分析】直接利用二次根式的性质以及零指数幂的性质、负指数幂的性质分别化简得出答案．
解：原式＝9﹣1+6×﹣3
＝9﹣1+3﹣3
＝8．
【点评】此题主要考查了实数运算，正确化简各数是解题关键．
【考点】条形统计图，扇形统计图，列表法或树状图法
【分析】(1)根据表格的信息算出总数,根据扇形的比例求出a即可．
(2)根据表格的数量补全条形统计图即可．
(3)用参加体育运动的人数与球类的百分比相乘即可．
(4)画出树状图,列式求概率即可．
解：(1)m=21+19=40,
n=4+6=10,
a=100－45－7.5－7.5=40．
故答案为:40,10,40．
(2)如图所示:

(3)40×45%=18(人)．
故答案为:18．
(4)

P(恰好选出甲和乙参加讲座)=．
【点评】本题考查条形统计图、扇形统计图,关键在于结合图形得出有用信息．
【考点】全等三角形的判定和性质，平行四边形的判定和性质
【分析】（1）根据“SAS”即可证明；
（2）①以点B为圆心，BA为半径画弧，以点C为圆心，CA 为半径画画弧，两个弧交于，连接B，C，即可；
②过点作M⊥l，过点D 作DN⊥l，则M∥DN，且M=DN，证明四边形MND是平行四边形，即可得到结论．
（1）证明：∵，
∴BC=EF，
∵，
∴∠ABC=∠DEF，
又∵，
∴；
（2）①如图所示，即为所求；

②∥l，理由如下：
∵，与关于直线l对称，
∴，
过点作M⊥l，过点D 作DN⊥l，则M∥DN，且M=DN，
∴四边形MND是平行四边形，
∴∥l，
故答案是：平行．

【点评】本题主要考查全等三角形的判定和性质，平行四边形的判定和性质，添加辅助线，构造平行四边形是解题的关键．
【考点】一次函数的应用
【分析】（1）利用描点法画出图形即可判断．
（2）设函数关系式为y＝kx+b，利用待定系数法解决问题即可.
解：（1）观察图象可知：x＝7，y＝2.75这组数据错误．

（2）设y＝kx+b，把x＝1，y＝0.75，x＝2，y＝1代入可得，
解得，
∴，
当x＝16时，y＝4.5，
答：秤杆上秤砣到秤纽的水平距离为16厘米时，秤钩所挂物重是4.5斤.
【点评】此题考查画一次函数的图象的方法，待定系数法求一次函数的解析式，一次函数的实际应用，正确计算是解此题的关键.
【考点】解直角三角形的应用
【分析】由题意可得∠CAD=30°，∠BAD=60°，然后分别解Rt△ADC 和Rt△ADB，求出CD和BD的长，进一步即可求得结果．
解：由题意，得∠CAD=30°，∠BAD=60°，
则在Rt△ADC中，米，
在Rt△ADB中，米，
∴BC=33+93=123米．
故答案为：123．
【点评】本题考查了解直角三角形的应用，属于常考题型，正确理解题意、熟练掌握解直角三角形的知识是解题关键．
【考点】二次函数综合题
【分析】（1）根据已知点和对称轴，用待定系数法求二次函数的解析式即可；
（2）由得等腰直角三角形，从而求得坐标；
（3分情况讨论，在对称轴的左右两边，即当，时分别求得面积的最大值
解：（1）∵抛物线过，对称轴为，
∴，
解得
∴抛物线表达式为．
（2）过点作轴于点，

∵，
∴，
设点的横坐标为，
则纵坐标为，
∴，
代入，得：
．
解得（舍去），，
∴
∴点的坐标是（6，7）．
（3）由（2）得的坐标是（6，7）
∵对称轴，
∴点的坐标是（－2，7），
∴，
∵与轴平行，点在轴下方，
设以为底边的高为
则，
∴当最大值时，的面积最大，
∵，，
①当时，，
此时在上随的增大而减小．
∴，
∴，
∴的最大面积为：
．
②当时，此时的对称轴
含于内
∴，
∴，
∴的最大面积为：
．
综上所述：当时，的最大面积为，
当时，的最大面积为64.
【点评】本题考查了用待定系数法求函数表达式，二次函数图像与性质，二次函数求最值问题，熟练掌握二次函数的图像与性质是解决本题的关键．
【考点】四边形综合题
【分析】（1）过点C′作C′H⊥OF于H．根据直角三角形的边角关系，解直角三角形求出CH即可．
（2）①分两种情形：当C′P∥OF时，过点C′作C′M⊥OF于M；当C′P∥DG时，过点C′作C′N⊥FG于N．通过解直角三角形，分别求出C′M，C′N即可．
②设d为所求的距离．第一种情形：当点A′落在DE上时，连接OA′，延长ED交OC于M．当点P落在DE上时，连接OP，过点P作PQ⊥C′B′于Q．结合图象可得结论．
第二种情形：当A′P与FG相交，不与EF相交时，当点A′在FG上时，A′G＝2﹣2，即d＝2﹣2；当点P落在EF上时，设OF交A′B′于Q，过点P作PT⊥B′C′于T，过点P作PR∥OQ交OB′于R，连接OP．求出QG可得结论．
第三种情形：当A′P经过点F时，此时显然d＝3．综上所述即可得结论．
解：（1）如图，

过点C′作C′H⊥OF于H．
∵△A′B′C′是由△ABC绕点O逆时针旋转得到，
∴C′O=CO=4，
在Rt△HC′中，
∵∠HC′O＝α＝30°，
∴C′H＝C′O•cos30°＝2，
∴点C′到直线OF的距离为2．
（2）①如图，当C′P∥OF时，过点C′作C′M⊥OF于M．

∵△A′B′C′为等腰直角三角形，P为A′B′的中点，
∴∠A′C′P=45°，
∵∠A′C′O=90°，
∴∠OC′P=135°.
∵C′P∥OF，
∴∠O＝180°﹣∠OC′P＝45°，
∴△OC′M是等腰直角三角形，
∵OC′＝4，
∴C′M＝C′O•cos45°=4×=，
∴点C′到直线DE的距离为．
如图，当C′P∥DG时，过点C′作C′N⊥FG于N．

同法可证△OC′N是等腰直角三角形，
∴C′N＝，
∵GD=2，
∴点C′到直线DE的距离为．
②设d为所求的距离．
第一种情形：如图，当点A′落在DE上时，连接OA′，延长ED交OC于M．

∵OC=4，AC=2，∠ACO=90°，

∵OM＝2，∠OMA′＝90°，
∴A′M＝＝＝4，
又∵OG=2，
∴DM=2，
∴A′D＝A′M-DM=4-2=2，
即d＝2，
如图，当点P落在DE上时，连接OP，过点P作PQ⊥C′B′于Q．

∵P为A′B′的中点，∠A′C′B′=90°，
∴PQ∥A′C′，
∴
∵B′C′=2
∴PQ＝1，C'Q=1，
∴Q点为B′C′的中点，也是旋转前BC的中点，
∴OQ=OC'+C'Q=5
∴OP＝＝，
∴PM＝，
∴PD＝，
∴d＝﹣2，
∴2≤d≤﹣2．
第二种情形：当A′P与FG相交，不与EF相交时，当点A′在FG上时，A′G＝2﹣2，即d＝2﹣2，
如图，当点P落在EF上时，设OF交A′B′于Q，过点P作PT⊥B′C′于T，过点P作PR∥OQ交OB′于R，连接OP．

由上可知OP＝，OF＝5，
∴FP＝＝＝1，
∵OF＝OT，PF＝PT，∠F＝∠PTO＝90°，
∴Rt△OPF≌Rt△OPT（HL），
∴∠FOP＝∠TOP，
∵PR∥OQ，
∴∠OPR＝∠POF，
∴∠OPR＝∠POR，
∴OR＝PR，
∵PT2+TR2＝PR2，

∴PR＝2.6，RT＝2.4，
∵△B′PR∽△B′QO，
∴＝，
∴＝，
∴OQ＝，
∴QG＝OQ﹣OG＝，即d＝
∴2﹣2≤d＜，
第三种情形：当A′P经过点F时，如图，
此时FG=3，即d＝3．

综上所述，2≤d＜或d＝3．