专题16 图形的初步认识-2023年中考数学一轮复习热点题型与方法精准突破（原卷版）

专题16 图形的初步认识

【考查题型】

【知识要点】

知识点一 几何图形

几何图形的概念: 我们把实物中抽象出来的各种图形叫做几何图形,几何图形分为平面图形和立体图形。

立体图形的概念：图形所表示的各个部分不在同一平面内的图形，如圆柱体。

【常见的立体图形的种类】棱柱、棱锥、圆柱、圆锥、球等。

平面图形的概念：图形所表示的各个部分在同一平面内的图形，如三角形、正方形。

【常见的平面图形的种类】线段、角、三角形、长方形、圆等。

立体图形和平面的区别:

1）所含平面数量不同：

①平面图形是各个部分存在于一个平面上的图形；

②立体图形是由一个或者多个平面形成的图形，各部分不在同一平面内，且不同的立体图形所含的平面数量不一定相同。

2、性质不同。

①根据“点动成线，线动成面，面动成体”的原理可知，平面图形是由不同的点组成的；

②而立体图形是由不同的平面图形构成的，由构成原理可知平面图形是构成立体图形的基础。

3、观察角度不同。

①平面图形只能从一个角度观察；

②立体图形可从不同的角度观察，如左视图，正视图、俯视图等，且观察结果不同。

4、具有属性不同。

①平面图形只有长宽属性，没有高度；

①而立体图形具有长宽高的属性。

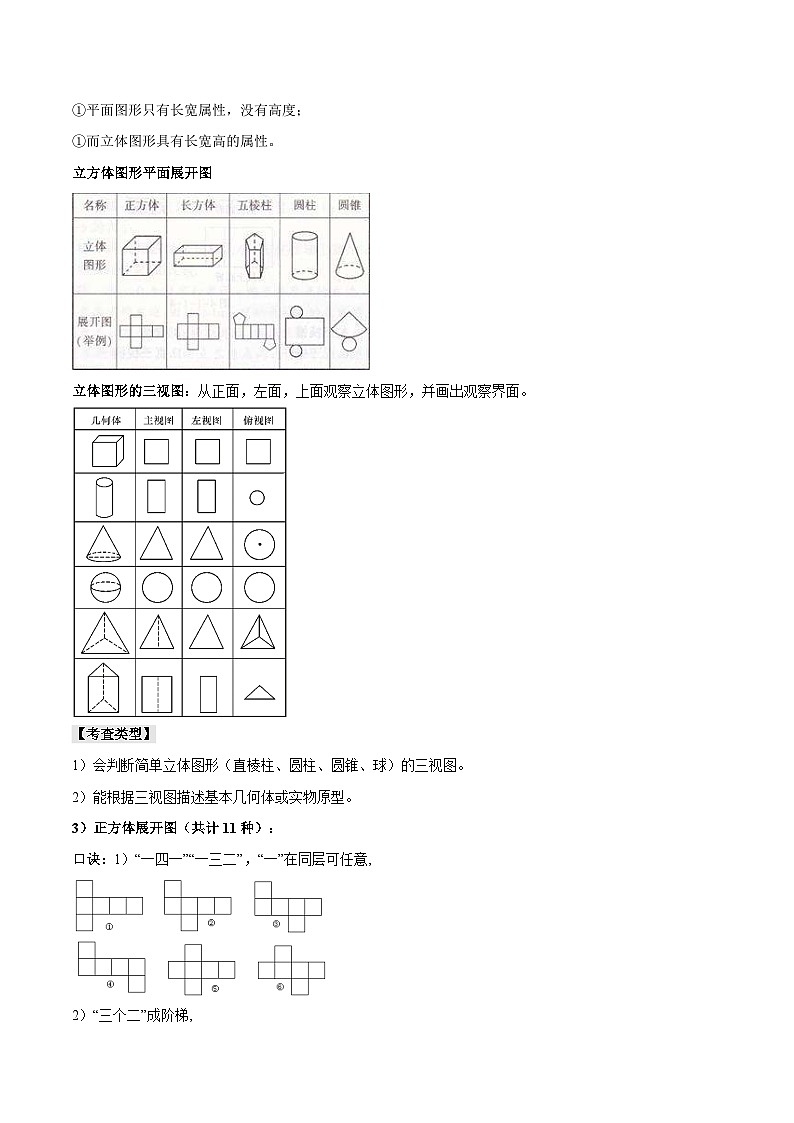
立方体图形平面展开图

立体图形的三视图：从正面，左面，上面观察立体图形，并画出观察界面。

【考查类型】

1）会判断简单立体图形（直棱柱、圆柱、圆锥、球）的三视图。

2）能根据三视图描述基本几何体或实物原型。

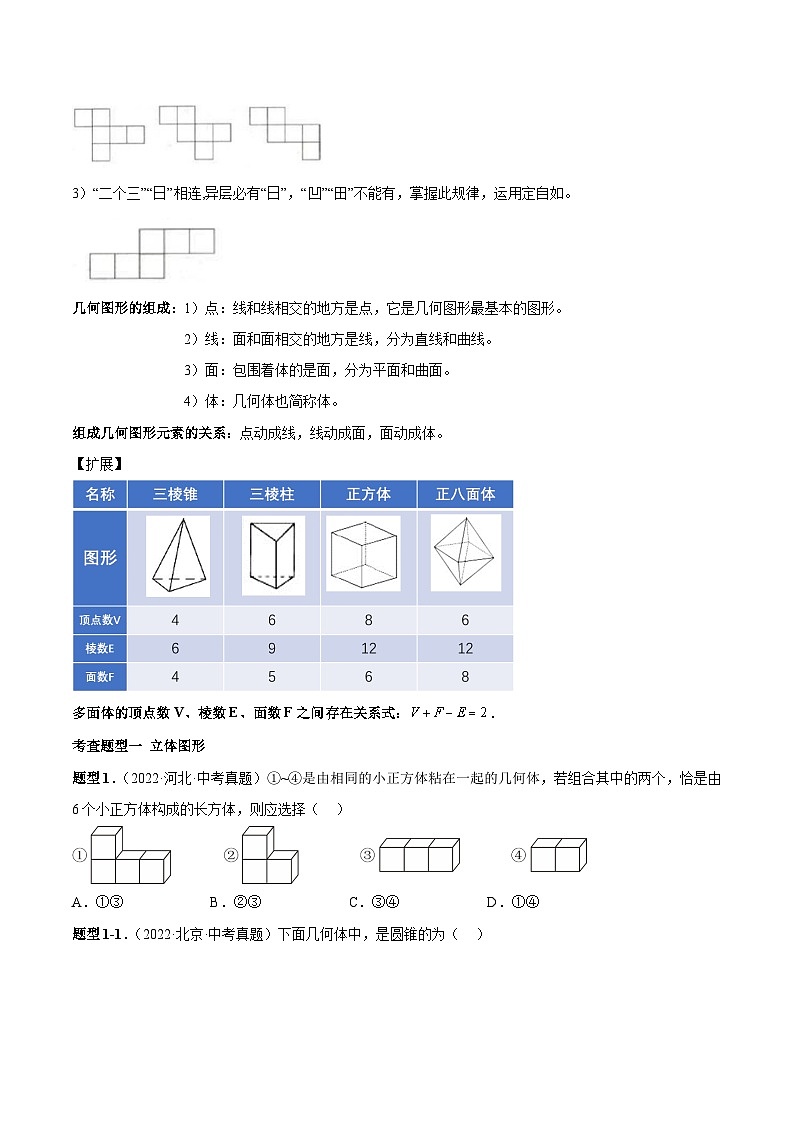
3）正方体展开图（共计11种）：

口诀：1）“一四一”“一三二”，“一”在同层可任意,

2）“三个二”成阶梯,

3）“二个三”“日”相连,异层必有“日”，“凹”“田”不能有，掌握此规律，运用定自如。

几何图形的组成：1）点：线和线相交的地方是点，它是几何图形最基本的图形。

2）线：面和面相交的地方是线，分为直线和曲线。

3）面：包围着体的是面，分为平面和曲面。

4）体：几何体也简称体。

组成几何图形元素的关系：点动成线，线动成面，面动成体。

【扩展】

多面体的顶点数V、棱数E、面数F之间存在关系式：．

考查题型一 立体图形

题型1．（2022·河北·中考真题）①~④是由相同的小正方体粘在一起的几何体，若组合其中的两个，恰是由6个小正方体构成的长方体，则应选择（    ）

A．①③ B．②③ C．③④ D．①④

题型1-1．（2022·北京·中考真题）下面几何体中，是圆锥的为（    ）

A． B． C． D．

题型1-2．（2022·山东威海·中考真题）如图所示的几何体是由五个大小相同的小正方体搭成的．其俯视图是(   )

A．B．C． D．

题型1-3．（2021·贵州安顺·中考真题）下列几何体中，圆柱体是（    ）

A． B． C． D．

考查题型二 几何体展开图的认识

题型2．（2022·四川广元·中考真题）如图是某几何体的展开图，该几何体是（    ）

A．长方体 B．圆柱 C．圆锥 D．三棱柱

题型2-1．（2022·广东广州·中考真题）如图是一个几何体的侧面展开图，这个几何体可以是（    ）

A．圆锥 B．圆柱 C．棱锥 D．棱柱

题型2-2．（2022·江苏常州·中考真题）下列图形中，为圆柱的侧面展开图的是（    ）

A．B．C． D．

题型2-3．（2022·江苏泰州·中考真题）如图为一个几何体的表面展开图，则该几何体是(   )

A．三棱锥 B．四棱锥 C．四棱柱 D．圆锥

题型2-4．（2021·浙江·中考真题）将如图所示的长方体牛奶包装盒沿某些棱剪开，且使六个面连在一起，然后铺平，则得到的图形可能是（    ）

A．B．C．D

考查题型三 正方体展开图的识别

题型3．（2022·江苏宿迁·中考真题）下列展开图中，是正方体展开图的是（    ）

A．B．C． D．

题型3-1．（2022·黑龙江绥化·中考真题）下列图形中，正方体展开图错误的是（    ）

A． B． C． D．

题型3-2．（2021·广东·中考真题）下列图形是正方体展开图的个数为（    ）

A．1个 B．2个 C．3个 D．4个

题型3-3．（2022·贵州六盘水·中考真题）如图，裁掉一个正方形后能折叠成正方体，但不能裁掉的是（    ）

A．① B．② C．③ D．④

考查题型四 正方体展开图上相对两个面上字/图案

题型4．（2022·河南·中考真题）2022年北京冬奥会的奖牌“同心”表达了“天地合·人心同”的中华文化内涵，将这六个汉字分别写在某正方体的表面上，如图是它的一种展开图，则在原正方体中，与“地”字所在面相对的面上的汉字是（    ）

A．合 B．同 C．心 D．人

题型4-1．（2022·江苏徐州·中考真题）如图，已知骰子相对两面的点数之和为7，下列图形为该骰子表面展开图的是（    ）

A．B．C．D．

题型4-2．（2022·山东淄博·中考真题）经过折叠可以围成正方体，且在正方体侧面上的字恰好环绕组成一个四字成语的图形是（    ）

A．B．C．D．

题型4-3．（2021·河北·中考真题）一个骰子相对两面的点数之和为7，它的展开图如图，下列判断正确的是（    ）

A．代表 B．代表

C．代表 D．代表

题型4-4．（2022·湖南常德·中考真题）如图是一个正方体的展开图，将它拼成正方体后，“神”字对面的字是________．

考查题型五 用七巧板拼图案

题型5．（2022·四川·巴中市教育科学研究所中考真题）七巧板是我国的一种传统智力玩具，下列用七巧板拼成的图形是轴对称图形的是（    ）

A． B． C． D．

题型5-1．（2021·山东枣庄·中考真题）小明有一个呈等腰三角形的积木盒，现在积木盒中只剩下如图的九个空格，下面有四种积木的搭配，其中不能放入的有（    ）

A．搭配① B．搭配② C．搭配③ D．搭配④

题型5-2．（2022·江西·中考真题）沐沐用七巧板拼了一个对角线长为2的正方形，再用这副七巧板拼成一个长方形（如图所示），则长方形的对角线长为__________．

知识点二 直线、射线、线段

【射线的表示方法】表示射线时端点一定在左边，而且不能度量，射线BA和射线AB是不同的射线。

经过若干点画直线数量：1）经过两点有一条直线，并且只有一条直线（直线公理）。

2）过三个已知点不一定能画出直线。

①当三个已知点在一条直线上时，可以画出一条直线；

②当三个已知点不在一条直线上时，不能画出直线。

线段的大小比较方法：1)度量法:分别用刻度尺测量线段AB、线段CD的长度，再进行比较

2)叠加法:让线段某一段端点重合，比较另一边两端点的位置。

线段中点的概念：把一条线段分成两条相等的线段的点叫线段中点。

距离的概念：连接两点间的线段的长度，叫做这两点的距离。两点的所有连线中，线段最短。简称：两点之间，线段最短。

考查题型六 两点确定一条直线

题型6．（2022·湖北十堰·中考真题）如图，工人砌墙时，先在两个墙脚的位置分别插一根木桩，再拉一条直的参照线，就能使砌的砖在一条直线上．这样做应用的数学知识是（    ）

A．两点之间，线段最短 B．两点确定一条直线

C．垂线段最短 D．三角形两边之和大于第三边

题型6-1．（2021·河北·中考真题）如图，已知四条线段，，，中的一条与挡板另一侧的线段在同一直线上，请借助直尺判断该线段是（    ）

A． B．

C． D．

题型6-2．（2021·浙江·中考真题）由沈康身教授所著，数学家吴文俊作序的《数学的魅力》一书中记载了这样一个故事：如图，三姐妹为了平分一块边长为1的祖传正方形地毯，先将地毯分割成七块，再拼成三个小正方形（阴影部分）．则图中的长应是______．

题型6-3．（2021·山东临沂·中考真题）数学知识在生产和生活中被广泛应用，下列实例所应用的最主要的几何知识，说法正确的是___（只填写序号）．

①射击时，瞄准具的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”；

②车轮做成圆形，应用了“圆是中心对称图形”；

③学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”；

④地板砖可以做成矩形，应用了“矩形对边相等”．

考查题型七 线段的和与差

题型7．（2022·山东临沂·中考真题）如图，，位于数轴上原点两侧，且．若点表示的数是6，则点表示的数是（   ）

A．-2 B．-3 C．-4 D．-5

题型7-1．（2021·江苏泰州·中考真题）互不重合的A、B、C三点在同一直线上，已知AC＝2a+1，BC＝a+4，AB＝3a，这三点的位置关系是（　　）

A．点A在B、C两点之间 B．点B在A、C两点之间

C．点C在A、B两点之间 D．无法确定

题型7-2．（2021·内蒙古·中考真题）已知线段，在直线AB上作线段BC，使得．若D是线段AC的中点，则线段AD的长为（   ）

A．1 B．3 C．1或3 D．2或3

题型7-3．（2022·浙江嘉兴·中考真题）如图，在ABC中，∠ABC＝90°，∠A＝60°，直尺的一边与BC重合，另一边分别交AB，AC于点D，E．点B，C，D，E处的读数分别为15，12，0，1，则直尺宽BD的长为_________．

考查题型八 两点之间线段最短

题型8．（2022·浙江金华·中考真题）如图，圆柱的底面直径为，高为，一只蚂蚁在C处，沿圆柱的侧面爬到B处，现将圆柱侧面沿“剪开”，在侧面展开图上画出蚂蚁爬行的最近路线，正确的是（    ）

A．B．C． D

题型8-1．（2022·广西柳州·中考真题）如图，从学校A到书店B有①、②、③、④四条路线，其中最短的路线是（　　）

A．① B．② C．③ D．④

题型8-2．（2021·江苏南京·中考真题）下列长度的三条线段与长度为5的线段能组成四边形的是（    ）

A．1，1，1 B．1，1，8 C．1，2，2 D．2，2，2

题型8-3．（2021·浙江台州·中考真题）小光准备从A地去往B地，打开导航、显示两地距离为37.7km，但导航提供的三条可选路线长却分别为45km，50km，51km（如图）．能解释这一现象的数学知识是（   ）

A．两点之间，线段最短 B．垂线段最短

C．三角形两边之和大于第三边 D．两点确定一条直线

知识点三 角

角的概念：由公共端点的两条射线所组成的图形叫做角（静态），角也可以看做由一条射线绕着它的端点旋转一定角度而形成的图（动态）。

角的分类：

角的表示法（四种）：

1)角可以用三个大写字母表示,但表示顶点的字母一定要写在中间。

2)用一个字母表示角, 必须是以这个字母为顶点的角，而且只有一个。

3)用一个数字表示角,在靠近顶点处画上弧线,写上数字。

4)用一个希腊字母表示,在靠近顶点处画上弧线,写上希腊字母。

角的度量：1°=60′；1′=60″；1直角=90°；1平角=180 °；1周角=360°　

角的大小的比较：1）叠合法：使两个角的顶点及一边重合，比较另一边的位置；

2）度量法：分别用量角器测量两个角的大小，再进行比较。

角的平分线：从一个角的顶点出发，把这个角分成相等的两个角的射线，叫做这个角的平分线。

余角概念：如果两个角的和等于直角，就说这两个角互为余角，即其中一个是另一个的余角。

补角概念：如果两个角的和等于平角，就说这两个角互为补角，即其中一个是另一个的补角。

【性质】等角的余角相等，等角的补角相等。

时针和分针所成的角度：钟表一周为360°，每一个大格为30°，每一个小格为6°.（每小时，时针转过30°，即一个大格，分针转过360°，即一周；每分钟，分针转过6°即一个小格）

考查题型九 与方向角有关的计算题

题型9．（2022·山东烟台·中考真题）如图，某海域中有A，B，C三个小岛，其中A在B的南偏西40°方向，C在B的南偏东35°方向，且B，C到A的距离相等，则小岛C相对于小岛A的方向是（　　）

A．北偏东70° B．北偏东75° C．南偏西70° D．南偏西20°

题型9-1．（2022·四川·巴中市教育科学研究所中考真题）一艘轮船位于灯塔的南偏东方向，距离灯塔30海里的处，它沿北偏东方向航行一段时间后，到达位于灯塔的北偏东方向上的处，此时与灯塔的距离约为________海里．（参考数据：，，）

题型9-2．（2022·湖南益阳·中考真题）如图，PA，PB表示以P为起点的两条公路，其中公路PA的走向是南偏西34，公路PB的走向是南偏东56，则这两条公路的夹角∠APB＝_____°．

题型9-3．（2022·湖北宜昌·中考真题）如图，岛在A岛的北偏东方向，岛在岛的北偏西方向，则的大小是_____．

题型9-4．（2021·广西玉林·中考真题）如图，某港口位于东西方向的海岸线上，甲、乙轮船同时离开港口，各自沿一固定方向航行，甲、乙轮船每小时分别航行12海里和16海里，1小时后两船分别位于点，处，且相距20海里，如果知道甲船沿北偏西方向航行，则乙船沿_____方向航行．

考查题型十 与余角和补角有关的计算

题型10．（2022·甘肃武威·中考真题）若，则的余角的大小是（　　）

A．50° B．60° C．140° D．160°

题型10-1．（2022·安徽·中考真题）两个矩形的位置如图所示，若，则（    ）

A． B． C． D．

题型10-2（2022·广西·中考真题）如图摆放一副三角板，直角顶点重合，直角边所在直线分别重合，那么∠BAC的大小为______

题型10-3．（2022·江苏连云港·中考真题）已知∠A的补角是60°，则_________．

题型10-4．（2022·广西玉林·中考真题）已知∠α=60°，则∠α的余角等于____度．