2023年+安徽省+黄山市九校联盟中考数学模拟试卷(含答案)

这是一份2023年+安徽省+黄山市九校联盟中考数学模拟试卷(含答案)，共21页。试卷主要包含了单选题，填空题等内容，欢迎下载使用。
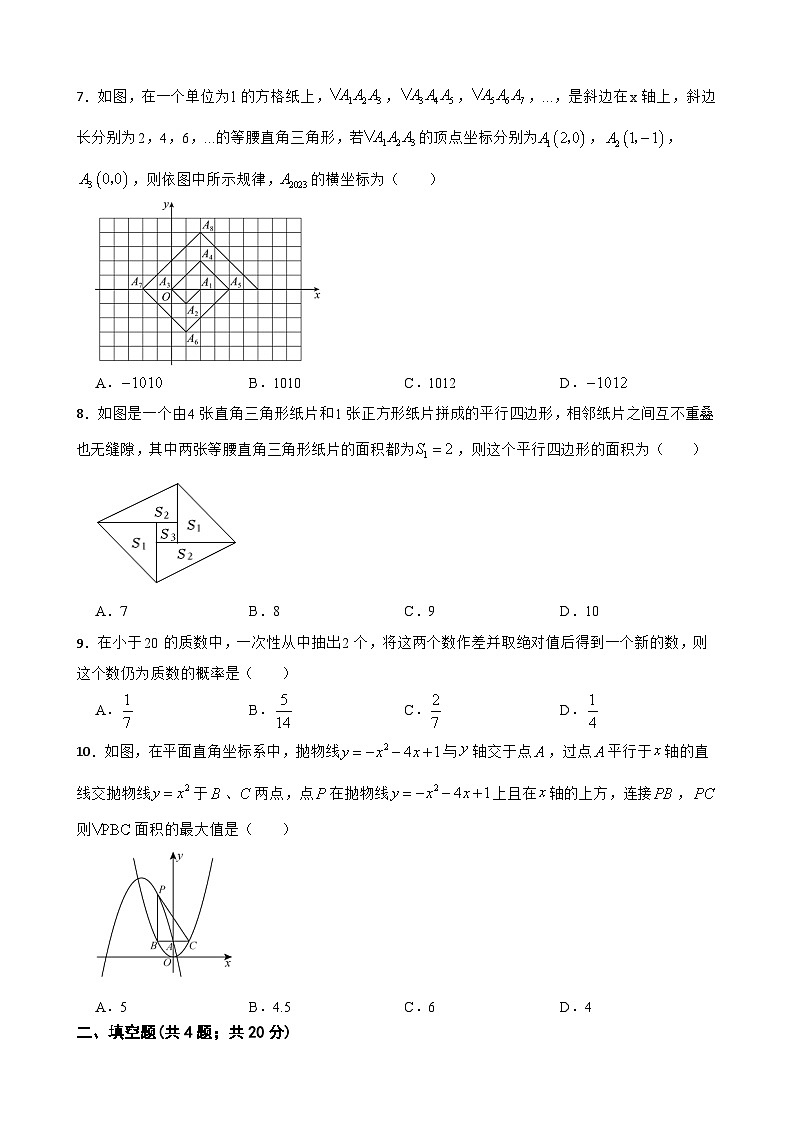
 2023年中考黄山市九校联盟数学模拟试卷一、单选题(共10题；共40分)1．6的倒数是（　　）A． B．-0.6 C． D．62．在我国《“十四五”就业促进规划》中明确提出，到2025年，城镇新增就业5500万人以上，数据5500万用科学记数法表示为（　　）A． B． C． D．3．下列运算正确的是（　　）A． B．C． D．4．下列几何体中，主视图与俯视图的形状不一样的几何体是（　　）A．       B．      C．      D．5．将一把直尺和一块含角的直角三角板按如图所示方式摆放，其中，，若，则的度数为（　　）A．12 B． C． D．6．如图，是某工程队修路的长度y（单位：m）与修路时间t（单位：天）之间的函数关系．该工程队承担了一项修路任务，任务进行一段时间后，工程队提高了工作效率，则该工程队提高效率前每天修路的长度是（　　） 米．A．150 B．110 C．75 D．707．如图，在一个单位为l的方格纸上，，，，...，是斜边在x轴上，斜边长分别为2，4，6，...的等腰直角三角形，若的顶点坐标分别为，，，则依图中所示规律，的横坐标为（　　）A． B．1010 C．1012 D．8．如图是一个由4张直角三角形纸片和1张正方形纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为，则这个平行四边形的面积为（　　）A．7 B．8 C．9 D．109．在小于20的质数中，一次性从中抽出2个，将这两个数作差并取绝对值后得到一个新的数，则这个数仍为质数的概率是（　　）A． B． C． D．10．如图，在平面直角坐标系中，抛物线与轴交于点，过点平行于轴的直线交抛物线于、两点，点在抛物线上且在轴的上方，连接，则面积的最大值是（　　）A．5 B．4.5 C．6 D．4二、填空题(共4题；共20分)11．不等式的解集为　     　．12．函数y＝中自变量的取值范围是　        　. 13．如图，是的直径，点D在的延长线上，切于点C，若，则的度数为　     　.14．如图，正方形的边长为4，E，F分别是边上的动点，且，连接交于点G，P是边上的另一个动点，连接，则的最小值为　     　.三、(共2题；共16分)15（8分）．计算：16（8分）．如图，在由边长为1个单位长度的小正方形组成的网格中，的顶点均为格点（网格线的交点）．（ 1 ）以A为旋转中心，将逆时针旋转，得到，请画出（ 2 ）将向上平移7个单位长度，再向左平移2个单位长度，得到，请画出四、(共2题；共16分)17（8分）．如图，海中小岛周围内有暗礁．渔船跟踪鱼群由西向东航行，在点处测得小岛在北偏东方向上；航行到达点，这时测得小岛在北偏东方向上．如果渔船不改变航线继续向东航行，有没有触礁的危险？（参考数据：，）18（8分）．观察下列三行数并按规律填空：－1，2，－3，4，－5，     ，     ，…；1，4，9，16，25，     ，     ，…；0，3，8，15，24，     ，     ，….（ 1 ）第一行数按什么规律排列？（ 2 ）第二行数、第三行数分别与第一行数有什么关系？（ 3 ）取每行数的第10个数，计算这三个数的和．五、(共2题；共20分)19（10分）．如图，已知A的坐标是，轴于点B，反比例函数的图象分别交AO，AB于点C，D，连接OD，的面积为2（1）求k的值和点C的坐标.（2）若点在该反比例函数图象上，且在的内部包括边界，求b的取值范围.20（10分）．已知：如图，为的直径，与相切于点C，交延长线于点D，连接，，，平分交于点E，过点B作，垂足为F.（1）求证：；（2）若，求线段的长.六、(共2题；共24分)21（12分）．为了丰富同学们的课余生活，某学校举行“亲近大自然”户外活动，现在随机抽取了部分学生进行主题为“你最想去的景点是？”的问卷调查，要求学生只能从“A（植物园），B（花卉园），C（湿地公园），D（森林公园）”四个景点中选择一项，根据调查结果绘制了如下两幅不完整的统计图．请根据图中信息回答下列问题：（1）本次调查的样本容量是　     　；（2）补全条形统计图：（3）若该学校共有3600名学生，试估计该校最想去森林公园的学生人数；（4）从选项为“D（森林公园）”的学生中抽取了小明和小军两人做游戏，游戏规则如下：每人从1，2，…，8中任意选择一个数字，然后两人各转动一次如图所示的转盘（转盘被分为面积相等的四个扇形），两人转出的数字之和等于谁选择的数，谁就获胜；若小军选择的数是5，用列表或画树状图的方法求他获胜的概率．22（12分）．海安宾馆有50个房间供游客居住．当每个房间的定价为180元时，房间会全部住满；当每个房间的定价每增加10元时，就会有一个房间空着．设房价为x元．（1）求宾馆每天的营业额y与房价x的函数关系式；（2）若有游客居住时，宾馆需要对每个房间支出20元的各种费用．房价定为多少时，宾馆利润W最大？（利润＝营业额－支出）六、(共1题；共14分)23．将正方形的边绕点A逆时针旋转至，记旋转角为，连接，过点B作直线，垂足为点F，连接．（1）如图1，当时，的形状为　               　，的值为　     　；（2）当时，①（1）中的两个结论是否仍然成立？如果成立，请根据图2的情形进行证明；如果不成立，请说明理由；②如图3，正方形边长为4，，，在旋转的过程中，是否存在与相似？若存在，则的值为            ，若不存在，请说明理由．
答案解析部分1．【答案】C【解析】【解答】解：6的倒数是，故答案为：C．
【分析】利用倒数的定义求解即可。2．【答案】A【解析】【解答】解：5500万， 故答案为：A． 【分析】 把一个大于10的数表示成a×10n的形式(其中a是整数数位只有一位的数，n是正整数)，这种计数法叫做科学记数法 。根据科学记数法的定义计算求解即可。3．【答案】A【解析】【解答】解：∵，故A符合题意；∵，故B不符合题意；∵，故C不符合题意；∵，故D不符合题意，故答案为：A.
【分析】根据积的乘方与幂的乘方、合并同类项、完全平方公式、同底数幂的乘法分别计算，再判断即可.4．【答案】C【解析】【解答】解：A. 正方体的主视图与俯视图都是正方形，故该选项不符合题意；B.圆柱的主视图与俯视图都是长方形，故该选项不符合题意；C.圆锥的主视图是等腰三角形，俯视图是圆，故该选项符合题意；D.球的主视图与俯视图都是圆，故该选项不符合题意；故答案为：C.
【分析】分别确定各几何体的主视图与俯视图，再判断即可.5．【答案】B【解析】【解答】解：由题意得：，∥，∴，∵，，∴，∴，故答案为：B.【分析】由题意可得∠1=78°，AE∥GH，根据平行线的性质可得∠HFC=∠1=78°，由余角的性质可得∠C=90°-∠BDC=30°，根据外角的性质可得∠2+∠C=∠HFC，据此计算.6．【答案】C【解析】【解答】解：设工程队提高工作效率后的解析式为：，把，分别代入解析式，得：解得，当时，，则该工程队提高效率前每天修路的长度是：(米)，故答案为：C．
【分析】先利用待定系数法求出一次函数解析式，再求解即可。7．【答案】A【解析】【解答】解：∵各三角形都是等腰直角三角形，∴直角顶点的纵坐标的长度为斜边的一半，，，…，∵余3，∴点在x轴负半轴，横坐标是.故答案为：A.【分析】根据等腰直角三角形的性质可得：直角顶点的纵坐标的长度为斜边的一半，表示出A3、A7、A11的坐标，求出2023÷4的商与余数，进而可得点A2023的横坐标.8．【答案】B【解析】【解答】解：设等腰直角三角形的直角边为，正方形边长为，则，，，平行四边形面积.故答案为：B.【分析】设等腰直角三角形的直角边为a，正方形边长为c，根据正方形的性质以及三角形的面积公式可得S2=(a+c)(a-c)=a2-c2，结合正方形的面积公式可得S3=2S1-2S2，进而推出平行四边形的面积=2S1+2S2+S3=4S1，据此求解.9．【答案】C【解析】【解答】解：由题意知，小于20的所有质数为2，3，5，7，11，13，17，19，共计8个，从中一次性抽取2个共计有28种等可能结果，其中满足这两个数作差并取绝对值后得到的新的数仍为质数的组合有，，，，，，，共计8种情况，∴概率，故答案为：C．【分析】根据题意先求出从中一次性抽取2个共计有28种等可能结果，再求概率即可。10．【答案】D【解析】【解答】解：当时，，则， 当时，，解得，则，，，设，当时，面积的最大值为4．故答案为：D．
【分析】设，求出，再利用二次函数的性质求解即可。11．【答案】x≤2【解析】【解答】解：，移项合并得：，化系数为1得：x≤2，故答案为：x≤2．
【分析】利用不等式的性质及不等式的解法求出解集即可。 12．【答案】2＜x≤4【解析】【解答】解：由题意得，4-x≥0且x-2＞0，解得2＜x≤4，故答案为：2＜x≤4.
【分析】二次根式有意义条件：被开方数为非负数；分式有意义的条件：分母不为0，据此解答即可.13．【答案】27°【解析】【解答】解：如图所示，连接，∵是的切线，∴，∵，∴，∴，故答案为：.【分析】连接OC，由切线的性质可得∠OCD=90°，结合内角和定理可得∠DOC=54°，由圆周角定理可得∠A=∠DOC，据此计算.14．【答案】【解析】【解答】解：如图，取AB的中点O，连接OG，延长CD到T，使得DT=CD，连接OT，PT，TG，过点O作OH⊥CD于H. ∵四边形ABCD是正方形，∴，∴，∵，∴，∴，∵，，，∴，∴，∵，∴，∴，∵，∴，在中，，∴，∴，∴，∴的最小值为，故答案为：. 【分析】取AB的中点O，连接OG，延长CD到T，使DT=CD，连接OT，PT，TG，过点O作OH⊥CD于H，易得PD是CT的垂直平分线，故PT=PC，则PG+PC=PG+PT≥GT；由SAS证出△BAE≌△ADF，得∠ABE=∠DAF，由角的和差及等量代换得∠AGB=90°，由直角三角形斜边上的中线等于斜边的一半得OG=AB=2，在Rt△OHT中，由勾股定理算出OT，由三角形三边关系得GT≥OT-OG，据此即可得出答案.15．【答案】解：.【解析】【分析】根据有理数的乘方法则、负整数指数幂的运算性质、特殊角的三角函数值以及绝对值的性质可得原式=-1+2-2×+-1，然后计算乘法，再根据二次根式的加法法则以及有理数的加减法法则进行计算.16．【答案】解：⑴如图，即为所求；⑵如图，即为所求．【解析】【分析】（1）利用旋转的性质找出点A、B、C的对应点，再连接即可；
（2）利用平移的性质找出点A、B、C的对应点，再连接即可。17．【答案】解：过A作交延长线于E， 由题意，得，，，在中，，在中，，则，解得，∵，∴渔船不改变航线继续向东航行，没有触礁的危险．【解析】【分析】过A作交延长线于E，先求出，，再列出方程，求出，最后比较大小即可。18．【答案】解：（1）第一行数是−1，2，−3，4，−5，…，即（−1）nn；
（2）对于一、二两行中位置对应的数，可以发现：第二行数是与第一行数的每一个相对应的数的平方，第三行每一个数是第二行对应的数减1得到的，即为第一行数的每一个相对应的数的平方减1得到；
（3）根据规律得出：第一行数第10个数为10，第二行数第10个数为100，第三行数第10个数为99，则这三个数的和为：10＋100＋99＝209．【解析】【分析】（1）观察第一行数可知：第奇数个数为负，第偶数个数为正，其每一个数的绝对值是连续自然数；
（2）观察第二行数可知：每一个数依次是对应的第一行数的平方；观察第二行数可知：第三行每一个数是第二行对应的数减1得到的，即为第一行数的每一个相对应的数的平方减1得到；
（3）根据（1）（2）的规律可求解.19．【答案】（1）解：，，反比例函数为①，设直线OA解析式为，将代入得，，，直线OA解析式为②，由①②得，不合题意，舍去，，为（2）解：将代入，得，点D的坐标为，点在该反比例函数图象上，且在的内部包含边界，且C的坐标为，由图象得【解析】【分析】（1）根据反比例函数系数k的几何意义可得S△OBD==2，求解可得k的值，据此可得反比例函数的解析式；设直线OA的解析式为y=mx，将A（4，4）代入求出m的值，得到直线OA的解析式，联立反比例函数的解析式可得x、y的值，据此可得点C的坐标；
（2）将x=4代入反比例函数解析式中求出y的值，得到点D的坐标，然后结合图象可得b的范围.20．【答案】（1）证明：连接，∵与相切于点C，∴，∴，∵，∴，∴，∵，∴，∴，∴是等腰三角形，∴；（2）解：∵为直径，∴，在中，，，∴，∵平分，∴，∵，∴，∴.【解析】【分析】（1）连接OC，根据切线的性质可得OC⊥CD，则∠COD=90°-∠D=60°，结合等腰三角形的性质以及外角的性质可得∠OCA=∠OAC=30°，推出△ACD为等腰三角形，据此证明；
（2）由圆周角定理可得∠ACB=90°，根据含30°角的直角三角形的性质可得BC=AB=6，由角平分线的概念可得∠ECB=∠ACB=45°，然后根据三角函数的概念进行计算.21．【答案】（1）60（2）解：选择C的人数为：，补全条形统计图如下：（3）解：该校最想去森林公园的学生人数大约为：(人)，答：估计该校最想去森林公园的学生人数为720人；（4）解：画树状图如下：共有16种等可能的结果，其中和为5的结果有4种，因此小军获胜的概率为．【解析】【解答】（1）解：本次调查的样本容量是：；
【分析】（1）根据样本容量的定义计算求解即可；
（2）先求出选择C的人数为23名，再补全条形统计图即可；
（3）根据该学校共有3600名学生， 计算求解即可；
（4）先画树状图，再求出共有16种等可能的结果，其中和为5的结果有4种，最后求概率即可。22．【答案】（1）解：由题意得：，∴宾馆每天的营业额y与房价x的函数关系式为（2）解：∵，∴当时，W最大，最大值为10890，答：房价定为350元时，宾馆利润W最大．【解析】【分析】（1）根据题意直接列出函数解析式即可；
（2）根据题意列出函数解析式，再利用二次函数的性质求解即可。23．【答案】（1）等腰直角三角形；（2）解：①成立，理由如下，如图连接，当时，，，，，，，，是等腰直角三角形，，，，在中，，，同理，在中，，，，，故结论成立；②存在，【解析】【解答】（1）解：如图，连接，当时，，，，是等边三角形，，，，，，是等腰直角三角形，，，，在中，，，同理，在中，，，，，故答案为：等腰直角三角形，；（2）②如图，当时，，，，由①可知，，，，同理可证，，，，，，，，，，，，，，，，是等腰直角三角形，，，，，，，，在中，，由①可知，，，，在中，，，．【分析】（1）先求出△BEF是等腰直角三角形，再利用相似三角形的判定与性质计算求解即可；
（2）①先求出∠FBE=45°，再利用勾股定理和相似三角形的判定与性质计算求解即可；
②先求出，再求出，最后利用勾股定理计算求解即可。