中考数学三轮冲刺《二次函数压轴题》强化练习一（含答案）

这是一份中考数学三轮冲刺《二次函数压轴题》强化练习一（含答案），共15页。
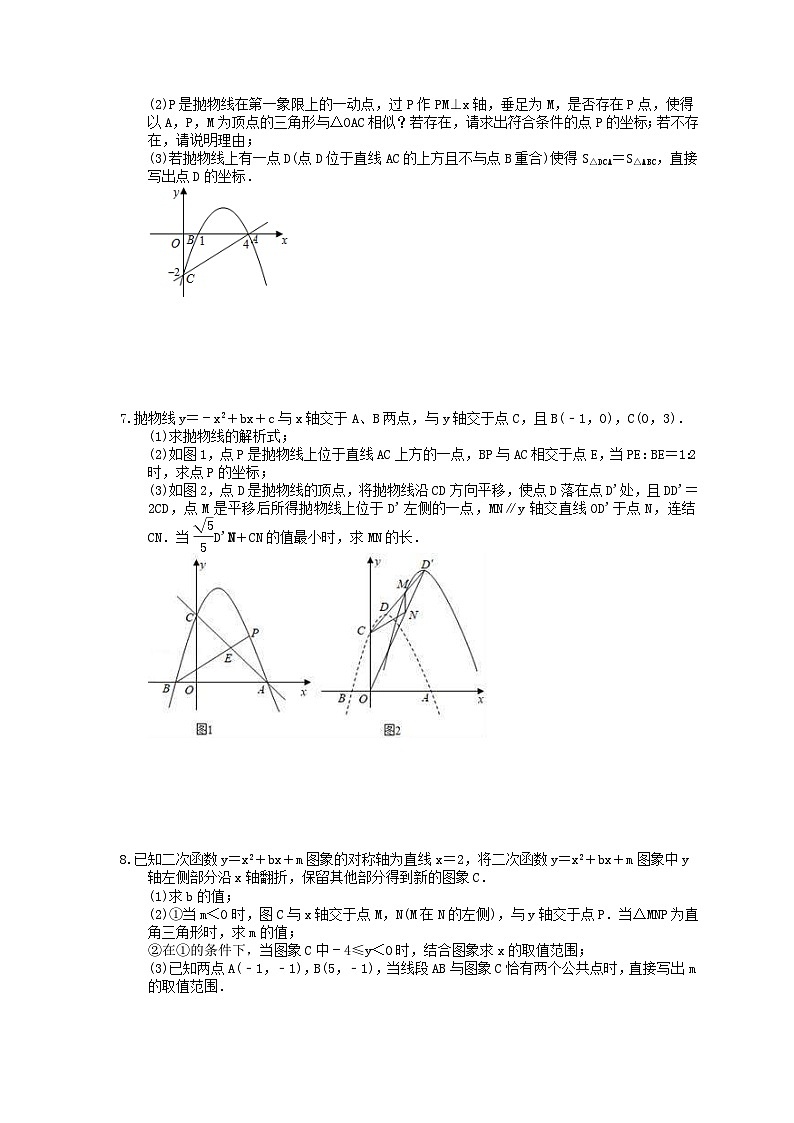
中考数学三轮冲刺《二次函数压轴题》强化练习一1.如图，以直线x=1为对称轴的抛物线y=ax2＋bx＋c(a，b，c为常数)经过A(4，0)和B(0，4)两点，其顶点为C．(1)求该抛物线的解析式及其顶点C的坐标；(2)若点M是抛物线上的一个动点，且位于第一象限内．①设△ABM的面积为S，试求S的最大值；②若S为整数，则这样的M点有     个．       2.抛物线y1＝ax2﹣2ax＋c(a＜2且a≠0)与x轴交于A(﹣1，0)，B两点，抛物线的对称轴与x轴交于点D，点M(m，n)在该抛物线上，点P是抛物线的最低点．(1)若m＝2，n＝﹣3，求a的值；(2)记△PMB面积为S，证明：当1＜m＜3时，S＜2；(3)将直线BP向上平移t个单位长度得直线y2＝kx＋b(k≠0)，与y轴交于点C，与抛物线交于点E，当x＜﹣1时，总有y1＞y2．当﹣1＜x＜1时，总有y1＜y2．是否存在t≥4，使得△CDE是直角三角形，若存在，求t的值；若不存在，请说明理由．      3.如图，抛物线y＝ax2＋2x＋c的对称轴是直线x＝1，与x轴交于点A，B(3，0)，与y轴交于点C，连接AC．(1)求此抛物线的解析式；(2)已知点D是第一象限内抛物线上的一个动点，过点D作DM⊥x轴，垂足为点M，DM交直线BC于点N，是否存在这样的点N，使得以A，C，N为顶点的三角形是等腰三角形．若存在，请求出点N的坐标，若不存在，请说明理由；(3)已知点E是抛物线对称轴上的点，在坐标平面内是否存在点F，使以点B、C、E、F为顶点的四边形为矩形，若存在，请直接写出点F的坐标；若不存在，请说明理由．      4.在平面直角坐标系xOy中，已知抛物线y＝﹣x2＋2kx＋2k2＋1与x轴的左交点为A，右交点为B，与y轴的交点为C，对称轴为直线l，对于抛物线上的两点(x1，y1)，(x2，y2)(x1＜k＜x2)，当x1＋x2＝2时，y1﹣y2＝0恒成立．(1)求该抛物线的解析式；(2)点M是第二象限内直线AC上方的抛物线上的一点，过点M作MN⊥AC于点N，求线段MN的最大值，并求出此时点M的坐标；(3)点P是直线l右侧抛物线上的一点，PQ⊥l于点Q，AP交直线l于点F，是否存在这样的点P，使△PQF与△ACO相似？若存在，请求出点P的坐标，若不存在，请说明理由．      5.如图，在平面直角坐标系xOy中，抛物线y＝ax2＋bx＋6与x轴交于点A(﹣2，0)和点B(6，0)，与y轴交于点C，顶点为D，联结BC交抛物线的对称轴l于点E．(1)求抛物线的表达式；(2)联结CD、BD，点P是射线DE上的一点，如果S△PDB＝S△CDB，求点P的坐标；(3)点M是线段BE上的一点，点N是对称轴l右侧抛物线上的一点，如果△EMN是以EM为腰的等腰直角三角形，求点M的坐标．      6.如图，抛物线经过A(4，0)，B(1，0)，C(0，﹣2)三点．(1)求出抛物线的解析式；(2)P是抛物线在第一象限上的一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；(3)若抛物线上有一点D(点D位于直线AC的上方且不与点B重合)使得S△DCA＝S△ABC，直接写出点D的坐标．      7.抛物线y＝﹣x2＋bx＋c与x轴交于A、B两点，与y轴交于点C，且B(﹣1，0)，C(0，3)．(1)求抛物线的解析式；(2)如图1，点P是抛物线上位于直线AC上方的一点，BP与AC相交于点E，当PE：BE＝1：2时，求点P的坐标；(3)如图2，点D是抛物线的顶点，将抛物线沿CD方向平移，使点D落在点D'处，且DD'＝2CD，点M是平移后所得抛物线上位于D'左侧的一点，MN∥y轴交直线OD'于点N，连结CN．当D'N＋CN的值最小时，求MN的长．      8.已知二次函数y＝x2＋bx＋m图象的对称轴为直线x＝2，将二次函数y＝x2＋bx＋m图象中y轴左侧部分沿x轴翻折，保留其他部分得到新的图象C．(1)求b的值；(2)①当m＜0时，图C与x轴交于点M，N(M在N的左侧)，与y轴交于点P．当△MNP为直角三角形时，求m的值；②在①的条件下，当图象C中﹣4≤y＜0时，结合图象求x的取值范围；(3)已知两点A(﹣1，﹣1)，B(5，﹣1)，当线段AB与图象C恰有两个公共点时，直接写出m的取值范围．      
0.中考数学三轮冲刺《二次函数压轴题》强化练习一（含答案）答案解析  一         、综合题1.解：(1)∵抛物线的对称轴为直线x=1，抛物线与x轴的一个交点为A(4，0)，∴抛物线与x轴的另一个交点为(﹣2，0)，设抛物线的解析式为y=a(x＋2)(x﹣4)，把B(0，4)代入得a•2•(﹣4)=4，解得a=﹣，∴抛物线的解析式为y=﹣(x＋2)(x﹣4)，即y=﹣x2＋x＋4；∵y=﹣(x﹣1)2＋，∴抛物线的顶点C的坐标为(1，)；(2)①过M点作MN∥y轴交AB于N点，如图，设AB的解析式为y=mx＋n，把B(0，4)、A(4，0)代入得，解得，∴直线AB的解析式为y=﹣x＋4，设M(t，﹣t2＋t＋4)，则N(t，﹣t＋4)，∴MN=﹣t2＋t＋4﹣(﹣t＋4)=﹣t2＋2t，∴S=S△BMN＋S△AMN=•4•MN=•4•(﹣t2＋2t)=﹣t2＋4t=﹣(t﹣2)2＋4，∴当t=2时，S有最大值，最大值为4；②∵0＜t＜4，∴当t=1、2、3时，S为整数，即这样的M点有3个．故答案为3． 2.解：(1)将点A(﹣1，0)代入抛物线y1＝ax2﹣2ax＋c中，∴a＋2a＋c＝0，∴c＝﹣3a，∴抛物线y1＝ax2﹣2ax﹣3a．当m＝2，n＝﹣3时，M(2，﹣3)，∴4a﹣4a﹣3a＝﹣3，解得a＝1；(2)证明：过点M作x轴的垂线，交直线BP于点Q，∵点P为y1＝ax2﹣2ax﹣3a的最低点，∴P(a，﹣4a)，令y1＝ax2﹣2ax﹣3a＝0，解得x＝﹣1或x＝3，∴B(3，0)，∴直线BP的解析式为：y＝2ax﹣6a，设M(m，am2﹣2am﹣3a)，∴Q(m，2am﹣6a)，∴QM＝2am﹣6a﹣(am2﹣2am﹣3a)＝﹣am2＋4am﹣3a，∴S＝|xB﹣xP|•QM＝﹣am2＋4am﹣3a＝﹣a(m﹣2)2＋a，∵﹣a＜0，开口向下，∴当m＝2时，S的最大值为a，∵a＜2，∴当1＜m＜3时，S＝a＜2．(3)解：∵当x＜﹣1时，总有y1＜y2，∴直线l必经过点A(﹣1，0)，将点A代入直线l：y2＝kx＋b，∴﹣k＋b＝0，∵直线l：y2＝kx＋b由直线PB：y＝2ax﹣6a向上平移t个单位长度得到，∴k＝b＝2a，b＝﹣6a＋t＝2a，∴t＝8a，∴y2＝2ax＋2a，点C(0，2a)，令2ax＋2a＝ax2﹣2ax﹣3a，解得x＝﹣1或x＝5，∴E(5，12a)．①当∠ECD＝90°时，过点E作y轴的垂线交y轴于点F，∴△FEC∽△OCD，∴EF：OC＝CF：OD，即5：2a＝10a：1，∴a＝或a＝﹣(舍)；∴t＝8a＝4≥4，符合题意；②当∠CDE＝90°时，过点E作x轴的垂线于点F，∴△OCD∽△FDE，∴EF：OD＝DF：OC，即12a：1＝4：2a，解得a＝或a＝﹣(舍)，∴t＝8a＝＜＝4，不符合题意；③当∠CED＝90°时，显然不存在．综上，存在，且t的值为． 3.解：(1)抛物线y＝ax2＋2x＋c的对称轴是直线x＝1，与x轴交于点A，B(3，0)，∴A(﹣1，0)，∴，解得，∴抛物线的解析式y＝﹣x2＋2x＋3；(2)∵y＝﹣x2＋2x＋3，∴C(0，3)，设直线BC的解析式为y＝kx＋3，将点B(3，0)代入得：0＝3k＋3，解得：k＝﹣1，∴直线BC的解析式为y＝﹣x＋3；设点D坐标为(t，﹣t2＋2t＋3)，则点N(t，﹣t＋3)，∵A(﹣1，0)，C(0，3)，∴AC2＝12＋32＝10，AN2＝(t＋1)2＋(﹣t＋3)2＝2t2﹣4t＋10，CN2＝t2＋(3＋t﹣3)2＝2t2，①当AC＝AN时，AC2＝AN2，∴10＝2t2﹣4t＋10，解得t1＝2，t2＝0(不合题意，舍去)，∴点N的坐标为(2，1)；②当AC＝CN时，AC2＝CN2，∴10＝2t2，解得t1＝，t2＝﹣ (不合题意，舍去)，∴点N的坐标为(，3﹣)；③当AN＝CN时，AN2＝CN2，∴2t2﹣4t＋10＝2t2，解得t＝，∴点N的坐标为(，)；综上，存在，点N的坐标为(2，1)或(，3﹣)或(，)；(3)设E(1，a)，F(m，n)，∵B(3，0)，C(0，3)，∴BC＝3，①以BC为对角线时，BC2＝CE2＋BE2，∴(3)2＝12＋(a﹣3)2＋a2＋(3﹣1)2，解得：a＝＋，或a＝﹣，∴E(1，＋)或(1，﹣)，∵B(3，0)，C(0，3)，∴m＋1＝0＋3，n＋＋＝0＋3或n＋﹣＝0＋3，∴m＝2，n＝﹣或n＝＋，∴点F的坐标为(2，﹣)或(2，＋)；②以BC为边时，BE2＝CE2＋BC2或CE2＝BE2＋BC2，∴a2＋(3﹣1)2＝12＋(a﹣3)2＋(3)2或12＋(a﹣3)2＝a2＋(3﹣1)2＋(3)2，解得：a＝4或a＝﹣2，∴E(1，4)或(1，﹣2)，∵B(3，0)，C(0，3)，∴m＋0＝1＋3，n＋3＝0＋4或m＋3＝1＋0，n＋0＝3﹣2，∴m＝4，n＝1或m＝﹣2，n＝1，∴点F的坐标为(4，1)或(﹣2，1)，综上所述：存在，点F的坐标为(2，﹣)或(2，＋)或(4，1)或(﹣2，1)． 4.解：(1)∵(x1，y1)，(x2，y2)在抛物线y＝﹣x2＋2kx＋2k2＋1上，∴x1＋x2＝2k，x1x2＝﹣2k2﹣1，y1＝﹣x12＋2kx1＋2k2＋1，y2＝﹣x22＋2kx2＋2k2＋1，∴y1﹣y2＝(﹣x12＋2kx1＋2k2＋1)﹣(﹣x22＋2kx2＋2k2＋1)＝(x2﹣x1)(x1＋x2﹣2k)，∵当x1＋x2＝2时，y1﹣y2＝0恒成立，∴(x2﹣x1)(2﹣2k)＝0，∵x1＜k＜x2，∴2﹣2k＝0，∴k＝1，∴该抛物线的解析式为y＝﹣x2＋2x＋3；(2)由(1)知：y＝﹣x2＋2x＋3，令y＝0，得﹣x2＋2x＋3＝0，解得：x1＝﹣1，x2＝3，∴A(﹣1，0)，B(3，0)，令x＝0，得y＝3，∴C(0，3)，在Rt△AOC中，AC＝＝，设直线AC的解析式为y＝mx＋n，则，解得：，∴直线AC的解析式为y＝3x＋3，如图1，过点M作MD∥y轴交AC于点D，设M(t，﹣t2＋2t＋3)(﹣1＜t＜0)，则D(t，3t＋3)，∴MD＝﹣t2＋2t＋3﹣(3t＋3)＝﹣t2﹣t，∵MN⊥AC，∴∠MND＝90°＝∠AOC，∵MD∥OC，∴∠MDN＝∠ACO，∴△MDN∽△ACO，∴＝，即＝，∴MN＝﹣(t＋)2＋，∵﹣＜0，∴当t＝﹣时，线段MN取得最大值，此时，M(﹣，)；(3)存在．∵y＝﹣x2＋2x＋3＝﹣(x﹣1)2＋4，∴抛物线的对称轴为直线x＝1，设P(m，﹣m2＋2m＋3)(m＞1)，则Q(1，﹣m2＋2m＋3)，过点P作PH⊥x轴于点H，则H(m，0)，∵PQ⊥l，l⊥x轴，∴PQ∥x轴，∴∠FPQ＝∠PAH，∵∠PQF＝∠AHP，∴△PFQ∽△APH，当点P在x轴上方时，如图2，PH＝﹣m2＋2m＋3，AH＝m＋1，又OA＝1，OC＝3，若△PFQ∽△CAO，则△APH∽△CAO，∴＝，即＝，解得：m＝﹣1(舍去)或m＝，当m＝时，﹣m2＋2m＋3＝﹣()2＋2×＋3＝，∴P(，)；若△PFQ∽△ACO，则△APH∽△ACO，∴＝，即＝，解得：m＝﹣1(舍去)或m＝0(不符合题意，舍去)；当点P在x轴下方时，如图3，PH＝m2﹣2m﹣3，AH＝m＋1，若△PFQ∽△CAO，则△APH∽△CAO，∴＝，即＝，解得：m＝﹣1(舍去)或m＝，当m＝时，﹣m2＋2m＋3＝﹣()2＋2×＋3＝﹣，∴P(，﹣)；若△PFQ∽△ACO，则△APH∽△ACO，∴＝，即＝，解得：m＝﹣1(舍去)或m＝6，当m＝6时，﹣m2＋2m＋3＝﹣62＋2×6＋3＝﹣21，∴P(6，21)；综上所述，点P的坐标为(，)或(，﹣)或(6，21)． 5.解：(1)将A(﹣2，0)，B(6，0)代入y＝ax2＋bx＋6，得：，解得：，∴二次函数的解析式为y＝﹣x2＋2x＋6；(2)如图：∵y＝﹣x2＋2x＋6＝﹣(x﹣2)2＋8，∴C(0，6)、D(2，8)，∵B(6，0)，∴BC＝6，CD＝2，BD＝4，∴BC2＋CD2＝BD2，∴△BCD是直角三角形，∠BCD＝90°，∴S△BCD＝BC•CD＝12，∵S△PDB＝PD•(6﹣2)＝2PD＝S△CDB＝12，∴PD＝6，∴P(2，2)；(3)∵B(6，0)，C(0，6)．∴直线BC的解析式为y＝﹣x＋6，OB＝OC，∴∠OBC＝∠OCB＝45°，∵y＝﹣x2＋2x＋6，∴对称轴l为x＝2，当x＝2时，y＝﹣x＋6＝4，∴E(2，4)，设M(m，﹣m＋6)，且2＜m＜6，①当∠MEN＝90°，EM＝EN时，过点E作EH⊥MN于H，∴MN＝2EH，∠EMN＝∠ENM＝45°，∵∠OBC＝∠OCB＝45°，∴∠NME＝∠OCB，∴MN∥y轴，∴N(m，﹣m2＋2m＋6)，∴MN＝﹣m2＋2m＋6＋m﹣6＝﹣m2＋3m，EH＝m﹣2，∴﹣m2＋3m＝2(m﹣2)，解得m＝4或m＝﹣2(不合题意，舍去)，∴M(4，2)；②当∠EMN＝90°，EM＝MN时，∴EH＝NH＝MH＝EN，∠MEN＝∠ENM＝45°，∵∠OBC＝∠OCB＝45°，∴∠MEN＝∠OBC，∴EN∥x轴，∴点N的纵坐标为4，当y＝4时，﹣x2＋2x＋6＝4，解得x＝2＋2或x＝2﹣2(不合题意，舍去)，∴N(2＋2，4)，∴EN＝2＋2﹣2＝2，∴EH＝MH＝EN＝，∴m＝2＋，∴M(2＋，4﹣)；综上所述，点M的坐标为(4，2)或(2＋，4﹣)． 6.解：(1)设抛物线的解析式为y＝ax2＋bx＋c，将A(4，0)，B(1，0)，C(0，﹣2)代入y＝ax2＋bx＋c，∴，解得，∴y＝﹣x2＋x﹣2；(2)存在P点，使得以A，P，M为顶点的三角形与△OAC相似，理由如下：设P(t，﹣t2＋t﹣2)，则M(t，0)，1＜t＜4，∴PM＝﹣t2＋t﹣2，∵A(4，0)，∴AM＝4﹣t，∴tan∠MAP＝，∵C(0，﹣2)，∴OC＝2，OA＝4，∴tan∠OAC＝，①当∠PAM＝∠OAC时，＝，解得t＝2或t＝4(舍)，∴P(2，1)；②当∠PAM＝∠OCA时，＝2，解得t＝4(舍)或t＝5(舍)，∴此时P不存在；综上所述：P点坐标为(2，1)；(3)设直线AC的解析式为y＝kx＋b，∴，∴，∴直线AC的解析式为y＝x﹣2，过点B作直线AC的平行线y＝x＋m，∴＋m＝0，∴m＝﹣，∴y＝x﹣，联立方程组，解得(舍)或，∴D(3，1)． 7.解：(1)∵y＝﹣x2＋bx＋c经过B(﹣1，0)，C(0，3)，∴，解得，∴抛物线的解析式为y＝﹣x2＋2x＋3．(2)如图1中，过点B作BT∥y轴交AC于T，过点P作PQ∥OC交AC于Q．设P(m，﹣m2＋2m＋3)，对于抛物线y＝﹣x2＋2x＋3，令y＝0，可得x＝3或﹣1，∴A(3，0)，∵C(0，3)，∴直线AC的解析式为y＝﹣x＋3，∵B(﹣1，0)，∴T(﹣1，4)，∴BT＝4，∵PQ∥OC，∴Q(m，﹣m＋3)，∴PQ＝﹣m2＋2m＋3﹣(﹣m＋3)＝﹣m2＋3m，∵PQ∥BT，∴＝＝，∴﹣m2＋3m＝2，解得m＝1或2，∴P(1，4)或(2，3)．(3)如图2中，连接AD′，过点N作NJ⊥AD′于J，过点C作CT⊥AD′于T．∵抛物线y＝﹣x2＋2x＋3＝﹣(x﹣1)2＋4，∴顶点D(1，4)，∵C(0，3)，∴直线CD的解析式为y＝x＋3，CD＝，∵DD′＝2CD，∵DD′＝2，CD′＝3，∴D′(3，6)，∵A(3，0)，∴AD′⊥x轴，∴OD′＝3，∴sin∠OD′A＝，∵CT⊥AD′，∴CT＝3，∵NJ⊥AD′，∴NJ＝ND′sin∠OD′A＝D′N，∴D'N＋CN＝CN＋NJ，∵CN＋NJ≥CT，∴D'N＋CN≥3，∴D'N＋CN的最小值为3，此时N为OD'与CT的交点，∴N(1.5，3)，∵平移后抛物线的解析式为y＝﹣(x﹣3)2＋6，MN平行y轴，将x＝1.5代入抛物线解析式，∴M(，)，∴MN＝. 8.解：(1)∵已知二次函数y＝x2＋bx＋m图象的对称轴为直线x＝2，∴b＝﹣4；(2)如图1：①令x2＋bx＋m＝0，解得x＝2﹣或x＝2＋，∵M在N的左侧，∴M(2﹣，0)，N(2＋，0)，∴MN＝2，MN的中点坐标为(2，0)，∵△MNP为直角三角形，∴＝，解得m＝0(舍)或m＝﹣1；②∵m＝﹣1，∴y＝x2﹣4x﹣1(x≥0)，令x2﹣4x﹣1＝﹣4，解得x＝1或x＝3，∴抛物线y＝x2﹣4x﹣1(x≥0)与直线y＝﹣4的交点为(1，﹣4)，(3，﹣4)，∵y＝x2﹣4x﹣1关于x轴对称的抛物线解析式为y＝﹣x2＋4x＋1(x＜0)，当﹣x2＋4x＋1＝﹣4时，解得x＝5(舍)或x＝﹣1，∴抛物线y＝﹣x2＋4x＋1(x＜0)与直线y＝﹣4的交点为(﹣1，﹣4)，∴﹣1≤x＜2﹣或0≤x≤1或3≤x＜2＋时，﹣4≤y＜0；(3)y＝x2﹣4x＋m关于x轴对称的抛物线解析式为y＝﹣x2＋4x﹣m(x＜0)，如图2，当y＝﹣x2＋4x﹣m(x＜0)经过点A时，﹣1﹣4﹣m＝﹣1，解得m＝﹣4，∴y＝x2﹣4x﹣4(x≥0)，当x＝5时，y＝1，∴y＝x2﹣4x﹣4(x≥0)与线段AB有一个交点，∴m＝﹣4时，当线段AB与图象C恰有两个公共点；如图3，当y＝x2﹣4x＋m(x≥0)经过点(0，﹣1)时，m＝﹣1，此时图象C与线段AB有三个公共点，∴﹣4≤m＜﹣1时，线段AB与图象C恰有两个公共点；  如图4，当y＝﹣x2＋4x﹣m(x＜0)经过点(0，﹣1)时，m＝1，此时图象C与线段AB有两个公共点，当y＝x2﹣4x＋m(x≥0)的顶点在线段AB上时，m﹣4＝﹣1，解得m＝3，此时图象C与线段AB有一个公共点，∴1≤m＜3时，线段AB与图象C恰有两个公共点；综上所述：﹣4≤m＜﹣1或1≤m＜3时，线段AB与图象C恰有两个公共点．